б) Понятие средней квадратической ошибки. Оценка точности измерений по формуле К. Гаусса

 Чтобы выполнить оценку точности измерений, необходимо оценить прежде всего точность отдельного измерения. Казалось бы естественным взять для этого среднее арифметическое из всех случайных ошибок. Однако при этом на величину средней ошибки влияли бы разные знаки отдельных ошибок и может случиться так, что ряд с крупными отдельными ошибками получил бы меньшую среднюю ошибку, чем ряд с меньшими ошибками.

Если взять среднее арифметическое из абсолютных значений случайных ошибок, то при этом не будет достаточно отражено наличие в данном ряде отдельных сравнительно крупных ошибок.

При выборе критерия для оценки точности ряда измерений необходимо иметь в виду, что результат должен быть одинаково ошибочным, будет ли он больше или меньше истинного значения измеряемой величины. Кроме того, чем крупнее в данном ряде отдельные ошибки, тем меньше должна быть его точность.

Этим условиям лучше всего удовлетворяет средняя квадратическая ошибка результата измерения, выражаемая соотношением

                       m =  ,                ( 8 )

где 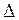_i - разности измеренных величин  l _i и истинных значений X

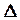                                  _i = l  _i - X ,                          ( 9 )

известным как формула К . Гаусса

Пример обработки результатов измерения длины линии представлен в таблице 1.

Таблица 1 Обработка результатов измерения длины линии по формуле К. Гаусса

                     №№       Измеренная   Истинная Ошибки

                  измере-   длина           длина      _i,см  _i²,см

                   ний           l _i ,м                        X, м

1          110.01            110.01          0        0

2                03                                   + 2        4

3               02                                    +1        1

4                05                                    +4      16

5              04                                    +3        9

                                                                                        = 30

                                             m = 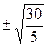= 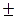2.45 см.

Утроенное значение ср.кв.ош. принимается в качестве предельной ошибки D _пр = 3m при вероятности р = 0.997. При вероятности р = 0.99 предельная ошибка D _пр = 2.5 m, а при вероятности р = 0.95 D _пр. = 2 m

в) Оценка точности измерений по формуле Ф. Бесселя                           ( по вероятнейшим уклонениям )

При выполнении измерений истинное значение измеряемой величины, как правило, неизвестно. В этом случае ср.кв.ош. отдельного измерения вычисляют по вероятнейшим уклонениям V измеренных величин от их среднего арифметического .

Формулу для оценки результатов измерений по вероятнейшим уклонениям вывел немецкий астроном Ф. Бессель, которая представляется в виде

               m = 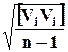  = ,           ( 10 )

где V_i - уклонение отдельных измерений   l _i от их среднего арифметического  l _ср ( V_i  = l _i - l _ср  );

n      - число измерений.

Среднюю квадратическую ошибку М среднего результата измерения

 в этом случае вычисляют по формуле

                       М = .                            ( 11 )

  Пример обработки результатов измерения длины линии приводится в таблице 2.

Таблица 2 Обработка результатов измерений по формуле Ф. Бесселя

                            № №              Измеренная

                    измерений           величина,     V _{i ,} см  V² _i, см

                                                      l _{i ,} м

                          1                 125.10              0         0

                          2                 125.12           + 2         4

                          3                 125.08           - 2             4

                          4                 125.08           - 2         4

                          5                 125.12           + 2       4   

                       n = 5            l ср = 125.10 м =0   =16

                                           m = 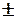  2 см , М =  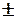  0.9 см.

д) Оценка точности измерений по разностям двойных измерений

При выполнении топографо-геодезических работ одну и ту же величину часто измеряют дважды. Например, длины сторон теодолитного хода измеряют землемерной лентой прямо и обратно, горизонтальные углы - двумя полуприёмами и т.д. В этом случае оценку точности результатов измерений выполняют по разностям двойных измерений. При этом, если оценивают точность определения одной разности из всей совокупности измерений, то вычисляют её среднюю квадратическую   ошибку m _{d i}   из соотношения, близкого по своему смыслу к формуле К. Гаусса, т.к. истинные ошибки разностей равны нулю

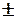
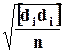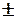
                    m _{d i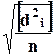} =  = ,               ( 12 )

 где d _i   - разности двойных измерений   l _{1 ,} l _;

n    - число двойных разностей .

Каждая разность образована как d _i  = l ₁ - l ₂. Поэтому ср.кв.ош. одной разности d   выражается формулой m ² _d  = m ² _l  + m²₂ . Так как измерения l  равноточны, то m _l = m ₂  = m _l . Следовательно,  m² _d  = 2 m² _l. Отсюда m _d = m _l 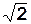, а 

                              m _l = m _d / 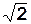 .                           ( 13 )

Подставив в формулу ( 12 ) соотношение для m _d ( 11 ) , получим выражение для ср.кв.ош.. m _l  отдельного измерения l_i по разностям двойных измерений

                             m _{l i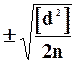}  = .                        ( 14 )

Из разности двойных измерений l ₁ и  l ₂    обычно берут среднее значение  

                                  l ср. = 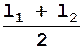,                         ( 15 )

тогда согласно формуле ( 13 )

                                                 m _{l ср.} = .                            ( 16 )

Подставляя в формулу ( 16 ) выражение ( 14 ) для  m _l , получим формулу для оценки точности среднего арифметического из всей совокупности измерений по разностям двойных измерений

                                m _{l ср.} = .                       ( 17 )

Приведенные формулы ( 12 ), ( 14 ), ( 17 ) справедливы для случая, когда разности двойных измерений являются случайными ошибками ( свободны от систематических ошибок ), т.е. тогда, когда выражение 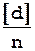 = 0 или близко к нулю. Если это выражение заметно отличается от нуля, то формулы, приведенные выше для оценки точности результатов измерений по разностям двойных измерений, применять нельзя.

В этом случае необходимо определить систематическую ошибку   по формуле

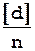                      =                                ( 18 )

и исключить её из каждой разности двойных измерений, вычислив величины  по формуле

                                = d _i  - .                     ( 19 )

Значения ошибок  являются по существу уклонениями разностей d _i  от их арифметической средины , т.е. являются вероятнейшими ошибками. Следовательно, для оценки точности измерений по результатам двойных измерений может быть применена формула Бесселя.

В этом случае ср.кв.ош. определения одной разности m _{d i} из всей совокупности двойных измерений определяют по формуле

                          m _{d i} = .                             ( 20 )

Средние квадратические ошибки определения отдельного результата измерения m _{l i}    и   среднего арифметического m _{l ср.}  из всей совокупности измерений вычисляют из соотношений

                                m _li =  ,                        ( 21 )

                              m _{l ср.}  = .                     ( 22 )