Элементы теории ошибок измерений
Оценка точности равноточных измерений
Измерения, выполненные в одинаковых условиях, равным числом приёмов измерений, одним и тем же прибором называют равноточными.
а) Понятие точности измерений, арифметической средины
Под точностью измерений понимают качество измерений, определяющее близость их результатов к точному значению измеряемой величины.
В какой последовательности выполняют оценку точности результатов равноточных измерений?
Её выполняют в следующей последовательности:
- вычисляют значение арифметической средины X ( среднего арифметического ) ;
- вычисляют значение средней квадратической ошибки ( ср. кв.ош. ) m отдельного измерения;
- вычисляют значение ср.кв.ош. М арифметической средины.
Что понимают под арифметической срединой? Каким образом её определяют по результатам измерений?
Если в результате равноточных измерений получен ряд измеренных величин l 1 , l 2 , l 3 ... l n , а X - точное значение измеряемой величины, то можно написать ряд случайных ошибок: 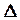 1 = l 1 - X ;
1 = l 1 - X ; 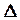 2 = l 2 - X ...
2 = l 2 - X ... 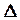 n= = l n - X /
n= = l n - X /
Образовав сумму этих ошибок 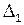 +
+ 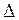 2 +
2 + 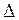 3 + ...+
3 + ...+ 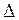 n = l1 + l2 + +l3 +...+ l n , получим [
n = l1 + l2 + +l3 +...+ l n , получим [ 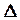 ] = [ l ] - nХ.
] = [ l ] - nХ.
Разделив обе части последнего соотношения на n, имеем
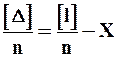 . ( 6 )
. ( 6 )
Согласно свойству случайных ошибок 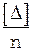 при
при 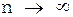 стремится к нулю. Поэтому
стремится к нулю. Поэтому 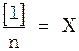 , то-есть
, то-есть 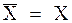 .
.
Следовательно, среднее арифметическое 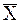 из l измерений выражается формулой
из l измерений выражается формулой
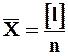 . ( 7 )
. ( 7 )
Кроме того, среднее арифметическое из l измерений стремится к истинному значению измеряемой величины при большом числе измерений n.
E) Погрешности функций измеренных величин
В практике топографо-геодезических работ искомые величины часто определяют как функции измеренных величин. Полученные при этом результаты содержат ошибки, зависящие от вида функции и ошибок аргумента. Рассмотрим основные ошибки функций измеренных величин.
1) Функция вида z = x 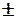 y ( 23 )
y ( 23 )
m 2 z = m 2 x + m2 y ; при m x = m y = m
m z = m 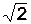 . ( 24 )
. ( 24 )
2) Функция вида z= kx ( 25 )
m z = k m x . ( 26 )
3). Функция вида
z = x 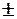 y
y 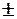 t
t 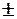 ....
.... 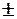 .... u ( 27 )
.... u ( 27 )
m2z = m2 x + m2 y + m2 t +... +... m2 u ; ( 28 )
при m x = m y = mt = ...= m u = m
m z = m 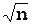 , ( 29 )
, ( 29 )
где n - число аргументов.
4) Функция вида
z = k 1 x1 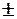 k2 x2
k2 x2 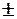 k3 x3
k3 x3 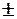 ...
... 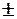 knxn ( 30 )
knxn ( 30 )
m2 z = k21 m 2 x 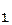 + k22 m2 x
+ k22 m2 x 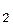 + k23 m 2 x
+ k23 m 2 x 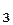 + ....+.... k2 m2 x
+ ....+.... k2 m2 x 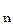 ( 31 )
( 31 )
при к 1 = к 2 = к 3 =...=к n = k
m2 z = k m 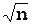 . ( 32 )
. ( 32 )
5). Функция общего вида
z = f ( x 1 , x 2, x 3 .... x n ) ( 33 )
 m 2 z =
m 2 z = 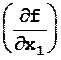
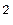 m2
m2 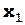 +
+ 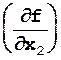
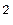 m 2
m 2 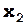 +
+
+ 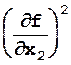 m2
m2 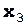 + ...
+ ... 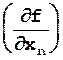 m2
m2 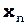 . ( 34 )
. ( 34 )
З) Относительная ошибка
Относительной ошибкой называют отношение абсолютной ошибки измерения к значению измеряемой величины.
Эта ошибка обычно выражается дробью, или в процентах. Она применяется для оценки точности линейных измерений, измерений площадей, объёмов и т.д.
Например, абсолютная ошибка измерения длины линии 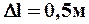 , а длина линии L = 500 м. Относительная ошибка
, а длина линии L = 500 м. Относительная ошибка
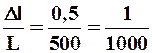 .
. 
 Следует отметить, что точность измерений часто оценивается относительной средней квадратической ошибкой, которая выражается отношением средней квадратической ошибки m измерений к результату измерения L, т.е. m / L .
Следует отметить, что точность измерений часто оценивается относительной средней квадратической ошибкой, которая выражается отношением средней квадратической ошибки m измерений к результату измерения L, т.е. m / L .
Например, линия длиной L = 800 м измерена со ср.кв.ош. m = 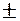 4 см. Относительная средняя квадратическая ошибка в этом случае
4 см. Относительная средняя квадратическая ошибка в этом случае
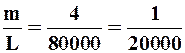 .
.
Арифметического
Оценка точности результатов неравноточных измерений заключается в определении вероятнейшего значения весового арифметического среднего Lо , средней квадратической ошибки отдельного результата измерения 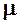 , вес которого равен 1, и средней квадратической ошибки М о арифметической средины.
, вес которого равен 1, и средней квадратической ошибки М о арифметической средины.
При этом значение арифметической средины рассчитывается из соотношения
Lo = 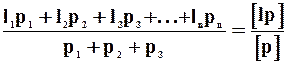 . ( 41 )
. ( 41 )
Вопросы для контроля
1 Классификация измерений и ошибок измерений
2 Свойства случайных ошибок
3 Понятие равноточных измерений. Оценка точности по формуле Гаусса
4 Оценка точности измерений по формуле Бесселя
5 Оценка точности измерений по разностям двойных измерений
6 Понятие относительной ошибки
7 Понятие неравноточных измерений, арифметической средины
8 Оценка точности отдельного результата неравноточного измерения
9 Оценка точности арифметической средины по результатам неравноточных измерений
10 Последовательность оценки точности равноточных измерений
Элементы теории ошибок измерений
Дата: 2018-12-28, просмотров: 645.