Товары не являются заменителями. Напротив, потребители рассматривают товары как дополняющие друг друга в потреблении (например, левый и правый ботинок). В этом случае товары входят в потребительский набор в определенном соотношении. В общем виде функция полезности может быть записана так:

U(x, y) = min{ax, by}.

Коэффициенты а и b показывают соотношение, в котором товары х и у должны входить в потребительский набор. При данных предпочтениях потребитель всегда выбирает набор, в котором ах = bу или x/y = a/b.

Таким образом, допустимые наборы лежат на прямой у = 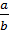·х и нахождение оптимального набора определяется значениями дохода и цен на товары. Если I = Р _x х + Р _y у, то

Графически карта кривых безразличия выглядит так:

Если задано бюджетное ограничение КN, то в качестве оптимального набора потребитель выберет т. С. Как бы не менялись цены товаров и величина дохода, потребитель всегда выберет набор, находящийся на луче OD, где x/y = a/b.

Задача 7

Функция полезности потребителя имеет вид U(x, y) = min{x, 3y}. Цены благ Р_X = 2, Р_Y = 1. Доход потребителя равен 140.

Определите координаты точки равновесия потребителя.

Решение:

Данная функция полезности характеризует такие предпочтения потребителя, при которых товары являются дополняющими друг друга в наборе. В данном примере товары х и у всегда входят в набор в соотношении y/x = 3/1

Следовательно, оптимальный набор может быть найден из условий:

Задача 8

Потребитель тратит имеющиеся у него деньги на покупку двух товаров – х и у. Функция полезности для него имеет вид: U(x, y) = min{4x; 2x + y}. Нарисуйте карту кривых безразличия. Какой выбор сделает потребитель, если Р_X = 3, Р_Y = 1, доход равен 20 ден.ед.?

Решение:

Чтобы представить карту кривых безразличия, запишем функцию полезности следующим образом:

Данные предпочтения графически можно показать следующим образом: область значений у > 2х

Оптимальный набор должен удовлетворять следующим условиям:

Й случай: квазилинейные предпочтения

Квазилинейная функция полезности имеет вид: U(x, y) = y(х) + bу, где y(х) есть возрастающая от х функция (например, y(х) = √x , y(х) = х² и т.п.), b – положительная константа.

Эта функция полезности является линейной относительно у и нелинейной относительно х.

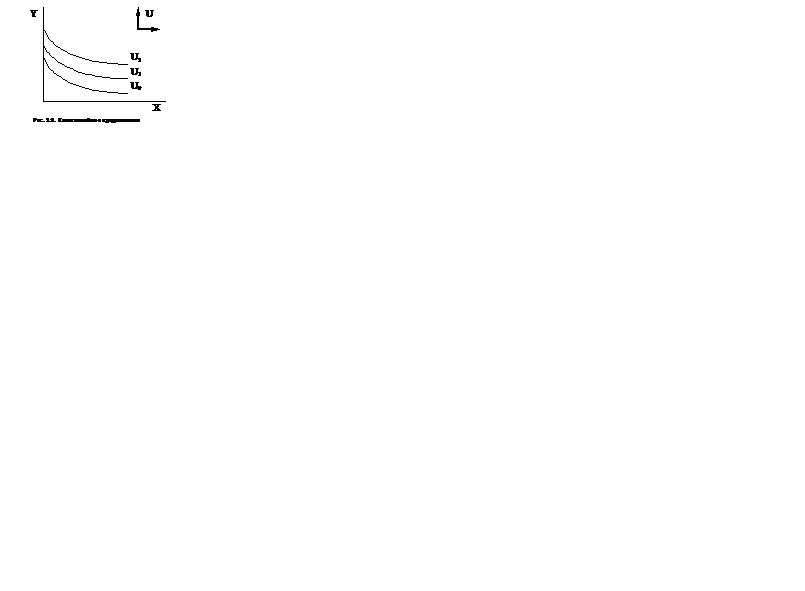
Задача 9

U(x, y) = 2 x + y. Р_X =1, Р_Y = 2, I = 10. Найдите оптимальный выбор потребителя.

Решение:

Найдем предельную норму замещения. Поскольку MU_X = 1/√x, MU_Y = 1, то предельная норма замещения блага у благом х зависит только от количества блага х и не зависит от количества блага у: MRS _XY = MU_X/MU_Y = 1/√x

Если зафиксировать количество блага х в наборе, то MRS_XY будет постоянной величиной, как бы не менялось количество блага у.

Для оптимального выбора должны выполняться условия:

Отсюда получаем х₀ = 4, у₀ = 3. U₀ ( х₀, у₀ ) = 2√4 + 3 = 7.

Итак, при заданных ценах и доходе в оптимальную корзину должно входить не только благо х, но и благо у. Если при тех же ценах на блага будет увеличиваться доход потребителя, то спрос на благо х останется неизменным, а спрос на благо у будет расти.

Задача 10

Потребитель имеет функцию полезности U(x, y) = xy + 10x. Его доход I = 10. Цены благ: Р_X = 1, Р_Y = 2. Найдите оптимальный набор потребителя.

Решение:

Найдем предельную норму замещения функции полезности MRS XY = MU_X/MU_Y = (y+10)/x.

 Для внутреннего оптимума должны выполняться условия:

Данный алгебраический ответ не имеет экономического смысла, поскольку объемы покупаемых благ должны быть неотрицательными. Таким образом, на бюджетном ограничении нет потребительского набора, при котором бюджетная линия является касательной к кривой безразличия. Следовательно, оптимум должен быть в угловой точке. Покажем оптимальный выбор на графике.

Практическое занятие 2