Функций полезности

Случай. Функции полезности – прямые линии (товары – совершенные заменители)

В общем случае такая функция имеет вид U(x, y) = ax + by, где a, b > 0.

Наклон этих прямых постоянен и равен – a / b .

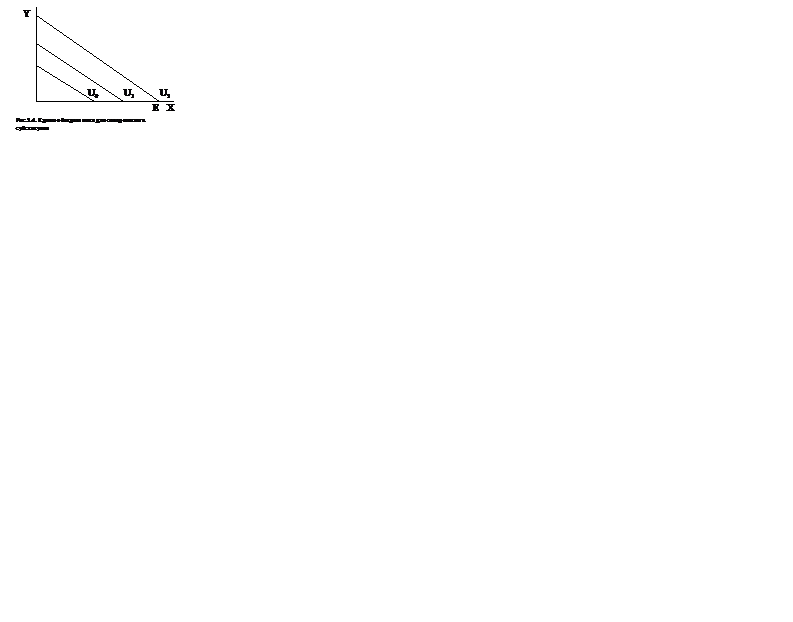
Обратите внимание, что в этом случае линии безразличия пересекают оси координат, следовательно, в оптимальную корзину потребителя может входить не два блага, а только одно. Такое равновесие потребителя называют угловым.

Следует иметь в виду, что кривые безразличия могут пересекать оси координат, но потребитель выбирает внутренний оптимум.

Задача 5

Предпочтения потребителя представлены функцией U = 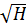 +  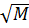, где Н и М – взаимозаменяемые блага. Доход потребителя за неделю составляет 24 ден.ед. Цены заданы как Р _H = 2, Р_M = 1. Сколько блага Н и блага М будет покупать каждую неделю потребитель, если он максимизирует свою полезность?

Решение:

Найдем предельную норму замещения для данной функции полезности

При снижении М и увеличении Н MRS H_M > 0 и является убывающей функцией.

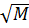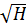Если функцию полезности записать в виде  = U -  (*) или М = ( U - 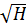)² , то очевидно, что М = 0 (кривая пересекает горизонтальную ось) при Н = U ² . При Н = 0 кривая безразличия пересекает вертикальную ось в т. М = U². Следовательно, можно представить карту кривых безразличий следующим образом (мы учитывали только левую ветку параболы (*), имеющей отрицательный наклон):

В точке оптимума должно выполняться условие касания кривой безразличия и бюджетной линии потребителя, т.е.

Отсюда, М = 4Н. Поскольку 2Н + М = 24, то оптимальный набор благ составляет Н_E = 4; М_E = 16.

Оптимальный уровень полезности U = √4 + √16 = 6.

При данных предпочтениях потребитель всегда выбирает набор, в котором благо М в 4 раза больше, чем благо Н, т.е. допустимые наборы благ лежат на прямой М = 4Н.

Оптимальный выбор определяется как точка пересечения прямой М = 4Н и бюджетной линии 2Н + М = 24, что эквивалентно нахождению точки касания бюджетной линии и кривой безразличия 6 = √H + √M .

Это наивысший уровень полезности, который может быть достигнут при заданных ценах и уровне дохода.

Таким образом, в данном примере кривые безразличия пересекают оси координат, но оптимум является внутренним (Н > 0, М > 0).

Задача 6

Функция полезности потребителя U ( x , y ) = 3 x + y . Пусть Р _X = 2, Р _Y = 1, I = 24. Найдите оптимальный набор для потребителя.

Решение:

Товары х и у являются для потребителя совершенными заменителями, причем

Следовательно, потребитель всегда отказывается от 3 ед. товара y, чтобы увеличить на 1 ед. количество товара х в наборе, не меняя при этом уровень полезности. Таким образом, если отложить товар х по горизонтали, а товар у по вертикали, то наклон любой линии полезности будет равен – 3.

Наклон бюджетной линии равен – P_X / P_Y =-2

Очевидно, в данном случае, чтобы максимизировать полезность, потребитель должен вообще не покупать товар у и все деньги потратить на покупку товара х. В этом случае его оптимальный набор Е(х, у):

у_E = 0; х_E = 24/P_X = 24/2 = 12. Максимальный уровень полезности U(x,y) = 3·12 = 36.