Практическое занятие 2
Теория поведения потребителей
Функция совокупной (общей) полезности:
TU = F(QA,QB,..,QZ),
где ТU – совокупная (общая) полезность данного товарного набора;
QA,QB, …,QZ – объемы потребления товаров А, В, ..., Z в единицу времени.
Существует множество уравнений, описывающих данную функцию, но наиболее часто применяемым является:
TU = а + bq + cq² – dq³,
где q – количество потребленного товара;
a, b, c, d – положительные константы.
Предельная полезность – это прирост совокупной полезности товарного набора при увеличении объема потребления данного товара на одну единицу.
Математически предельная полезность товара есть частная производная совокупной полезности товарного набора по объему потребления i-того товара:
MU=dTU/dQ=TU`(Q),
где MU – предельная полезность товара.
Основное условие потребительского оптимума или Второй закон Госсена: для максимизации полезности потребитель должен таким образом распределить свой ограниченный бюджет, чтобы предельные полезности на один рубль, затраченный на последнюю единицу каждого товара, равнялись бы между собой:
MUА/PА=MUВ/PВ=…=MUZ/PZ,
а сумма всех затрат потребителя на товары и услуги плюс сбережения (S) соответствовала его денежному доходу (R), то есть:
PAQA+PBQB+…+PZQZ+S=R.
Если эти предельные полезности не равны, то совокупное удовлетворение может быть увеличено путем уменьшения расходов на товары с меньшей степенью полезности и увеличения затрат на товары с большей степенью полезности.
Таблица производных простых функций
| 1. Производная константы (числа) |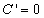 
|
| 2. Производная независимой переменной |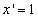 
|
| 3. Производная степени |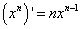 
|
| 4. Производная переменной в степени -1 |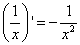 
|
| 5. Производная квадратного корня |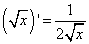 
|
Правила дифференцирования
| 1. Производная суммы или разности |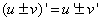 
|
| 2. Производная произведения |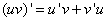 
|
| 2a. Производная выражения, умноженного на постоянный множитель |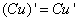 
|
| 3. Производная частного |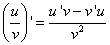 
|
Задача 1.
Индивид потребляет два блага в количествах x и y соответственно. Согласуются ли приведенные ниже функции полезности с аксиомами потребительских предпочтений? (да/нет):
Решение:
Аксиомы потребительских предпочтений:
1) полнота (сопоставимость любых потребительских наборов);
2) транзитивность;
3) ненасыщаемость («больше — лучше, чем меньше», предпочтительность набора, содержащего больший объем любого блага без уменьшения объемов остальных);
4) непрерывность;
5) выпуклость множества наборов, предпочтительных по отношению к любому данному.
Если система предпочтений потребителя задана функцией полезности, то аксиомы 1 и 2 тем самым выполняются. Аксиома 4 выполняется, если функция полезности непрерывна. Во всех вариантах а) – в) функции полезности непрерывны, так что требования аксиом 1, 2 и 4 можно считать выполненными.
Аксиома 3 выполняется, если функция полезности возрастает по каждому аргументу. Функция варианта а), очевидно, удовлетворяет этому требованию, варианта в) — нет, она является убывающей по каждому аргументу. Так как
т. е. значения функций б) и в) — взаимно обратные величины, функция б) является возрастающей (в чем можно убедиться и любым иным способом).
Аксиома 5 требует, чтобы каждая кривая безразличия ограничивала снизу выпуклую область. Это означает, что предельная норма замены MRSxy должна убывать с ростом x и возрастать с ростом y. Функция а) этому требованию не отвечает: соответствующие кривые безразличия – 90-градусные дуги окружностей с центром в начале координат.
Для функции б)
Так что
Таким образом, функция б) удовлетворяет всем аксиомам предпочтений.
Ответ:
а) нет; б) да; в) нет.
Задача 2
Предпочтения индивида характеризуются предельными нормами замещения MRSxy = 2, MRSxz = 0.8. Найти предельные нормы замещения а) MRSyx, б) MRSzx, в) MRSyz, г) MRSzy.
Решение
Если единица блага x замещается a единицами блага y с сохранением уровня полезности, то единица блага y замещается 1/a единицами блага x. Поэтому MRSyx = 1/MRSxy.
Если к тому же единица блага y замещается b единицами блага z при том же условии, то единица блага x замещается ab единицами блага z и поэтому MRSxy ∙ MRSyz = MRSxz.
Это позволяет найти все неизвестные предельные нормы замещения по известным MRSxy и MRSxz.
Комментарий.
Более формализованный подход связывает предельные нормы замены с производными функции полезности:
и т. п., откуда следуют приведенные выше соотношения. Заметим, что система предпочтений определяет функцию полезности неоднозначно: если функция U(x, y, …) описывает предпочтения данного потребителя, то точно так же их описывает функция U 1(x, y, …) = ϕ(U(x, y, …)), где ϕ – произвольная монотонно возрастающая функция. Но
так что отношение частных производных зависит не от количественной шкалы, в которой отображаются полезности, а лишь от предпочтений индивида.
Ответ:
а) 0.5; б) 1.25; в) 0.4; г) 2.5.
Задача 3
Предпочтения потребителя заданы в виде функции полезности U(x, y) = xy. Доход равен 800 ден.ед. Цены благ соответственно равны РX = 20, РY = 40. Чему будет равен набор для потребителя?
Решение:
Запишем задачу в общем виде:
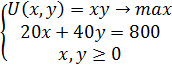
Поскольку оптимум в этом примере является внутренним, то должно выполняться условие MRS XY = MUx / MUy = Px / Py или y / x = 20/40, т.е. х = 2у.
Таким образом, оптимальный набор должен находиться на прямой х = 2у и в то же время удовлетворять бюджетному ограничению. Получаем систему из 2-х линейных уравнений:
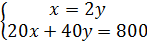
Ее решение дает оптимальный набор у E = 10; х E = 20. Графическая интерпретация этой задачи:
Задача 4
Домашнее хозяйство потребляет два блага в количествах x и y; его предпочтения описываются функцией полезности U(x, y). Найти расходы потребителя на 1 и 2 блага, если а) U(x, y) = x3y2; б) U(x, y) = xαyβ.
Решение:
а) Прежде всего, определим предельную норму замены как функцию x и y: Ux = 3x2y2; Uy = 2x3y, отсюда
При ценах благ px, py в точке оптимума потребителя соотношение цен px/py равно предельной норме замены, так что
Или
Заметим, что pxx и pyy – это расходы потребителя соответственно на первое и второе блага. Отсюда ясно, как данный потребитель распределяет свой бюджет: долю 0.6 своего дохода он должен потратить на покупку первого блага, долю 0.4 – на покупку второго. Если его доход равен I, то объемы спроса на первое и на второе благо равны:
Каждое из приведенных равенств описывает функцию спроса на соответствующее благо.
б) Те же рассуждения применительно к более общему случаю приводят к соотношению:
Откуда
Функций полезности
Задача 5
Предпочтения потребителя представлены функцией U =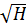 
+ 
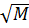, где Н и М – взаимозаменяемые блага. Доход потребителя за неделю составляет 24 ден.ед. Цены заданы как Р H = 2, РM = 1. Сколько блага Н и блага М будет покупать каждую неделю потребитель, если он максимизирует свою полезность?
Решение:
Найдем предельную норму замещения для данной функции полезности
При снижении М и увеличении Н MRS HM > 0 и является убывающей функцией.
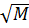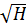Если функцию полезности записать в виде = U - (*) или М = ( U - 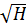)2 , то очевидно, что М = 0 (кривая пересекает горизонтальную ось) при Н = U 2 . При Н = 0 кривая безразличия пересекает вертикальную ось в т. М = U2. Следовательно, можно представить карту кривых безразличий следующим образом (мы учитывали только левую ветку параболы (*), имеющей отрицательный наклон):
В точке оптимума должно выполняться условие касания кривой безразличия и бюджетной линии потребителя, т.е.
Отсюда, М = 4Н. Поскольку 2Н + М = 24, то оптимальный набор благ составляет НE = 4; МE = 16.
Оптимальный уровень полезности U = √4 + √16 = 6.
При данных предпочтениях потребитель всегда выбирает набор, в котором благо М в 4 раза больше, чем благо Н, т.е. допустимые наборы благ лежат на прямой М = 4Н.
Оптимальный выбор определяется как точка пересечения прямой М = 4Н и бюджетной линии 2Н + М = 24, что эквивалентно нахождению точки касания бюджетной линии и кривой безразличия 6 = √H + √M .
Это наивысший уровень полезности, который может быть достигнут при заданных ценах и уровне дохода.
Таким образом, в данном примере кривые безразличия пересекают оси координат, но оптимум является внутренним (Н > 0, М > 0).
Задача 6
Функция полезности потребителя U ( x , y ) = 3 x + y . Пусть Р X = 2, Р Y = 1, I = 24. Найдите оптимальный набор для потребителя.
Решение:
Товары х и у являются для потребителя совершенными заменителями, причем
Следовательно, потребитель всегда отказывается от 3 ед. товара y, чтобы увеличить на 1 ед. количество товара х в наборе, не меняя при этом уровень полезности. Таким образом, если отложить товар х по горизонтали, а товар у по вертикали, то наклон любой линии полезности будет равен – 3.
Наклон бюджетной линии равен – PX / PY =-2
Очевидно, в данном случае, чтобы максимизировать полезность, потребитель должен вообще не покупать товар у и все деньги потратить на покупку товара х. В этом случае его оптимальный набор Е(х, у):
уE = 0; хE = 24/PX = 24/2 = 12. Максимальный уровень полезности U(x,y) = 3·12 = 36.
Задача 7
Функция полезности потребителя имеет вид U(x, y) = min{x, 3y}. Цены благ РX = 2, РY = 1. Доход потребителя равен 140.
Определите координаты точки равновесия потребителя.
Решение:
Данная функция полезности характеризует такие предпочтения потребителя, при которых товары являются дополняющими друг друга в наборе. В данном примере товары х и у всегда входят в набор в соотношении y/x = 3/1
Следовательно, оптимальный набор может быть найден из условий:
Задача 8
Потребитель тратит имеющиеся у него деньги на покупку двух товаров – х и у. Функция полезности для него имеет вид: U(x, y) = min{4x; 2x + y}. Нарисуйте карту кривых безразличия. Какой выбор сделает потребитель, если РX = 3, РY = 1, доход равен 20 ден.ед.?
Решение:
Чтобы представить карту кривых безразличия, запишем функцию полезности следующим образом:
Данные предпочтения графически можно показать следующим образом: область значений у > 2х
Оптимальный набор должен удовлетворять следующим условиям:
Задача 9
U(x, y) = 2 x + y. РX =1, РY = 2, I = 10. Найдите оптимальный выбор потребителя.
Решение:
Найдем предельную норму замещения. Поскольку MUX = 1/√x, MUY = 1, то предельная норма замещения блага у благом х зависит только от количества блага х и не зависит от количества блага у: MRS XY = MUX/MUY = 1/√x
Если зафиксировать количество блага х в наборе, то MRSXY будет постоянной величиной, как бы не менялось количество блага у.
Для оптимального выбора должны выполняться условия:
Отсюда получаем х0 = 4, у0 = 3. U0 ( х0, у0 ) = 2√4 + 3 = 7.
Итак, при заданных ценах и доходе в оптимальную корзину должно входить не только благо х, но и благо у. Если при тех же ценах на блага будет увеличиваться доход потребителя, то спрос на благо х останется неизменным, а спрос на благо у будет расти.
Задача 10
Потребитель имеет функцию полезности U(x, y) = xy + 10x. Его доход I = 10. Цены благ: РX = 1, РY = 2. Найдите оптимальный набор потребителя.
Решение:
Найдем предельную норму замещения функции полезности MRS XY = MUX/MUY = (y+10)/x.
Для внутреннего оптимума должны выполняться условия:
Данный алгебраический ответ не имеет экономического смысла, поскольку объемы покупаемых благ должны быть неотрицательными. Таким образом, на бюджетном ограничении нет потребительского набора, при котором бюджетная линия является касательной к кривой безразличия. Следовательно, оптимум должен быть в угловой точке. Покажем оптимальный выбор на графике.
Практическое занятие 2
Таблица производных простых функций
| 1. Производная константы (числа) |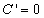
|
| 2. Производная независимой переменной |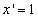
|
| 3. Производная степени |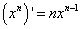
|
| 4. Производная переменной в степени -1 |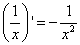
|
| 5. Производная квадратного корня |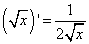
|
Правила дифференцирования
| 1. Производная суммы или разности |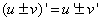
|
| 2. Производная произведения |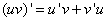
|
| 2a. Производная выражения, умноженного на постоянный множитель |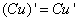
|
| 3. Производная частного |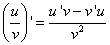
|
Задача 1.
Индивид потребляет два блага в количествах x и y соответственно. Согласуются ли приведенные ниже функции полезности с аксиомами потребительских предпочтений? (да/нет):
Задача 2
Предпочтения индивида характеризуются предельными нормами замещения MRSxy = 2, MRSxz = 0.8. Найти предельные нормы замещения а) MRSyx, б) MRSzx, в) MRSyz, г) MRSzy.
Задача 3
Предпочтения потребителя заданы в виде функции полезности U(x, y) = xy. Доход равен 800 ден.ед. Цены благ соответственно равны РX = 20, РY = 40. Чему будет равен набор для потребителя?
Задача 4
Домашнее хозяйство потребляет два блага в количествах x и y; его предпочтения описываются функцией полезности U(x, y). Найти расходы потребителя на 1 и 2 блага, если а) U(x, y) = x3y2; б) U(x, y) = xαyβ.
Функций полезности
Задача 5
Предпочтения потребителя представлены функцией U = 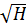+ 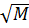, где Н и М – взаимозаменяемые блага. Доход потребителя за неделю составляет 24 ден.ед. Цены заданы как Р H = 2, РM = 1. Сколько блага Н и блага М будет покупать каждую неделю потребитель, если он максимизирует свою полезность?
Задача 6
Функция полезности потребителя U ( x , y ) = 3 x + y . Пусть Р X = 2, Р Y = 1, I = 24. Найдите оптимальный набор для потребителя.
Задача 7
Функция полезности потребителя имеет вид U(x, y) = min{x, 3y}. Цены благ РX = 2, РY = 1. Доход потребителя равен 140.
Определите координаты точки равновесия потребителя.
Задача 8
Потребитель тратит имеющиеся у него деньги на покупку двух товаров – х и у. Функция полезности для него имеет вид: U(x, y) = min{4x; 2x + y}. Нарисуйте карту кривых безразличия. Какой выбор сделает потребитель, если РX = 3, РY = 1, доход равен 20 ден.ед.?
Задача 9
U(x, y) = 2 x + y. РX =1, РY = 2, I = 10. Найдите оптимальный выбор потребителя.
Задача 10
Потребитель имеет функцию полезности U(x, y) = xy + 10x. Его доход I = 10. Цены благ: РX = 1, РY = 2. Найдите оптимальный набор потребителя.
Практическое занятие 2
Теория поведения потребителей
Функция совокупной (общей) полезности:
TU = F(QA,QB,..,QZ),
где ТU – совокупная (общая) полезность данного товарного набора;
QA,QB, …,QZ – объемы потребления товаров А, В, ..., Z в единицу времени.
Существует множество уравнений, описывающих данную функцию, но наиболее часто применяемым является:
TU = а + bq + cq² – dq³,
где q – количество потребленного товара;
a, b, c, d – положительные константы.
Предельная полезность – это прирост совокупной полезности товарного набора при увеличении объема потребления данного товара на одну единицу.
Математически предельная полезность товара есть частная производная совокупной полезности товарного набора по объему потребления i-того товара:
MU=dTU/dQ=TU`(Q),
где MU – предельная полезность товара.
Основное условие потребительского оптимума или Второй закон Госсена: для максимизации полезности потребитель должен таким образом распределить свой ограниченный бюджет, чтобы предельные полезности на один рубль, затраченный на последнюю единицу каждого товара, равнялись бы между собой:
MUА/PА=MUВ/PВ=…=MUZ/PZ,
а сумма всех затрат потребителя на товары и услуги плюс сбережения (S) соответствовала его денежному доходу (R), то есть:
PAQA+PBQB+…+PZQZ+S=R.
Если эти предельные полезности не равны, то совокупное удовлетворение может быть увеличено путем уменьшения расходов на товары с меньшей степенью полезности и увеличения затрат на товары с большей степенью полезности.
Таблица производных простых функций
| 1. Производная константы (числа) |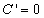
|
| 2. Производная независимой переменной |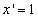
|
| 3. Производная степени |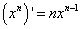
|
| 4. Производная переменной в степени -1 |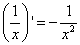
|
| 5. Производная квадратного корня |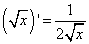
|
Правила дифференцирования
| 1. Производная суммы или разности |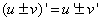
|
| 2. Производная произведения |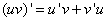
|
| 2a. Производная выражения, умноженного на постоянный множитель |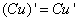
|
| 3. Производная частного |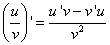
|
Задача 1.
Индивид потребляет два блага в количествах x и y соответственно. Согласуются ли приведенные ниже функции полезности с аксиомами потребительских предпочтений? (да/нет):
Решение:
Аксиомы потребительских предпочтений:
1) полнота (сопоставимость любых потребительских наборов);
2) транзитивность;
3) ненасыщаемость («больше — лучше, чем меньше», предпочтительность набора, содержащего больший объем любого блага без уменьшения объемов остальных);
4) непрерывность;
5) выпуклость множества наборов, предпочтительных по отношению к любому данному.
Если система предпочтений потребителя задана функцией полезности, то аксиомы 1 и 2 тем самым выполняются. Аксиома 4 выполняется, если функция полезности непрерывна. Во всех вариантах а) – в) функции полезности непрерывны, так что требования аксиом 1, 2 и 4 можно считать выполненными.
Аксиома 3 выполняется, если функция полезности возрастает по каждому аргументу. Функция варианта а), очевидно, удовлетворяет этому требованию, варианта в) — нет, она является убывающей по каждому аргументу. Так как
т. е. значения функций б) и в) — взаимно обратные величины, функция б) является возрастающей (в чем можно убедиться и любым иным способом).
Аксиома 5 требует, чтобы каждая кривая безразличия ограничивала снизу выпуклую область. Это означает, что предельная норма замены MRSxy должна убывать с ростом x и возрастать с ростом y. Функция а) этому требованию не отвечает: соответствующие кривые безразличия – 90-градусные дуги окружностей с центром в начале координат.
Для функции б)
Так что
Таким образом, функция б) удовлетворяет всем аксиомам предпочтений.
Ответ:
а) нет; б) да; в) нет.
Задача 2
Предпочтения индивида характеризуются предельными нормами замещения MRSxy = 2, MRSxz = 0.8. Найти предельные нормы замещения а) MRSyx, б) MRSzx, в) MRSyz, г) MRSzy.
Решение
Если единица блага x замещается a единицами блага y с сохранением уровня полезности, то единица блага y замещается 1/a единицами блага x. Поэтому MRSyx = 1/MRSxy.
Если к тому же единица блага y замещается b единицами блага z при том же условии, то единица блага x замещается ab единицами блага z и поэтому MRSxy ∙ MRSyz = MRSxz.
Это позволяет найти все неизвестные предельные нормы замещения по известным MRSxy и MRSxz.
Комментарий.
Более формализованный подход связывает предельные нормы замены с производными функции полезности:
и т. п., откуда следуют приведенные выше соотношения. Заметим, что система предпочтений определяет функцию полезности неоднозначно: если функция U(x, y, …) описывает предпочтения данного потребителя, то точно так же их описывает функция U 1(x, y, …) = ϕ(U(x, y, …)), где ϕ – произвольная монотонно возрастающая функция. Но
так что отношение частных производных зависит не от количественной шкалы, в которой отображаются полезности, а лишь от предпочтений индивида.
Ответ:
а) 0.5; б) 1.25; в) 0.4; г) 2.5.
Задача 3
Предпочтения потребителя заданы в виде функции полезности U(x, y) = xy. Доход равен 800 ден.ед. Цены благ соответственно равны РX = 20, РY = 40. Чему будет равен набор для потребителя?
Решение:
Запишем задачу в общем виде:
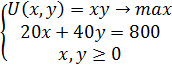
Поскольку оптимум в этом примере является внутренним, то должно выполняться условие MRS XY = MUx / MUy = Px / Py или y / x = 20/40, т.е. х = 2у.
Таким образом, оптимальный набор должен находиться на прямой х = 2у и в то же время удовлетворять бюджетному ограничению. Получаем систему из 2-х линейных уравнений:
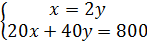
Ее решение дает оптимальный набор у E = 10; х E = 20. Графическая интерпретация этой задачи:
Задача 4
Домашнее хозяйство потребляет два блага в количествах x и y; его предпочтения описываются функцией полезности U(x, y). Найти расходы потребителя на 1 и 2 блага, если а) U(x, y) = x3y2; б) U(x, y) = xαyβ.
Решение:
а) Прежде всего, определим предельную норму замены как функцию x и y: Ux = 3x2y2; Uy = 2x3y, отсюда
При ценах благ px, py в точке оптимума потребителя соотношение цен px/py равно предельной норме замены, так что
Или
Заметим, что pxx и pyy – это расходы потребителя соответственно на первое и второе блага. Отсюда ясно, как данный потребитель распределяет свой бюджет: долю 0.6 своего дохода он должен потратить на покупку первого блага, долю 0.4 – на покупку второго. Если его доход равен I, то объемы спроса на первое и на второе благо равны:
Каждое из приведенных равенств описывает функцию спроса на соответствующее благо.
б) Те же рассуждения применительно к более общему случаю приводят к соотношению:
Откуда
Дата: 2018-12-28, просмотров: 1507.
