Задача 1
Две звезды массы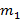 
и 
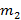образуют двойную звезду с постоянным расстоянием R между звездами. Каков период обращения данной двойной звезды?
Ответ: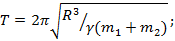 
Задача 2
Три звезды массы m каждая образуют равносторонний треугольник со стороной L. С какой угловой скоростью вращается этот треугольник?
Ответ: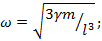 
Задача 3
Спутник движется со скоростью v по круговой орбите вокруг Земли. Какую наименьшую добавочную скорость надо сообщить спутнику, чтобы он мог безвозвратно уйти от Земли?
Ответ: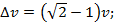 
Задача 4
Скорость пылинок однородного шарового облака направлена радиально наружу и в начальный момент пропорциональна расстоянию до центра облака. При какой наибольшей начальной плотности облако будет неограниченно расширяться?
Ответ: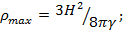 
Задача 5
Спутник связи имеет перигей над южным полушарием Земли на высоте около 500 км, а апогей на высоте около 40000 км над северным полушарием. Каково отношение угловых скоростей обращения этого спутника в перигее и апогее?
Ответ: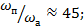 
Задача 6
Скорость спутника в перигее равна v при расстоянии до центра Земли, равном r. Какова скорость спутника в апогее? Каково расстояние от него до центра земли в апогее?
Ответ: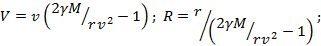 
Задача 7
Определите силу натяжения троса, связывающего два спутника массы m, которые обращаются вокруг Земли на расстояниях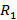 
и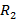 
от ее центра так, что трос всегда направлен радиально. Масса Земли M.
Ответ: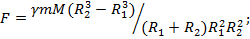 
Статика
Задача 1
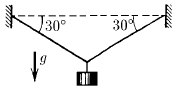
Между двумя стенками на нерастяжимом невесомом тросе висит груз массы m, найдите силу натяжения троса.
Ответ
Задача 2
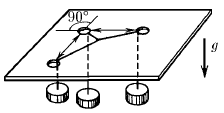
Через три отверстия в крышке стола пропущены нити, связанные с одного конца общим узлом. К другому концу каждой нити прикреплены одинаковые грузы. Найдите углы между нитями. Трением пренебречь.
Ответ: 120°
Задача 3
На сколько сместится конец нити, перекинутой через подвижный блок, если к нему приложить силу F? Жесткость пружин равна k.
Ответ: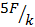 
Задача 4
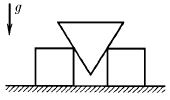
Между одинаковыми брусками квадратного сечения, лежащими на горизонтальной плоскости, вставлен гладкий клин такой же массы с сечением в виде равностороннего треугольника. При каком коэффициенте трения брусков о плоскость они начнут разъезжаться?
Ответ: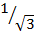 
Задача 5
Неравноплечие весы находятся в равновесии. Если на левую их чашку положить груз, то он уравновешивается гирей массы 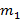на правой чашке. Если этот же груз положить на правую чашку, то он уравновешивается грузом массы 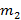на левой чашке. Какова масса груза?
Ответ: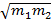 
Задача 6
С какой силой давит на стенки цилиндрического стакана палочка массы m, наполовину погруженная в воду? Угол наклона палочки к горизонтали α. Трением пренебречь.
Ответ: 
Задача 7
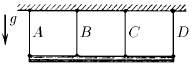Однородная балка длины l висит на четырех одинаковых тросах, прикрепленных на расстоянии l /3 друг от друга. Трос A порвался. Для уменьшения опасности разрыва других тросов предлагают удалить еще и канат D. Разумно ли это решение?
Ответ: Разумно
Задача 8
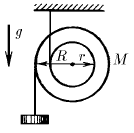
Катушка висит на нити, намотанной по малому радиусу r катушки. По большому радиусу R тоже намотана нить, на конце которой висит груз. Какова масса груза, если система находится в равновесии? Масса катушки M.
Ответ: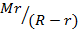 
Механика жидкости. (… занятий)
Давление жидкости.
Задача 1
Результирующая сила, действующая со стороны сжатой жидкости на три грани правильного тетраэдра, равна F. Длина ребра тетраэдра a. Определите давление жидкости.
Ответ: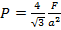 
Задача 2
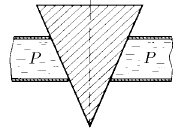
Коническая пробка перекрывает сразу два отверстия в плоском сосуде, заполненном жидкостью при давлении P. Радиус отверстий r и R. Определите силу, действующую на пробку со стороны жидкости.
Ответ: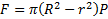 
;
Задача 3
Сферический баллон радиуса R со стенками толщины Δ разрывается внутренним давлением P. Определите предел прочности материала стенок.
Ответ: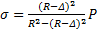 
;
Задача 4
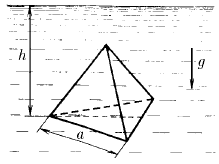
Нижняя грань правильного тетраэдра с ребром a, полностью погруженного в жидкость плотности ρ, находится на глубине h. Определите силу, действующую со стороны жидкости на боковую грань тетраэдра, если атмосферное давление равно P.
Ответ: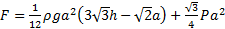 
;
Задача 5
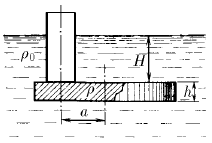
Трубка радиуса r закрыта снизу металлическим диском и погружена в жидкость на глубину H. Радиус диска R, высота h. Ось диска отстоит от оси трубки на расстояние a. Плотность жидкости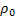 
, плотность металла ρ. До какой высоты нужно наливать жидкость в трубку, чтобы диск оторвался от трубки?
Ответ: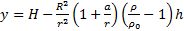 
;
Задача 6
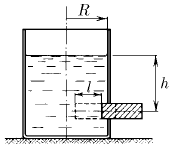
В цилиндрическом сосуде радиуса R, частично наполненном жидкостью плотности ρ, в боковой стенке имеется отверстие, заткнутое пробкой. Какую работу нужно совершить, чтобы вдвинуть пробку на длину l? Пробка имеет вид цилиндра радиуса r. Центр отверстия находится на глубине h. Сосуд достаточно высок, чтобы жидкость из него не выливалась. Трение не учитывать.
Ответ: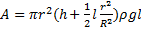 
;
Задача 7
Под каким углом к горизонту расположится поверхность жидкости в сосуде, скользящем по наклонной плоскости, составляющей угол α с горизонтом, если коэффициент трения равен µ?
Ответ: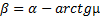 
Задача 8
Закрытый цилиндр радиуса R, заполненный на три четверти своего объема жидкостью плотности ρ, вращается в невесомости вместе с жидкостью с угловой скоростью ω вокруг своей оси. Как меняется давление в жидкости в зависимости от расстояния до стенок цилиндра?
Ответ: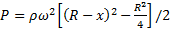 
.
3.2. Плавание тел. Закон Архимеда.
Задача 1
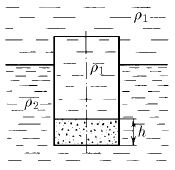
Тонкостенный цилиндрический стакан массы m вертикально плавает на границе раздела жидкостей плотност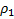и 
и 
. Определите глубину погружения стакана в нижнюю жидкость, если дно стакана имеет толщину h и площадь S, а сам стакан заполнен жидкостью плотности .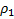
Ответ: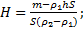 
Задача 2
В жидкости плотности 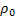плавает прямоугольный параллелепипед из материала плотности ρ. Высота параллелепипеда b, а ширина и длина a. При каком соотношении a и b его положение устойчиво?
Ответ: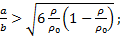 
Задача 3
С какой силой давит тяжелая палочка на дно водоема, если жестко связанный с палочкой пустотелый шарик радиуса r погрузился в жидкость наполовину? Плотность жидкости ρ, длина палочки l.
Ответ: 
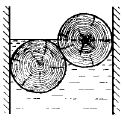
Задача 4
Определите силу давления бревен массы m на стенки канала. Верхнее бревно погружено в воду наполовину, а нижнее касается верхним участком поверхности воды. Бревна одинаковы.
Ответ: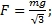 
Задача 5
Коническая пробка с радиусом основания R закрывает сливное отверстие радиуса r ванны. Какой должна быть масса пробки, чтобы она не всплывала при наполнении ванны жидкостью плотности ρ.
Ответ: 
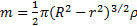
Задача 6
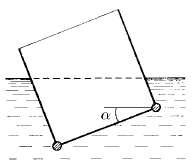
Наклон кубической коробки, наполовину погруженной в жидкость, равен α. Определите массу каждого из двух противоположных ребер коробки. Массой остальных частей коробки пренебречь. Плотность жидкости ρ, длина ребер a.
Ответ: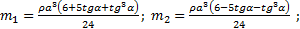 
Задача 7
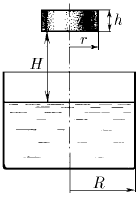
В цилиндр радиуса R, частично заполненный жидкостью падает цилиндрическая пробка радиуса r и высоты h. Начальная высота нижней поверхности над уровнем жидкости H, начальная скорость равна нулю. Какое количество теплоты выделится к моменту окончания движения жидкости и пробки? Плотность пробки ρ, плотность жидкости 
.
Ответ: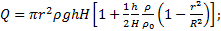 
Задача 8
Цилиндрический сосуд радиуса R, частично заполненный жидкостью вращается вместе с жидкостью вокруг своей оси. К боковой стенке сосуда на нити длины l привязан воздушный шарик радиуса r. Во время вращения нить образует со стенкой угол α. Определите угловую скорость вращения сосуда.
Ответ: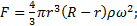 
Течение идеальной жидкости.
Задача 1
Сосуд с водой подвешен к потолку. Высота воды в сосуде h. На сколько изменится сила натяжения подвеса, если в дне сосуда открыть маленькое отверстие из которого будет вытекать струя сечения S? Плотность воды ρ.
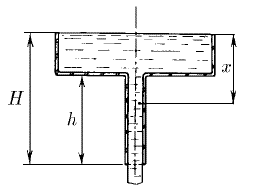Ответ: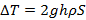 
Задача 2
Из широкого сосуда через узкую цилиндрическую трубку в его дне вытекает жидкость плотности ρ. Как распределены по вертикали давление и скорость жидкости в сосуде и трубке? Давление воздуха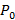 
.
Ответ: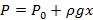 
в сосуде и 
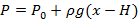в трубке
Задача 3
По длинной наклонной плоскости стекает широкий поток воды. На протяжении l по течению глубина потока уменьшается вдвое. На протяжении какого пути глубина потока уменьшится в четыре раза?
Ответ: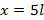 
Задача 4
По изогнутой под прямым углом трубе поперечного сечения S со скоростью v течет жидкость плотности ρ. С какой силой жидкость действует на трубу, если давление на выходе из трубы P? Силой тяжести пренебречь.
Ответ: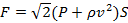 
Задача 5
Широкая струя жидкости толщины h падает под углом α на плоскость. На струи какой толщины распадается падающая струя?
Ответ: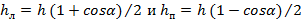 
Задача 6
В цилиндре с поршнем находится вода, внутри которой в начальный момент имеется полость объема V. Поршень оказывает на воду постоянное давление P. Какую энергию приобретает вода в момент, когда полость исчезнет?
Ответ: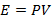 
Течение вязкой жидкости.
Задача 1
Найдите распределение скорости жидкости при установившемся ее течении между двумя плоскостями. Расстояние между плоскостями h, вязкость жидкости η. Найдите расход жидкости на единицу ширины потока, если перепад давления на единицу длины потока равен P.
Ответ: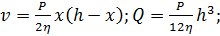 
Задача 2
Жидкость перекачивается из одного сосуда в другой через длинную трубку радиуса R и длины l. Разность давлений на концах трубки P, вязкость жидкости η. Определите зависимость градиента скорости жидкости от расстояния до стенки трубки.
Ответ: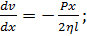 
Задача 3
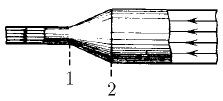В трубе переменного сечения поддерживается стационарное течение вязкой жидкости. В сечениях 1 и 2 скорость можно считать постоянной по сечению. Площади сечений 1 и 2 равны 
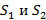, а давление жидкости соответственно 
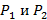. Скорость жидкости в сечении 1 равна 
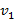. Найдите силу, с которой жидкость действует на участок трубы между сечениями 1 и 2.
Ответ: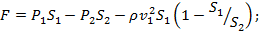 
Дата: 2018-12-28, просмотров: 384.
