Занятие 2
Задача 8
Нарисуйте график зависимости координаты от времени для прямолинейного движения, удовлетворяющего одновременно двум условиям: средняя скорость в промежутке от 2 до 6 с равна 5 м/с, максимальная скорость в том же промежутке равна 15 м/с.
Задача 9
Частица, покинув источник, пролетает с постоянной скоростью расстояние L, а затем тормозится с ускорением a. При какой начальной скорости время движения от ее вылета до остановки будет наименьшим?
Задача 10
В коническом сосуде уровень воды поднимается с постоянной скоростью v 0. Как зависит от времени скорость поступления воды в сосуд через трубку сечения s? В нулевой момент времени сосуд пуст.
Задача 11
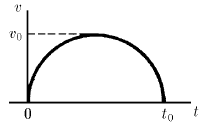
График зависимости скорости тела от времени имеет вид полуокружности. Максимальная скорость тела равна v 0, время движения t 0. Определите путь, пройденный телом.
Задача 12
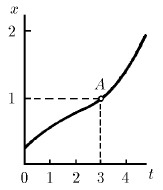
Графики зависимости координаты от времени, построенные в различном масштабе времени для двух частиц, оказались одинаковыми. Одно деление оси времени t для графика первой частицы отвечает 4 с, а для графика второй – 1 с. Найдите отношение скоростей и отношение ускорений частиц для точки А графика.
Задача 13
Тело начинает движение из точки А и движется сначала равноускоренно в течение времени t 0, а затем равнозамедленно, с тем же по модулю ускорением. Через какое время от начала движения тело вернется в точку А?
Задача 14
Из одной и той же точки вертикально вверх с интервалом времени ∆ t брошены два шарика со скоростью v. Через какое время после вылета второго шарика они столкнутся?
Движение в поле тяжести. Криволинейное движение.
Занятие 3
Задача 15
Из верхней точки окружности по гладкому желобу под углом φ к вертикали начинает скользить шарик. За какое время он достигнет окружности, если ее диаметр равен D?
Задача 16
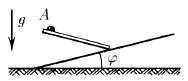Под каким углом к вертикали должен быть направлен из точки А гладкий желоб, чтобы шарик соскользнул по нему на наклонную плоскость за наименьшее время?
Задача 17
Из орудия произведен выстрел под углом φ к горизонту. Начальная скорость снаряда v. Поверхность земли горизонтальна. Найдите: горизонтальную и вертикальную компоненты скорости как функцию от времени; зависимость координат х и у от времени; уравнение траектории, т.е. зависимость у от х; время полета, наибольшую высоту и дальность полета снаряда.
Задача 18
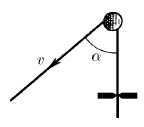
С какой скоростью должен в момент старта ракеты вылететь из пушки снаряд, чтобы поразить стартующую вертикально, с ускорением а, ракету? Расстояние от пушки до стартового стола L, пушка стреляет под углом α к горизонту.
Задача 19
Из шланга лежащего на земле под углом α к горизонту бьет струя воды со скоростью v. Определите массу струи находящейся в воздухе, если площадь ее сечения неизменна и равна s.
Занятие 4
Задача 20
Снаряд, вылетев из орудия со скоростью v попал в точку с координатами х и у. Найдите: тангенс угла наклона, образуемого стволом орудия и горизонтом; границу области возможного попадания снаряда; наименьшую потребную скорость снаряда, при которой он сможет поразить цель с координатами [х,у].
Задача 21
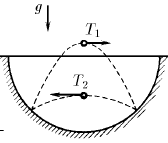
В сферической лунке прыгает шарик упруго ударяясь о ее стенки в двух точках, расположенных на одной горизонтали. Промежуток времени между ударами при движении шарика слева направо равен Т1, а справа налево Т2. Определите радиус лунки.
Задача 22
Определите скорость и ускорение, которыми обладают точки земной поверхности на экваторе и в Санкт-Петербурге из-за вращения Земли вокруг своей оси. Радиус Земли принять равным 6400 км. Санкт-Петербург находится на 60° с.ш.
Задача 23
Край гладкого горизонтального стола скруглен по окружности радиуса r. С какой наименьшей скоростью нужно пустить по столу маленькое тело, чтобы оно, достигнув начала скругления, сразу полетело по параболе?
1.4. Преобразование Галилея.
Занятие 5
Задача 24
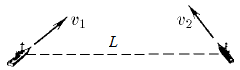Начальные положения и скорости двух кораблей заданы на рисунке. Корабли движутся без ускорения. Найдите наименьшее расстояние между ними.
Задача 25
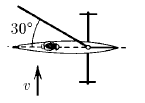Буер представляет собой сани с парусом, и может двигаться лишь по прямой, вдоль которой направлены его коньки. Ветер дует со скоростью v перпендикулярно направлению движения буера. Парус отклонен на 30° относительно направления движения буера. Какую максимальную скорость может развить буер в таких условиях?
Задача 26
При упругом ударе тела о неподвижную стенку его скорость v меняется лишь по направлению. Определите изменение скорости после удара этого тела, если стенка движется: со скоростью u навстречу телу; со скоростью w < v в направлении движения тела.
Задача 27
Ядро, летящее со скоростью v, распадается на два одинаковых осколка. Определите максимальный возможный угол α между скоростями одного из осколков и вектором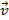 
, если при распаде покоящегося ядра осколки имеют скорость u < v.
Задача 28
Мальчик может плавать со скоростью в два раза меньшей скорости течения реки. Он хочет переплыть реку так, чтобы его как можно меньше снесло вниз по течению. Под каким углом к берегу он должен плыть? На какое расстояние его снесет, если ширина реки равна 200 м?
Движение со связями.
Занятие 6
Задача 29
Четыре черепахи находятся в вершинах квадрата со стороной а. Они начинают двигаться одновременно с постоянной по модулю скоростью v. Каждая черепаха движется по направлению к своей соседке по часовой. Где и через какое время встретятся черепахи?
Задача 30
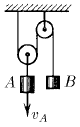
На рисунке скорость груза А равна v A. Чему равна скорость груза В?
Задача 31
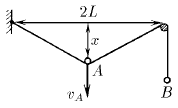Постройте примерный график зависимости скорости точки В от времени если скорость v A точки А постоянна. Найдите формулу этой зависимости при x (0) = 0 и постройте ее график.
Задача 32
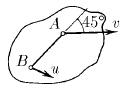Скорость точки А твердого тела равна v и образует угол 45° с направлением прямой AB. Скорость точки В этого тела равна u. Определите проекцию скорости точки B на направление АВ.
Задача 33
Найдите зависимость скорости точки поверхности колеса радиуса R от ее положения на поверхности (угла α между вертикалью, проходящей через ось колеса, и направлением на точку) и скорости колеса V. Проскальзывания между колесом и горизонтальной подстилающей поверхностью нет.
Задача 34
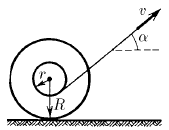Нить, намотанную на ось катушки, тянут со скоростью v под углом α к горизонту. Катушка катится по горизонтальной плоскости без проскальзывания. Найдите скорость оси и угловую скорость вращения катушки. При каких углах α ось движется вправо, а при каких влево? Нить достаточно длинна и не провисает, таким образом угол α остается постоянным.
Задача 35
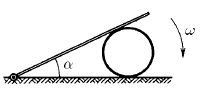Стержень, шарнирно закрепленный одним концом на горизонтальной плоскости, лежит на цилиндре. Угловая скорость стержня равна ω. Проскальзывания между цилиндром и плоскостью нет. Найдите зависимость угловой скорости цилиндра от угла α между стержнем и плоскостью.
Динамика.
Законы Ньютона.
Занятие 1
Задача 1
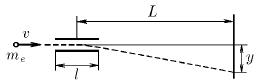В электронно-лучевой трубке электроны с начальной горизонтальной скоростью v влетают в область электрического поля протяженности l, где на них действует вертикальная сила со стороны заряженных отклоняющих пластин. Чему равна эта сила, если электроны, попадая на экран, смещаются на расстояние y по сравнению со случаем незаряженных пластин? Экран находится на расстоянии L от центра области действия электрической силы. Масса электрона me.
Задача 2
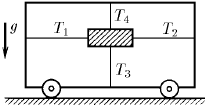Четырьмя натянутыми нитями груз закреплен на тележке. Сила натяжения горизонтальных нитей соответственно T 1 и T 2, а вертикальных – T 3 и T 4. С каким ускорением движется тележка по горизонтальной плоскости?
Задача 3
Динамометр состоит из двух цилиндров, соединенных легкой пружиной. Найдите соотношение масс этих цилиндров, если при приложенных к ним силам F 1 и F 2 динамометр показывает силу F.
Задача 4
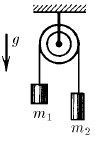
Два груза массой соответственно m 1 и m 2 соединены нитью перекинутой через блок, закрепленный на потолке. Найдите ускорение грузов и силы натяжения нити в месте крепления к грузам. Блок и нити невесомы, трение отсутствует.
Задача 5
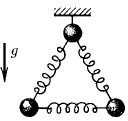
Система из трех одинаковых шаров, связанных одинаковыми пружинами, подвешена на нити к потолку и находится в равновесии. Нить перерезают, найдите ускорения шаров сразу после перерезания нити.
Задача 6
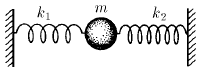Тело массы m, с разных сторон, соединено двумя пружинами жесткости k 1 и k 2 с неподвижными стенками, пружины первоначально не деформированы. При возникновении колебаний, наибольшее ускорение тела равно a. Найдите максимальное отклонение тела от положения равновесия и максимальные силы, с которыми пружины действуют на стенки.
Задача 7
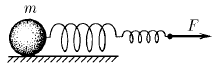Тело массы m прикреплено к двум соединенным последовательно пружинам жесткости k 1 и k 2. К свободному концу цепочки пружин приложена постоянная сила F. Каково суммарное удлинение пружин, если движение системы установилось (колебания прекратились)?
Занятие 2
Задача 8
Тело, находящееся на горизонтальной плоскости, тянут за нить в горизонтальном направлении. Нарисуйте график зависимости силы трения, действующей на тело со стороны плоскости, от силы натяжения нити. Первоначально тело неподвижно. Масса тела равна 10 кг, а коэффициент трения 0,51.
Задача 9
Ленточный подъемник образует угол α с горизонтом. С каким максимальным ускорением может подниматься ящик на таком подъемнике, если коэффициент трения равен μ? Лента подъемника не прогибается.
Задача 10
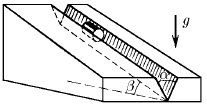Цилиндр скользит по желобу, имеющему вид двугранного угла с раствором α. Ребро двугранного угла наклонено под углом β к горизонту. Плоскости двугранного угла образуют одинаковые углы с горизонтом. Определите ускорение цилиндра. Коэффициент трения между цилиндром и поверхностью желоба μ.
Задача 11
По деревянным сходням, образующим угол α с горизонтом втаскивают за привязанную к нему веревку массивный ящик. Коэффициент трения ящика о сходни μ. Под каким углом к горизонту следует тянуть за веревку, чтобы с наименьшим усилием втащить ящик?
Задача 12
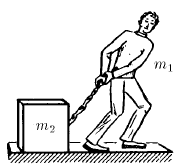Человек массы m 1, оставаясь на месте, тянет за веревку груз массы m 2. Коэффициент трения о горизонтальную плоскость равен μ. При какой наименьшей силе натяжения веревки груз сдвинется с места? Различием в сопротивлении трения покоя и скольжения пренебречь.
Задача 13
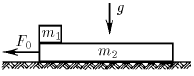Тело массы m 1 лежит на доске массы m 2, находящейся на гладкой горизонтальной плоскости. Коэффициент трения между телом и доской μ. Какую силу нужно приложить к доске, чтобы тело соскользнуло с нее? За какое время тело соскользнет, если к доске приложена сила F 0, а длина доски равна L? С каким ускорением будут двигаться тело и доска, если сила F 0 приложена к телу массы m 1?
Занятие 3
Задача 14
Масса воздушного шара вместе с канатом, волочащимся по земле, равна m; выталкивающая сила, действующая на шар, равна F; коэффициент трения каната о землю равен μ. Сила сопротивления воздуха, действующая на воздушный шар, пропорциональна квадрату скорости шара относительно воздуха и равна α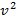 
. Найдите скорость шара относительно земли, если дует горизонтальный ветер со скоростью u.
Задача 15
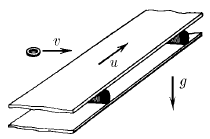Лента горизонтального транспортера движется со скоростью u. На ленту по касательной к ней влетает шайба, начальная скорость v которой перпендикулярна краю ленты. Найдите максимальную ширину ленты, при которой шайба достигнет другого ее края, если коэффициент трения между шайбой и лентой μ.
Задача 16
Какая шайба, вращающаяся вокруг своей или не вращающаяся пройдет больший путь до остановки? Начальная скорость центров шайб одинакова.
Задача 17
Горизонтальную ось радиуса R, вращающуюся с угловой скоростью ω, обжимает втулка, снабженная противовесом, чтобы перемещаясь вдоль оси, она не вращалась. Определите установившуюся скорость втулки под действием силы F, приложенной к ней вдоль оси. Максимальная сила трения оси о втулку F тр > F.
Задача 18
На плоскости, тангенс угла наклона которой равен коэффициенту трения, лежит монетка. В горизонтальном направлении вдоль плоскости монете сообщили скорость v. Найдите установившуюся скорость монеты.
Занятие 4
Задача 19
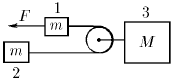Найдите ускорение тел системы изображенной на рисунке. Сила F приложена в направлении нити к одному из тел массы m. Участки нити по обе стороны от легкого блока, прикрепленного к телу массы M, параллельны.
Задача 20
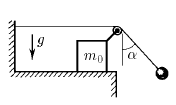
К свободному концу нити, прикрепленной к стенке и переброшенной через ролик, подвешен груз. Ролик закреплен на бруске массы m 0, который может скользить по горизонтальной плоскости без трения. В начальный момент нить с грузом отклоняют на угол α от вертикали, а затем отпускают. Определите ускорение бруска, если известно, что угол, образованный нитью с вертикалью, не меняется при движении системы. Чему равна масса груза?
Задача 21
Скорость тела массы m в жидкости убывает с пройденным расстоянием l по закону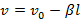 
, где 
– начальная скорость, а β – постоянный коэффициент. Как зависит сила вязкого трения, действующая на тело со стороны жидкости, от скорости тела?
Задача 22
Сила сопротивления воздуха, действующая на капли дождя, пропорциональна произведению квадрата скорости капель на квадрат их радиуса: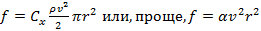 
, где ρ – плотность воздуха, а безразмерный коэффициент 
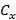равен приблизительно 0,16 (а α 0,3). Какие капли, крупные или мелкие, падают на землю с большей скоростью? Оцените скорость капли радиусом в 1 мм при падении с большой высоты.
Задача 23
Сила сопротивления воздуха, действующая на капли тумана, пропорциональна произведению радиуса на скорость: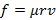 
. Капли радиуса 0,1 мм падая с большой высоты имеют скорость порядка 1 м/с. Какую скорость будут иметь капли, радиус которых в два раза меньше? А в десять раз?
Занятие 5
Задача 24
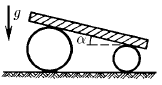
На два катка разного радиуса положи тяжелую плиту. Она образует угол α с горизонтом. Найдите ускорение этой плиты. Проскальзывания нет. Масса катков в сравнении с массой плиты мала.
Задача 25
Тело массы M связано нитью длины l с осью, вокруг которой оно обращается с угловой скоростью ω. Найдите силу натяжения нити. Размером тела и силой тяжести пренебречь. Замените нить однородной веревкой массы m и найдите зависимость силы натяжения веревки от расстояния x от оси вращения.
Задача 26
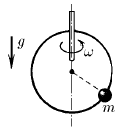На гладкое проволочное кольцо радиуса R, расположенное вертикально, надета маленькая бусинка массы m, которая может скользить по кольцу без трения. Кольцо вращается с угловой скоростью ω вокруг вертикальной оси, проходящей по диаметру кольца. Где находится бусинка?
Задача 27
Из тонкого резинового жгута массы m и жесткости k сделали кольцо радиуса R 0. Это кольцо раскрутили вокруг его оси. Найдите новый радиус кольца, если угловая скорость его вращения ω.
Занятие 6
Задача 28
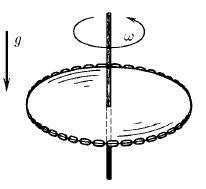
Кольцевая цепочка массы m надета на горизонтальный диск радиуса R. Сила натяжения надетой цепочки равна T. Найдите коэффициент трения между диском и цепочкой, если при вращении диска с угловой скоростью равной или большей ω, цепочка с него спадает.
Задача 29
Конькобежец на ледяной дорожке старается пройти вираж как можно ближе к внутренней бровке. Велосипедист на велотреке, наоборот, проходит вираж как можно дальше от внутренней бровки. Как объяснить это различие в тактике прохождения виража? Профиль велотрека все круче по мере удаления от внутренней бровки.
Задача 30
В цирковом аттракционе мотоциклист движется по внутренней поверхности сферы радиуса R. Разогнавшись, он начинает описывать горизонтальную окружность в верхней полусфере. После этого, для пущего эффекта нижнюю полусферу убирают. Определите минимальную скорость мотоциклиста, если коэффициент трения шин о поверхность сферы равен μ, а угол между вертикалью и направлением к мотоциклисту из центра сферы равен α.
Задача 31
С какой угловой скоростью должен вращаться вокруг своей оси горизонтально расположенный цилиндр, чтобы мелкие частицы внутри цилиндра не соскальзывали с его поверхности? Коэффициент трения между поверхностью цилиндра и частицами µ=1, внутренний радиус цилиндра R.
Импульс. Центр масс.
Занятие 1
Задача 1
Частица массы m движется со скоростью v, а частица массы 2 m движется со скоростью 2 v в направлении, перпендикулярном направлению движения первой частицы. На каждую частицу начинают действовать одинаковые силы. После прекращения действия сил первая частица движется со скоростью 2 v в направлении, обратном первоначальному. Определить скорость второй частицы.
Задача 2
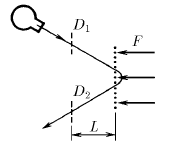В масс-пролетном спектрометре источник испускает сгусток заряженных частиц, которые сначала летят свободно, и пролетают первый датчик D 1, находящийся на расстоянии L от сетки. За сеткой, по нормали к ней, на частицы действует электрическая сила F. Частицы поворачиваются и вылетают через сетку назад, пролетая через второй датчик D 2, находящийся на том же расстоянии от сетки. От напряжения источника зависит скорость вылетающих частиц, но точное ее значение остается неизвестным. Меняя напряжения, измеряют время между срабатываниями датчиков и находят наименьшее его значение Δ t. Какова масса частицы? Как можно найти массу частиц, если источник испускает несколько сортов частиц с разной массой?
Задача 3
Ящик с песком массы M лежит на горизонтальной плоскости, коэффициент трения с которой равен µ. Под углом α к вертикали в ящик со скоростью v влетает пуля массы m и почти мгновенно застревает в песке. Через какое время после попадания пули в ящик, он, начав движение, остановится? При каком значении α он вообще не сдвинется?
Задача 4
При наблюдениях с Земли удается определить только радиальную скорость звезд-партнеров, входящих в состав двойной звезды. При измерениях получены значения радиальной скорости v 1 и u 1 звезд партнеров двойной звезды. При повторных измерениях, проведенных через год, значения этой скорости составили v 2 и u 2. Найдите отношения масс звезд, входящих в состав двойной звезды. Почему нужно изменить расчеты, если повторное измерение проводится через день, месяц или полгода?
Задача 5
На покоящееся тело массы m 1 налетает со скоростью v тело массы m 2. Сила, возникающая при взаимодействии тел, линейно зависящая от времени, растет от нуля до значения F 0 за время t 0, а затем равномерно убывает до нуля за то же время. Определите скорости тел после взаимодействия, считая, что движение происходит по одной прямой.
Задача 6
Космический корабль перед отделением последней ступени ракеты-носителя имел скорость v, после отбрасывания последней ступени его скорость стала равной 1.01 v, при этом отделившаяся ступень удаляется от корабля со скоростью 0.04 v. Какова масса последней ступени, если масса корабля m 0?
Задача 7
Протон с начальной скоростью v летит прямо на первоначально покоящееся ядро гелия. Какова скорость частиц при наибольшем их сближении? Масса ядра гелия близка к учетверенной массе протона.
Задача 8
При β-распаде покоящегося первоначально нейтрона образуются протон, электрон и нейтрино. Импульсы протона и электрона равны p 1 и p 2, угол между ними α. Определите импульс нейтрино.
Занятие 2
Задача 9
Где находится центр масс однородного прута, согнутого посередине под прямым углом? Однородной треугольной пластинки?
Задача 10
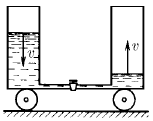На первоначально неподвижной тележке установлены два вертикальных цилиндрических сосуда, соединенных тонкой трубкой. Площадь сечения каждого сосуда равна S, расстояние между их осями l. Один из сосудов заполнен жидкостью плотности ρ. Кран на соединительной трубке открывают. Найдите скорость тележки в момент времени, когда скорость уровня жидкости равна v. Полная масса системы равна m.
Задача 11
На гладком полу стоит сосуд заполненный водой плотности ρ 0, объем воды в сосуде V 0. Оказавшийся на дне сосуда жук объема V и плотности ρ начинает ползти по дну сосуда со скоростью u относительно него. С какой скоростью станет двигаться сосуд по полу? Массой сосуда пренебречь, уровень воды все время остается горизонтальным.
Задача 12
Два тела массы m 1 и m 2 связаны натянутой нитью длины l и движутся по гладкой горизонтальной поверхности. В некоторый момент времени оказалось, что тело массы m 1 неподвижно, а другое тело движется со скоростью v перпендикулярно нити. Определите силу натяжения нити.
Задача 13
Космическая станция состоит из двух отсеков массы m 1 и m 2, соединенных длинным однородным тросом длины L. Станция вращается вокруг своей оси, перпендикулярной тросу. Какова угловая скорость вращения, если сила натяжения троса вблизи первого отсека равна T 1, а вблизи второго T 2? Какова масса троса?
Задача 15
Три точечные массы m 1, m 2, m 3 связаны нитями длины l и вращаются с угловой скоростью ω вокруг центра масс сохраняя конфигурацию равностороннего треугольника. Найдите силу натяжения всех нитей.
Занятие 3
Задача 16
На тележке установлен цилиндрический сосуд с площадью сечения S, наполненный жидкостью плотности ρ. От сосуда, параллельно полу, отходит тонкая горизонтальная трубка длины L, небольшой отрезок которой загнут по вертикали вниз. Уровень жидкости в сосуде опускается с ускорением a. Какой горизонтальной силой можно удержать тележку на месте?
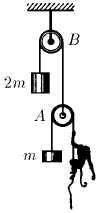
Задача 17
Обезьяна массы m уравновешена противовесом на блоке A. Блок A уравновешен грузом массы 2 m на блоке B. В исходном состоянии система неподвижна. Обезьяна начинает равномерно выбирать веревку со скоростью u относительно себя. Как будут двигаться грузы? Массой блоков и трением пренебречь.
Задача 18
На тросе висит небольшой ящик с песком. В ящик стреляют из пулемета и пули застревают в песке. Скорость пули v, масса пули m, масса ящика с песком M. Трос отклоняется на угол α от вертикали. Какова скорострельность пулемета, если все выпущенные пули попадают в цель?
Задача 19
В цилиндре под поршнем массы M прыгают, упруго ударяясь о поршень и дно цилиндра, N >>1 шариков массы m каждый. Сила тяжести, действующая на поршень, уравновешена ударами шариков. Расстояние между дном цилиндра и поршнем равно h. Полная энергия каждого шарика одинакова. На какую высоту будут подскакивать шарики, если поршень мгновенно убрать (за время поднятия поршня не произойдет столкновений между шариками и поршнем)?
Задача 20
Две тележки массы M каждая движутся параллельно со скоростям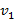и 
и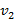 
. Груз массы m, сначала лежавший на первой тележке, с почти нулевой скоростью относительно этой тележки перебрасывают на вторую тележку. Затем с почти нулевой скоростью уже относительно второй тележки его перебрасывают обратно на первую. Какой станет разность скоростей тележек после N таких перебросов груза туда и обратно?
Задача 21
Веревку, перекинутую через гладкий гвоздь, протаскивают со скоростью v сквозь щель. Сила трения в щели F, масса единицы длины веревки ρ. Определите силу, действующую на гвоздь, если участки веревки по разные стороны гвоздя образуют угол α. При какой скорости веревка отойдет от гвоздя?
Задача 22
Газ, вытекающий из сопла ракеты, имеет скорость v относительно нее. Определите изменение скорости ракеты после того, как ее масса из-за истечения газа уменьшилась в n раз.
Дата: 2018-12-28, просмотров: 388.
