Задача 140
Определите радиус круговой орбиты астероида, если угловая скорость обращения его вокруг Солнца ω, а масса Солнца  .
.
Ответ: 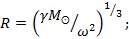
Задача 141
Спутник массы 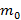 движется по круговой орбите радиуса R вокруг планеты массы m. Какой импульс нужно мгновенно сообщить спутнику, чтобы плоскость его орбиты повернулась на угол α, а радиус остался прежним?
движется по круговой орбите радиуса R вокруг планеты массы m. Какой импульс нужно мгновенно сообщить спутнику, чтобы плоскость его орбиты повернулась на угол α, а радиус остался прежним?
Ответ: 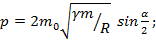
Задача 142
Космический корабль движется по круговой орбите радиуса R вокруг Земли со скоростью v, вдвое большей скорости свободного движения по той же орбите. Какую силу тяги развивают двигатели корабля, если его масса m?
Ответ: 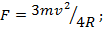
Задача 143
Какую скорость нужно сообщить телу небольшой массы в центре астероида массы m и радиуса R, чтобы оно через радиальную шахту ушло от астероида бесконечно далеко?
Ответ: 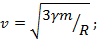
Задача 144
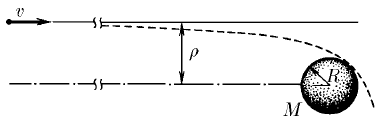 К планете радиуса R и массы M издалека движется со скоростью v относительно нее космический зонд. При каком прицельном параметре ρ зонд пролетит ближе всего к планете, не разбившись?
К планете радиуса R и массы M издалека движется со скоростью v относительно нее космический зонд. При каком прицельном параметре ρ зонд пролетит ближе всего к планете, не разбившись?
Ответ: 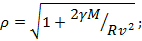
Задача 145
Спутник, двигавшийся по круговой орбите радиуса 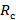 был мгновенно заторможен и стал двигаться по эллиптической орбите, касающейся начальной орбиты и поверхности планеты. Определите время падения спутника на планету. Радиус планеты R, ускорение свободного падения на поверхности планеты g.
был мгновенно заторможен и стал двигаться по эллиптической орбите, касающейся начальной орбиты и поверхности планеты. Определите время падения спутника на планету. Радиус планеты R, ускорение свободного падения на поверхности планеты g.
Ответ: 
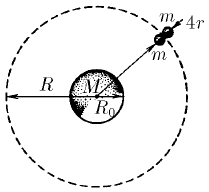 Задача 146
Задача 146
Две соприкасающиеся шаровые глыбы массы m и радиуса r каждая движутся по круговой орбите вокруг планеты массы M. Центры глыб находятся на одном радиусе, расстояние от точки соприкосновения до центра планеты R. С какой силой одна глыба давит на другую? При каком радиусе орбиты взаимное притяжение глыб перестанет удерживать их вместе? Плотность глыб и планеты одинакова.
Ответ: 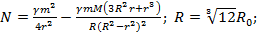
Статика
 Задача 147
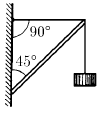
Задача 147
К стене под углом 90° прикреплена балка. Через свободный конец балки перекинут трос, который закреплен к стене на одной высоте с со свободным концом балки. За второй конец троса подвешен груз массы m. Найдите силу действующую на балку со стороны троса. Трением пренебречь.
Ответ
 Задача 148
Задача 148
Два груза небольшого размера соединены нитью длины l и лежат на цилиндрической гладкой поверхности радиуса R. При равновесии грузов угол между вертикалью и радиусом, проведенным к грузу массы 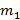 , равен α. Найдите массу второго груза.
, равен α. Найдите массу второго груза.
Ответ: 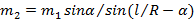
 Задача 149
Задача 149
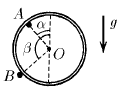
Гладкий тонкий обруч массы m висит у стенки на одном гвозде (А) и опирается на другой (B). Радиус, проведенный к гвоздю А из центра обруча, образует угол α с вертикалью. Радиус, проведенный к гвоздю B, образует угол β с вертикалью. Найдите, с какой силой действует обруч на каждый гвоздь.
Ответ: 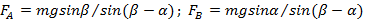
Задача 150
На цилиндрический столб намотан один виток каната. Чтобы канат не скользил по столбу, когда его за один из концов тянут с силой F, другой конец каната достаточно удерживать с силой f. Как изменится удерживающая сила, если на столб намотано n витков? Витки каната не соприкасаются друг с другом.
Ответ: 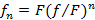
Задача 151
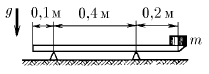 Линейка массы 10 г лежит на двух опорах так, как это показано на рисунке. На один конец линейки положен груз. Какова масса груза, при которой возможно равновесие?
Линейка массы 10 г лежит на двух опорах так, как это показано на рисунке. На один конец линейки положен груз. Какова масса груза, при которой возможно равновесие?
Ответ: 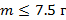
 Задача 152
Задача 152
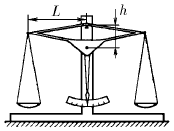
Центр масс коромысла равноплечих весов находится ниже точки подвеса на расстоянии h от нее, а масса коромысла равна 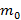 . На концах коромысла, расстояние между которыми равно 2 L, на нитях подвешены одинаковые чашки. На сколько отличаются массы грузов, положенных на чашки, если коромысло отклонилось на угол α?
. На концах коромысла, расстояние между которыми равно 2 L, на нитях подвешены одинаковые чашки. На сколько отличаются массы грузов, положенных на чашки, если коромысло отклонилось на угол α?
Ответ: 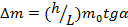
Задача 153
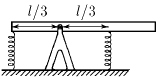 Однородная балка длины l и массы m на расстоянии l /3 от конца имеет ось вращения. К концу балки присоединена пружина, прикрепленная к полу, и такая же пружина присоединена симметрично по другую сторону оси. При горизонтальном положении балки обе пружины не деформированы. Найдите силы, с которыми балка действует на ось и пружины. Деформации пружин малы, балка практически горизонтальна.
Однородная балка длины l и массы m на расстоянии l /3 от конца имеет ось вращения. К концу балки присоединена пружина, прикрепленная к полу, и такая же пружина присоединена симметрично по другую сторону оси. При горизонтальном положении балки обе пружины не деформированы. Найдите силы, с которыми балка действует на ось и пружины. Деформации пружин малы, балка практически горизонтальна.
Ответ: 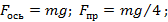
 Задача 154
Задача 154
Найдите силу натяжения нити, связывающей оси шарниров верхнего ромба легкой шарнирной подвески. Масса груза m.
Ответ: 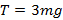
 Задача 155
Задача 155
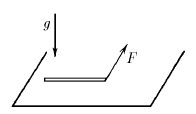
Однородный тонкий брусок массы m лежит на горизонтальной плоскости. Какой наименьший горизонтальной силой, приложенной к концу бруска по перпендикуляру к нему, его можно стронуть с места, если коэффициент трения между бруском и плоскостью равен µ?
Ответ: 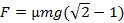
Для олимпиадников:
· 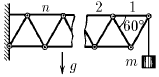 (156) К системе одинаковых стержней, соединенных шарнирами, подвешен груз массы m, как показано на рисунке. Определите силу, растягивающую n-й верхний горизонтальный стержень.
(156) К системе одинаковых стержней, соединенных шарнирами, подвешен груз массы m, как показано на рисунке. Определите силу, растягивающую n-й верхний горизонтальный стержень.
 Ответ:
Ответ:
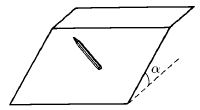
· (157) На парту с углом наклона поверхности  кладут шестигранный карандаш так, чтобы он не скатился вниз и не скользил. При каком наименьшем угле между осью карандаша и горизонтальным краем парты это возможно?
кладут шестигранный карандаш так, чтобы он не скатился вниз и не скользил. При каком наименьшем угле между осью карандаша и горизонтальным краем парты это возможно?
Ответ
Механика жидкости.
Давление жидкости.
 Задача 158
Задача 158
В жидкости находится прямоугольная призма, размеры которой показаны на рисунке. Найдите сумму сил, действующих на переднюю и нижнюю грани призмы, если давление жидкости равно  . Чему равна сумма сил, действующих на призму?
. Чему равна сумма сил, действующих на призму?
Ответ: очевиден
Задача 159
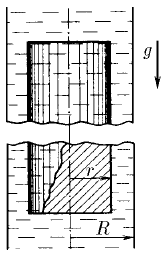
 В трубе радиуса r находится поршень, продольное сечение которого показано на рисунке, угол при основании α. Давление жидкости с обеих сторон поршня одинаково и равно P. Найдите сумму сил, действующих на поршень в направлении оси трубы. При каком значении коэффициента трения между поршнем и трубой, поршень не будет двигаться?
В трубе радиуса r находится поршень, продольное сечение которого показано на рисунке, угол при основании α. Давление жидкости с обеих сторон поршня одинаково и равно P. Найдите сумму сил, действующих на поршень в направлении оси трубы. При каком значении коэффициента трения между поршнем и трубой, поршень не будет двигаться?
 Ответ: очевиден
Ответ: очевиден
Задача 160
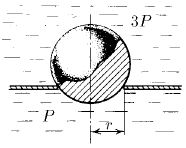
Шар перекрывает отверстие радиуса r в плоской стенке, разделяющей жидкости, давление которых равно 3P и P. С какой силой прижимается шар к отверстию?
Ответ: тоже слишком просто для наличия ответа
Задача 161
Почему сосиска в кипятке лопается вдоль, а не поперек?
Ответ: не могу подсказать
 Задача 162
Задача 162
Три сообщающихся сосуда с водой прикрыты поршнями. К поршням шарнирно прикреплена на вертикальных стержнях горизонтальная палка. В каком месте нужно приложить к палке силу F, чтобы она осталась горизонтальной? Диаметры сосудов и расстояния между ними даны на рисунке.
Ответ:  слева от центра палки
слева от центра палки
 Задача 163
Задача 163
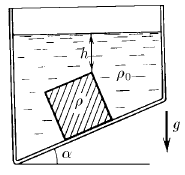
В сосуде, дно которого образует угол α с горизонтом, стоит куб с ребром a, сделанный из материала плотности ρ. Верхнее ребро куба находится на глубине h. Жидкость под основание куба не подтекает. Атмосферное давление P. Плотность жидкости 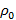 . Найдите силу, с которой куб действует на дно сосуда.
. Найдите силу, с которой куб действует на дно сосуда.
Ответ: 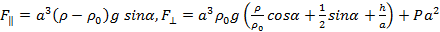
 Задача 164
Задача 164
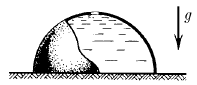
В полусферический колокол с внутренним радиусом R, края которого плотно прилегают к поверхности стола, наливают через отверстие вверху жидкость плотности ρ. Когда жидкость доходит до отверстия, она приподнимает колокол и начинает из-под него течь. Найдите массу колокола.
Ответ: 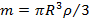
Задача 165
Докажите, что в двух сообщающихся сосудах жидкость в поле тяжести имеет минимальную потенциальную энергию, когда уровни жидкости в обоих сосудах находятся на одной высоте.
Задача 166
Найдите давление на расстоянии r от центра жидкой планеты радиуса R, если жидкость имеет плотность ρ. Чему равно давление в центре планеты? Гравитационная постоянная равна G.
Ответ: 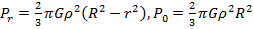
Задача 167
В сосуде с жидкостью находится газовый пузырь. Поля тяжести нет. Сосуд начинает двигаться с постоянным ускорением. Куда начнет двигаться пузырь?
Ответ: очевидно
Задача 168
Найдите форму поверхности жидкости в вертикально расположенном цилиндрическом стакане, который вращается вместе с жидкостью вокруг своей оси с угловой скоростью ω.
Ответ: 
Закон Архимеда.
 Задача 169
Задача 169
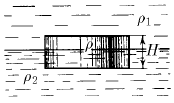
На границе раздела двух жидкостей плотности 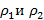 плавает шайба плотности ρ (
плавает шайба плотности ρ (  ). Высота шайбы H. Определите глубину ее погружения в нижнюю жидкость.
). Высота шайбы H. Определите глубину ее погружения в нижнюю жидкость.
Ответ: 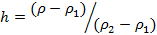
Задача 170
Тело в воде весит в три раза меньше, чем в воздухе, чему равна плотность тела?
Ответ: просто
Задача 171
К коромыслу весов подвешены два груза равной массы. Если один из грузов поместить в жидкость плотности 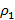 , а другой в жидкость плотности
, а другой в жидкость плотности 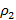 , то равновесие сохраняется. Найдите соотношение плотностей грузов.
, то равновесие сохраняется. Найдите соотношение плотностей грузов.
Ответ: элементарно
Задача 172
В сообщающиеся сосуды диаметра 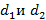 налита жидкость плотности ρ. На сколько поднимется уровень жидкости в сосудах, если в один из сосудов положить тело массы m из материала, плотность которого меньше ρ?
налита жидкость плотности ρ. На сколько поднимется уровень жидкости в сосудах, если в один из сосудов положить тело массы m из материала, плотность которого меньше ρ?
Ответ: 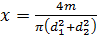
 Задача 173
Задача 173
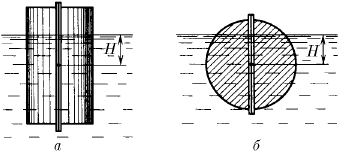
Как зависит сила, прижимающая друг к другу два одинаковых полуцилиндра плавающего батискафа, от глубины его погружения H, если он плавает на поверхности жидкости так, как это показано на рисунках а и б? Радиус батискафа R, длина L, плотность жидкости ρ.
 Ответ:
Ответ: 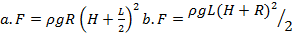
Задача 174
Докажите, что сила, с которой прижимаются половины плавающего батискафа друг к друга, не зависит от наклона плоскости соприкосновения полусфер батискафа, если он полностью погружен в воду.
 Задача 175
Задача 175
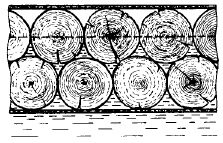
Определите минимальную силу натяжения двух канатов, связывающих широкий плот, состоящий из двух слоев бревен. Масса каждого бревна m. Верхний слой бревен погружен в воду наполовину. 4.2.20
Ответ: 
Задача 176
Какое количество теплоты выделится в водоеме при всплывании в нем воздушного пузыря радиуса R с глубины H? Плотность жидкости ρ.
Ответ: 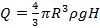
Задача 177
Какую минимальную работу нужно произвести, чтобы поднять со дна моря на борт судна батисферу радиуса R и массы m? Глубина моря H, высота борта судна h. Плотность морской воды ρ.
Задача 178
Цилиндрический космический корабль радиуса R вращается вокруг своей оси с угловой скоростью ω. Бассейн в корабле имеет глубину H, а дном бассейна служит боковая стенка корабля. Определите плотность плавающей в бассейне палочки длины 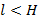 , если из воды выступает ее верхняя часть длины Δ.
, если из воды выступает ее верхняя часть длины Δ.
Ответ: 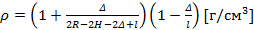
Задача 179
Вертикальный цилиндрический сосуд радиуса R, частично наполненный жидкостью, вращается вокруг своей оси. К боковой стенке сосуда на нити длины l привязан воздушный шарик радиуса r; во время вращения нить образует со стенкой угол α. Определите угловую скорость вращения сосуда.
Ответ: 
Задача 180
Молекула жидкости состоит из двух слабо связанных групп атомов. Объем этих групп одинаков, их массы равны 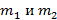 . При вращении жидкости в центрифуге радиуса R с угловой скоростью, большей ω, молекулы начинают распадаться. Оцените силу связи групп атомов.
. При вращении жидкости в центрифуге радиуса R с угловой скоростью, большей ω, молекулы начинают распадаться. Оцените силу связи групп атомов.
Ответ: 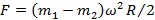
Течение идеальной жидкости.
Задача 181
Насос должен подавать ежесекундно объем воды V на высоту h по трубе постоянного сечения S. Какова должна быть мощность насоса? Плотность воды ρ.
Ответ: 
Задача 182
Насос представляет собой расположенный горизонтально цилиндр с поршнем площади S и выходным отверстием площади s, расположенным на оси цилиндра. Определите скорость истечения струи жидкости из насоса, если поршень под действием силы F перемещается с постоянной скоростью. Плотность жидкости ρ.
Ответ: 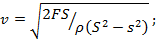
Задача 183
 Плита массы m удерживается на месте в горизонтальном положении N струями жидкости плотности ρ, бьющими вертикально вверх. Площадь каждого отверстия S. Скорость жидкости на выходе из отверстий v. На какой высоте над отверстиями удерживается плита, если, достигнув плиты, жидкость разлетается от нее в горизонтальной плоскости?
Плита массы m удерживается на месте в горизонтальном положении N струями жидкости плотности ρ, бьющими вертикально вверх. Площадь каждого отверстия S. Скорость жидкости на выходе из отверстий v. На какой высоте над отверстиями удерживается плита, если, достигнув плиты, жидкость разлетается от нее в горизонтальной плоскости?
Ответ: 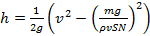
Задача 184
С каким ускорением будет двигаться длинное цилиндрическое тело плотности ρ и радиуса r вдоль оси вертикального высокого цилиндрического сосуда радиуса R, заполненного жидкостью плотности 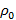 ? Чему равна разность давлений на верхнее и нижнее основания тела, если его длина равна h?
? Чему равна разность давлений на верхнее и нижнее основания тела, если его длина равна h?
Ответ: 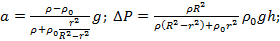
 Задача 185
Задача 185
Во сколько раз увеличится сброс воды через широкую плотину, если высота уровня воды над кромкой возрастет в два раза?
Ответ: 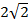
 Задача 186
Задача 186
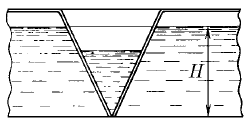
Вода вытекает из широкого сосуда через треугольный вырез в его стенке. Во сколько раз уменьшится скорость понижения уровня жидкости при изменении высоты ее уровня от H до h?
Ответ: 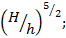
 Задача 187
Задача 187
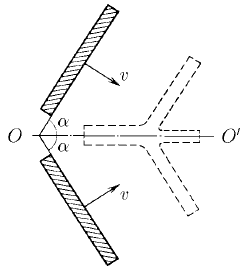
Две широкие металлические пластины, расположенные под углом 2α друг к другу, движутся со скоростью v по нормали к своей поверхности. Найдите скорость струй, возникающих при столкновении пластин, рассматривая движение металла как движение идеальной жидкости.
Ответ: 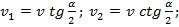
Задача 188
Определите форму стационарной струи, сформировавшейся после столкновения двух струй радиуса R и r, которые двигались навстречу друг другу с одинаковой скоростью.
Ответ: 
Течение вязкой жидкости.
Задача 189
Пространство между двумя параллельными плоскостями заполнено жидкостью вязкости η. Одна из плоскостей движется со скоростью 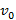 , другая покоится. Расстояние между плоскостями h. Найдите:
, другая покоится. Расстояние между плоскостями h. Найдите:
а. распределение скорости жидкости между плоскостями (или, хотя бы градиент);
б. силу вязкого трения, действующую на единицу площади каждой из плоскостей.
Ответ: 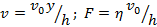 ;
;
Задача 190
Из вертикально расположенной трубки, заполненной вязкой жидкостью, через время T вытекла половина жидкости. Через какое время вытечет оставшаяся часть жидкости?
Ответ: думаем
Задача 191
Пространство между валом радиуса r, вращающегося вокруг своей оси и неподвижной соосной с валом трубой радиуса R заполнено жидкостью вязкости η. Момент сил, действующих на единицу длины вала, равен M. Определите зависимость от расстояния до оси вала:
а. градиента угловой скорости жидкости;
б. угловой скорости жидкости. Угловую скорость вала.
Ответ: 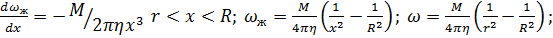
Дата: 2018-12-28, просмотров: 786.