Определение производной
Определение 2.1: Производной функции 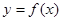 по аргументу x называется предел отношения ее приращения
по аргументу x называется предел отношения ее приращения 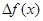 к приращению
к приращению 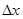 аргумента x, когда приращение аргумента стремится к нулю:
аргумента x, когда приращение аргумента стремится к нулю:
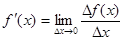 .
.
Если этот предел конечный, то функция y=f(x) называется дифференцируемой в точке x. Если же этот предел есть ∞, то говорят, что функция y=f(x) имеет в точке x бесконечную производную.
Механический смысл производной: скорость есть первая производная пути по времени, т.е. 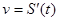 .
.
Геометрический смысл производной: тангенс угла наклона касательной к графику функции 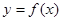 равен первой производной этой функции , вычисленной в точке касания, т.е.
равен первой производной этой функции , вычисленной в точке касания, т.е. 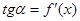
Уравнение касательной к графику функции 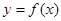 в точке
в точке 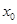 :
:
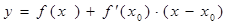
Уравнение нормали к графику функции 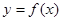 в точке
в точке 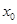 :
:
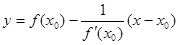
Таблица производных
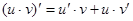
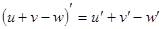
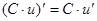
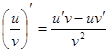
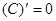
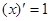
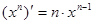
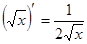
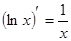
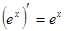
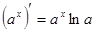
| 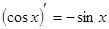
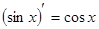
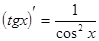
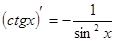
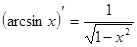
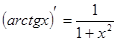
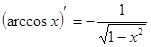
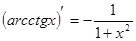
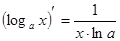
|
Процесс нахождения производных называется дифференцированием функции.
Найти производные функций:
Пример 1: 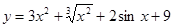
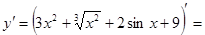
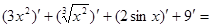
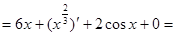
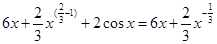 +
+
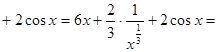
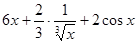
Пример2: 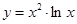
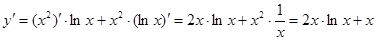
Пример 3: 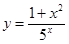
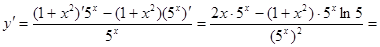
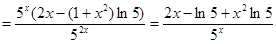
Дифференцирование сложной функции
Пусть y = y ( u ) , где u = u ( x ) – дифференцируемые функции. Тогда сложная функция y = y [ u ( x )] есть также дифференцируемая функция.
Производные сложных функций находятся при помощи таблицы:
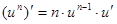
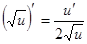
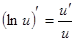
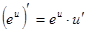
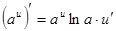
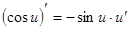
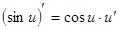
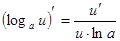
| 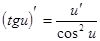
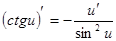
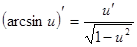
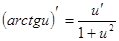
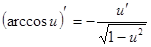
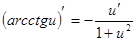
|
Рассмотрим примеры.
Пример 1: Найти производную функции 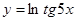
Решение: 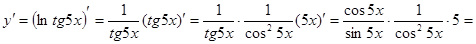 =
= 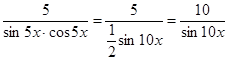
Пример 2: Найти производную функции 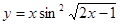
Решение: 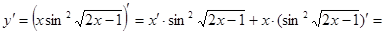
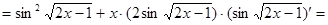
= 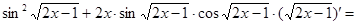
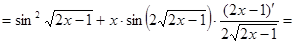
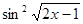 +
+
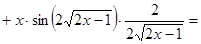
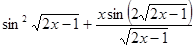
Производные высших порядков
Определение2.2: Производная второго порядка (вторая производная) от функции y=f(x) есть производная от ее первой производной: 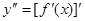 .
.
Определение 2.3 : Производная третьего порядка (третья производная) от функции y=f(x) есть производная от ее второй производной: 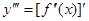 .
.
Определение 2.4 : Производная n -ого порядка (n-я производная) от функции y = f ( x ) есть производная от ее (n -1)-й производной: 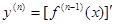 .
.
Рассмотрим примеры.
Пример 1: Найти производную второго порядка 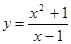 .
.
Решение: 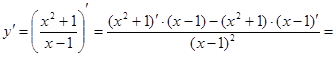
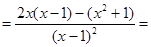
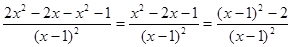
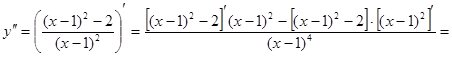
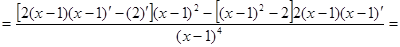
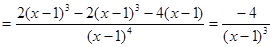
Пример2: Найти производную второго порядка функции 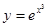 .
.
Решение: 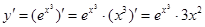
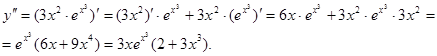
Исследование функции с помощью производной
Определение 2.5: Точка х0 называется точкой локального максимума, если для любого х из окрестности точки х0 выполняется неравенство:
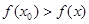 .
.
Определение 2.6: Точка х0 называется точкой локального минимума, если для любого х из окрестности точки х0 выполняется неравенство:
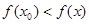 .
.
Точки минимума и максимума функции называются точками экстремума данной функции, а значения функции в этих точках – экстремумами функции.
Точками экстремума могут служить только критические точки I рода, т.е. точки, принадлежащие области определения функции, в которых производная 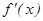 обращается в нуль или терпит разрыв.
обращается в нуль или терпит разрыв.
Правило нахождения экстремумов функции 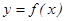
Дата: 2018-12-28, просмотров: 323.