Раздел I Линейная алгебра
Тема 1. Матрицы и определители
Определение 1.1. Матрицей называется прямоугольная таблица чисел.
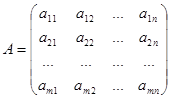
Обозначения: А – матрица, 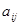 - элемент матрицы,
- элемент матрицы, 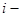 номер строки, в которой стоит данный элемент,
номер строки, в которой стоит данный элемент, 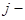 номер соответствующего столбца; m – число строк матрицы, n – число ее столбцов.
номер соответствующего столбца; m – число строк матрицы, n – число ее столбцов.
Определение 1.2. Числа m и n называются размерностями матрицы.
Определение 1.3. Матрица называется квадратной, если m = n. Число n в этом случае называют порядком квадратной матрицы.
Каждой квадратной матрице можно поставить в соответствие число, определяемое единственным образом с использованием всех элементов матрицы. Это число называется определителем.
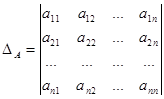
Определение 1.4. Определителем второго порядка называется число, полученное с помощью элементов квадратной матрицы 2-го порядка следующим образом:
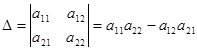 .
.
При этом из произведения элементов, стоящих на так называемой главной диагонали матрицы (идущей из левого верхнего в правый нижний угол) вычитается произведение элементов, находящихся на второй, или побочной, диагонали.
Примеры:
1. 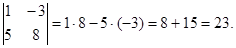 2.
2. 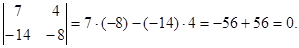
Определение 1.5. Определителем третьего порядка называется число, определяемое с помощью элементов квадратной матрицы 3-го порядка следующим образом:
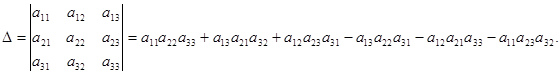
Замечание. Для того, чтобы легче запомнить эту формулу, можно использовать так называемое правило треугольников. Оно заключается в следующем: элементы, произведения которых входят в определитель со знаком «+», располагаются так:














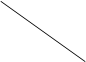
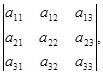 образуя два треугольника, симметричных относительно главной диагонали. Элементы, произведения которых входят в определитель со знаком «-», располагаются аналогичным образом относительно побочной диагонали:
образуя два треугольника, симметричных относительно главной диагонали. Элементы, произведения которых входят в определитель со знаком «-», располагаются аналогичным образом относительно побочной диагонали: 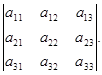
 Примеры.
Примеры.
1. 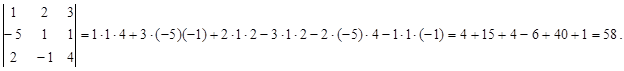
2. 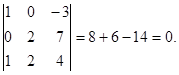
Определение1. 6. Транспонированием матрицы называется операция, в результате которой меняются местами строки и столбцы с сохранением порядка их следования. В результате получается матрица А`, называемая транспонированной по отношению к матрице А, элементы которой связаны с элементами А соотношением a ` ij = aji .
Правило Крамера.
Рассмотрим систему (2.3). Назовем главным определителем этой системы определитель 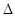 , элементами которого являются коэффициенты при неизвестных:
, элементами которого являются коэффициенты при неизвестных:
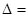
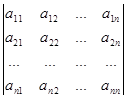 .
.
Предположим сначала, что 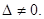 Умножим каждое уравнение системы (2.3) на алгебраические дополнения
Умножим каждое уравнение системы (2.3) на алгебраические дополнения 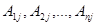 элементов j-го столбца
элементов j-го столбца 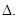
Сложив затем все уравнения, получим:
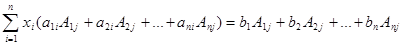 . (2.5)
. (2.5)
Отметим, что 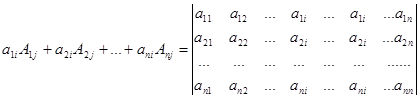 .
.
(j-й столбец)
(Результат получен из разложения определителя по j-му столбцу). Такой определитель равен 0 при 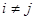 и равен
и равен 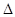 при i = j . Правая часть равенства (2.5) представляет собой определитель
при i = j . Правая часть равенства (2.5) представляет собой определитель 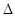 , в котором вместо j-го столбца стоит столбец свободных членов системы (2.3). Назовем такой определитель
, в котором вместо j-го столбца стоит столбец свободных членов системы (2.3). Назовем такой определитель 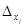 . Рассматривая j = 1,2,…, n, получим систему, эквивалентную исходной:
. Рассматривая j = 1,2,…, n, получим систему, эквивалентную исходной: 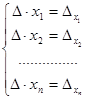 (2.6) . Разделив все уравнения на
(2.6) . Разделив все уравнения на 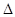 , найдем единственное решение:
, найдем единственное решение: 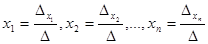 .
.
Предположим теперь, что 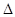 =0. Тогда система (2.6) примет вид:
=0. Тогда система (2.6) примет вид: 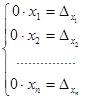 .
.
В этом случае, если все 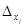 =0, система выглядит так:
=0, система выглядит так: 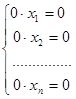 и имеет бесконечно много решений. Если же хотя бы один из
и имеет бесконечно много решений. Если же хотя бы один из 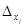
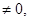 система решений не имеет.
система решений не имеет.
Таким образом, правило Крамера позволяет найти единственное решение системы (2.3) или сделать вывод о существовании бесконечного числа решений либо об их отсутствии:
1) Если 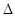
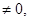 система (2.3) имеет единственное решение, определяемое по формулам:
система (2.3) имеет единственное решение, определяемое по формулам: 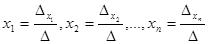 .
.
2) Если 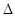 =
= 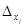 =0, система имеет бесконечно много решений.
=0, система имеет бесконечно много решений.
3) Если 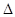 =0, а хотя бы один из
=0, а хотя бы один из 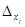
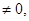 система не имеет решений.
система не имеет решений.
Примеры:
- Рассмотрим систему
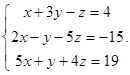 , решенную в предыдущем разделе методом Гаусса, и применим к ней правило Крамера. Найдем все нужные определители:
, решенную в предыдущем разделе методом Гаусса, и применим к ней правило Крамера. Найдем все нужные определители:
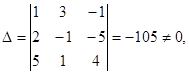 следовательно, система имеет единственное решение.
следовательно, система имеет единственное решение.
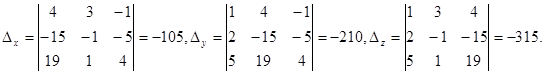
Отсюда 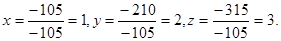
2. 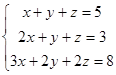 . Здесь
. Здесь 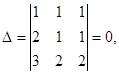 поскольку имеет два одинаковых столбца.
поскольку имеет два одинаковых столбца.
Следовательно, система не имеет единственного решения. Найдем 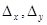 и
и 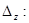
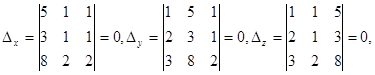 поэтому система имеет бесконечно много решений.
поэтому система имеет бесконечно много решений.
3. 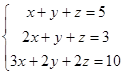 . Для этой системы
. Для этой системы 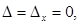 но
но 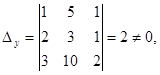
следовательно, решений нет.
Обратная матрица.
Определение 3.7. Квадратная матрица А называется вырожденной, если 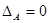 , и невырожденной, если
, и невырожденной, если 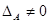 .
.
Определение 3.8. Квадратная матрица В называется обратной к квадратной матрице А того же порядка, если АВ = ВА = Е. При этом В обозначается 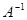 .
.
Рассмотрим условие существования матрицы, обратной к данной, и способ ее вычисления.
Теорема 3.2. Для существования обратной матрицы необходимо и достаточно, чтобы исходная матрица была невырожденной.
Замечание. Сформулируем еще раз способ вычисления обратной матрицы: ее элементами являются алгебраические дополнения к элементам транспонированной матрицы А, деленные на ее определитель.
Пример:
Найдем матрицу, обратную к 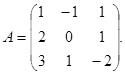
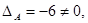 следовательно, матрица А невырожденная. Найдем алгебраические дополнения к ее элементам:
следовательно, матрица А невырожденная. Найдем алгебраические дополнения к ее элементам:
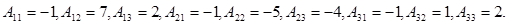 Не забудем, что алгебраические дополнения к элементам строки матрицы А образуют в обратной матрице столбец с тем же номером. Итак,
Не забудем, что алгебраические дополнения к элементам строки матрицы А образуют в обратной матрице столбец с тем же номером. Итак, 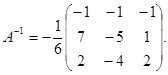 Можно убедиться, что найденная матрица действительно удовлетворяет определению
Можно убедиться, что найденная матрица действительно удовлетворяет определению 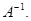 Найдем
Найдем
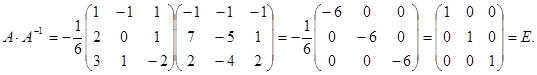
Тот же результат получим и при перемножении в обратном порядке.
Основные теоремы о пределах
1. 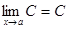
2. 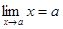
3. 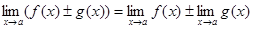
4. 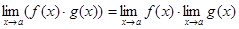
5. 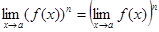
6. 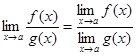
! Все правила имеют смысл, если пределы функций 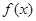 и
и 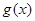 существуют.
существуют.
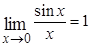 Используются также следующие пределы:
Используются также следующие пределы:
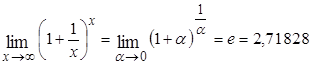
(первый замечательный предел);
(второй замечательный предел).
Техника вычисления пределов
При вычислении предела элементарной функции f(x) приходится сталкиваться с двумя существенно различными типами примеров.
· Функция f ( x ) определена в предельной точке x = a . Тогда
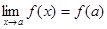 .
.
· Функция f(x) в предельной точке x = a не определена или же вычисляется предел функции при x →∞. Тогда вычисление предела требует в каждом случае индивидуального подхода.
Необходимо помнить, что
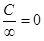 ,
, 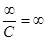 ,
, 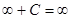 ,
, 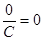 ,
, 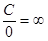 ,
, 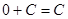 .
. 
Более сложными случаями нахождения предела являются такие, когда функция f(x) в точке x = a или при x→∞ представляет собой неопределенность (типа 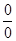 ,
, 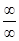 ,
, 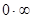 ,
, 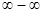 ,
, 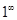 ,
, 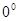 ,
, 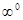 ).
).
При вычислении пределов при 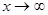 основные теоремы о пределах сохраняют силу и, кроме того, используются правила:
основные теоремы о пределах сохраняют силу и, кроме того, используются правила:
а) чтобы раскрыть неопределенность типа 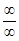 , необходимо числитель и знаменатель дроби разделить на наибольшую степень переменной;
, необходимо числитель и знаменатель дроби разделить на наибольшую степень переменной;
б) чтобы раскрыть неопределенность типа 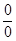 , необходимо числитель и знаменатель дроби разделить на наименьшую степень переменной ;
, необходимо числитель и знаменатель дроби разделить на наименьшую степень переменной ;
в) чтобы раскрыть неопределенность типа 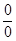 , иногда достаточно числить и знаменатель дроби разложить на множители и затем сократить дробь на множитель, приводящий к неопределенности;
, иногда достаточно числить и знаменатель дроби разложить на множители и затем сократить дробь на множитель, приводящий к неопределенности;
г) чтобы раскрыть неопределенность типа 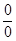 , зависящую от иррациональности, достаточно перевести иррациональность из числителя в знаменатель или из знаменателя в числитель и сократить на множитель, приводящий к неопределенности;
, зависящую от иррациональности, достаточно перевести иррациональность из числителя в знаменатель или из знаменателя в числитель и сократить на множитель, приводящий к неопределенности;
д) чтобы раскрыть неопределенность типа 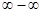 , необходимо числитель и знаменатель дроби одновременно умножить на сопряженное выражение и тем самым свести к неопределенности вида
, необходимо числитель и знаменатель дроби одновременно умножить на сопряженное выражение и тем самым свести к неопределенности вида 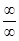 или
или 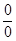 .
.
Вычислить пределы функций:
Пример 1: 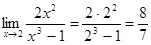
Пример 2: 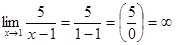
Пример 3: 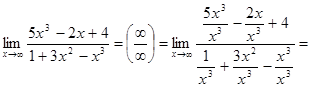
= 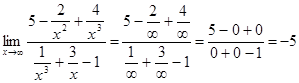
Пример 4: 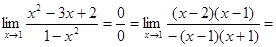
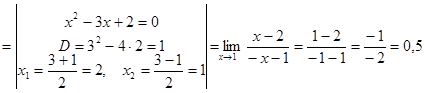
Пример5: 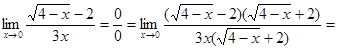
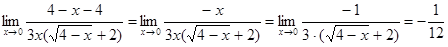
Пример 6:
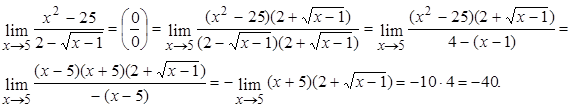
Пример 7:
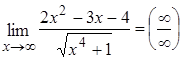 . Теорему о пределе частного здесь применить нельзя, так как числитель и знаменатель дроби конечного предела не имеют. В данном случае имеем неопределённость вида
. Теорему о пределе частного здесь применить нельзя, так как числитель и знаменатель дроби конечного предела не имеют. В данном случае имеем неопределённость вида 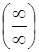 . Разделим числитель и знаменатель дроби на высшую степень х (в данном случае на х2 ), а затем воспользуемся теоремами о пределах функций:
. Разделим числитель и знаменатель дроби на высшую степень х (в данном случае на х2 ), а затем воспользуемся теоремами о пределах функций:
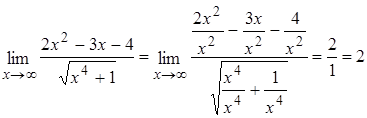 .
.
Здесь мы воспользовались следующим равенством: 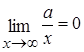 (а – любое число).
(а – любое число).
Пример 8:
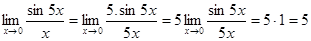
Пример 9:
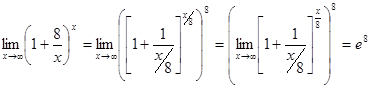
Пример 10:
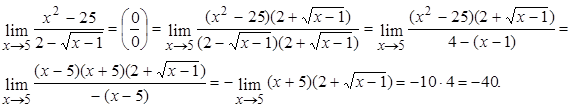
Определение производной
Определение 2.1: Производной функции 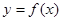 по аргументу x называется предел отношения ее приращения
по аргументу x называется предел отношения ее приращения 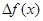 к приращению
к приращению 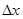 аргумента x, когда приращение аргумента стремится к нулю:
аргумента x, когда приращение аргумента стремится к нулю:
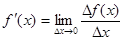 .
.
Если этот предел конечный, то функция y=f(x) называется дифференцируемой в точке x. Если же этот предел есть ∞, то говорят, что функция y=f(x) имеет в точке x бесконечную производную.
Механический смысл производной: скорость есть первая производная пути по времени, т.е. 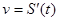 .
.
Геометрический смысл производной: тангенс угла наклона касательной к графику функции 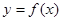 равен первой производной этой функции , вычисленной в точке касания, т.е.
равен первой производной этой функции , вычисленной в точке касания, т.е. 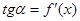
Уравнение касательной к графику функции 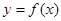 в точке
в точке 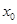 :
:
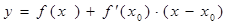
Уравнение нормали к графику функции 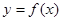 в точке
в точке 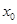 :
:
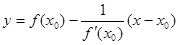
Таблица производных
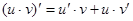
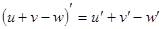
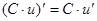
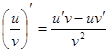
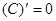
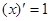
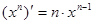
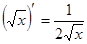
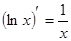
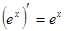
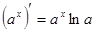
| 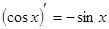
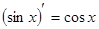
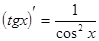
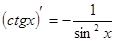
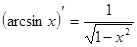
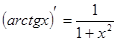
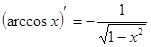
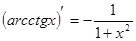
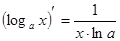
|
Процесс нахождения производных называется дифференцированием функции.
Найти производные функций:
Пример 1: 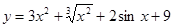
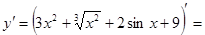
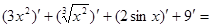
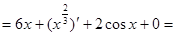
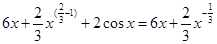 +
+
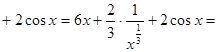
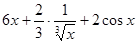
Пример2: 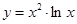
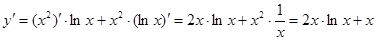
Пример 3: 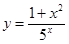
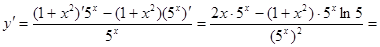
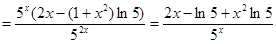
Производные высших порядков
Определение2.2: Производная второго порядка (вторая производная) от функции y=f(x) есть производная от ее первой производной: 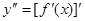 .
.
Определение 2.3 : Производная третьего порядка (третья производная) от функции y=f(x) есть производная от ее второй производной: 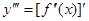 .
.
Определение 2.4 : Производная n -ого порядка (n-я производная) от функции y = f ( x ) есть производная от ее (n -1)-й производной: 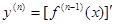 .
.
Рассмотрим примеры.
Пример 1: Найти производную второго порядка 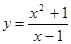 .
.
Решение: 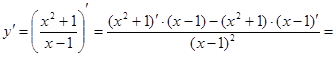
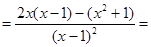
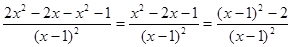
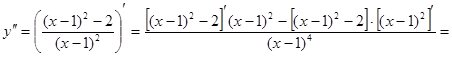
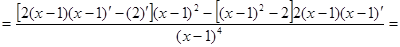
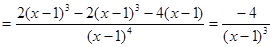
Пример2: Найти производную второго порядка функции 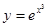 .
.
Решение: 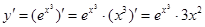
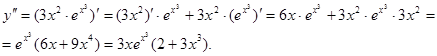
Таблица интегралов
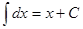
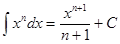
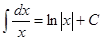
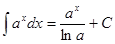
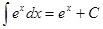
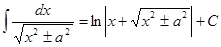
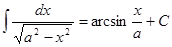
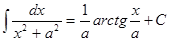 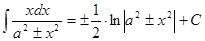
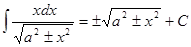
| 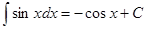
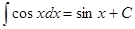
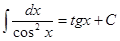
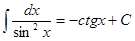
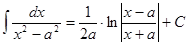
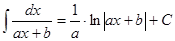
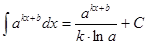
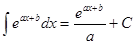 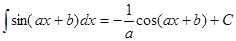 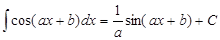
|
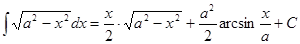
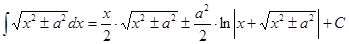
Рассмотрим нахождение интегралов непосредственным методом.
Пример 1: Найти неопределенный интеграл:
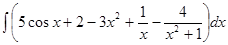 .
.
Решение: 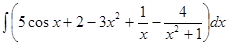 =
=
= 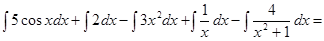
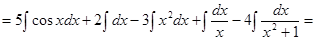

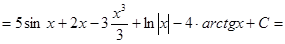
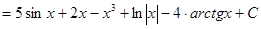 .
.
Пример 2: Найти неопределенный интеграл: 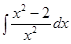 .
.
Решение: 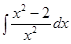 =
= 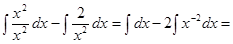

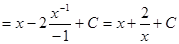 .
.
Пример 3: Найти неопределенный интеграл 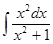
Решение: 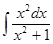 =
= 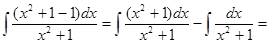
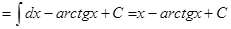
Раздел I Линейная алгебра
Тема 1. Матрицы и определители
Определение 1.1. Матрицей называется прямоугольная таблица чисел.
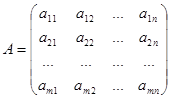
Обозначения: А – матрица, 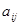 - элемент матрицы,
- элемент матрицы, 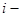 номер строки, в которой стоит данный элемент,
номер строки, в которой стоит данный элемент, 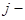 номер соответствующего столбца; m – число строк матрицы, n – число ее столбцов.
номер соответствующего столбца; m – число строк матрицы, n – число ее столбцов.
Определение 1.2. Числа m и n называются размерностями матрицы.
Определение 1.3. Матрица называется квадратной, если m = n. Число n в этом случае называют порядком квадратной матрицы.
Каждой квадратной матрице можно поставить в соответствие число, определяемое единственным образом с использованием всех элементов матрицы. Это число называется определителем.
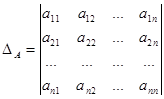
Определение 1.4. Определителем второго порядка называется число, полученное с помощью элементов квадратной матрицы 2-го порядка следующим образом:
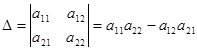 .
.
При этом из произведения элементов, стоящих на так называемой главной диагонали матрицы (идущей из левого верхнего в правый нижний угол) вычитается произведение элементов, находящихся на второй, или побочной, диагонали.
Примеры:
1. 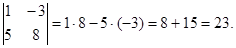 2.
2. 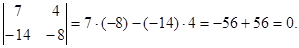
Определение 1.5. Определителем третьего порядка называется число, определяемое с помощью элементов квадратной матрицы 3-го порядка следующим образом:
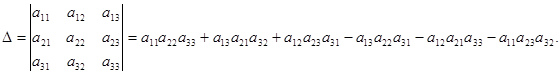
Замечание. Для того, чтобы легче запомнить эту формулу, можно использовать так называемое правило треугольников. Оно заключается в следующем: элементы, произведения которых входят в определитель со знаком «+», располагаются так:















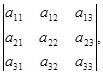 образуя два треугольника, симметричных относительно главной диагонали. Элементы, произведения которых входят в определитель со знаком «-», располагаются аналогичным образом относительно побочной диагонали:
образуя два треугольника, симметричных относительно главной диагонали. Элементы, произведения которых входят в определитель со знаком «-», располагаются аналогичным образом относительно побочной диагонали: 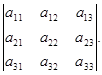
 Примеры.
Примеры.
1. 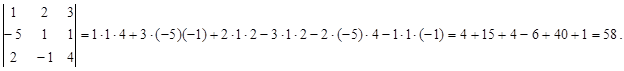
2. 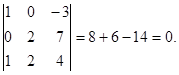
Определение1. 6. Транспонированием матрицы называется операция, в результате которой меняются местами строки и столбцы с сохранением порядка их следования. В результате получается матрица А`, называемая транспонированной по отношению к матрице А, элементы которой связаны с элементами А соотношением a ` ij = aji .
Дата: 2018-12-28, просмотров: 359.