Расчет размерной цепи методом максимума-минимума применяется при индивидуальном и мелкосерийном производстве, проектировании единичных приспособлений. При использовании этого метода исходят из того, что все детали, входящие в сборочную единицу, имеют предельные максимальные или минимальные отклонения от номиналов и сборку производят при самом неблагоприятном сочетании размеров деталей.

Поверочный расчет (задача анализа) линейной размерной цепи методом максимума-минимума состоит в определении номинального и среднего значений размеров замыкающего звена, предельных отклонений и предельной погрешности или допуска размера замыкающего звена.

Номинальное значение размера замыкающего звена

.

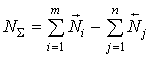
(2.1)

Среднее значение замыкающего звена

.

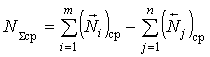
(2.2)

Максимальное (минимальное) значение размера замыкающего звена линейной размерной цепи можно получить, подставив в (4.2) вместо номинальных размеров составляющих звеньев максимальные (минимальные) размеры всех увеличивающих звеньев и минимальные (максимальные) уменьшающих:

,

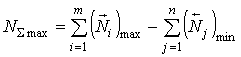(2.3)

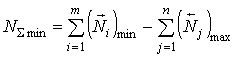
(2.4)

Предельные верхнее (Dв)S и нижнее (Dн)S отклонения размера замыкающего звена от номинального, выраженные через верхние и нижние отклонения размеров составляющих звеньев, определяются как разность предельных размеров замыкающего звена и номинального размера:

,

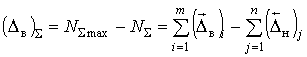(2.5)

.

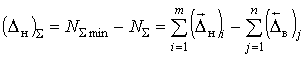(2.6)

Предельная величина погрешности размера замыкающего звена равна разности между его максимальным и минимальным значениями:

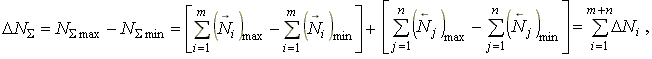
(2.7)

где DNi – погрешности размеров составляющих звеньев.

Заменив в (2.7) погрешности размеров составляющих звеньев допусками на них, можно перейти к уравнению допуска замыкающего звена.

При расчете размерной цепи методом максимума-минимума значение допуска замыкающего звена равно сумме абсолютных значений допусков составляющих звеньев:

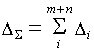
(2.8)

При расчете размерных цепей, как правило, оперируют с половинами полей допусков d и средними значениями отклонений Dср, которые определяются из соотношений:

,

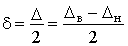(2.9)

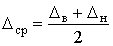
(2.10)

Выражения (2.9) и (2.10) позволяют решить задачу поверочного расчета размерной цепи, когда известными являются не предельные размеры составляющих звеньев, а их предельные отклонения.

В этом случае расчет размерной цепи ведется в следующем порядке.

1. По формулам (2.9) и (2.10) определяются половины полей допусков составляющих звеньев di и средние значения отклонений размеров составляющих звеньев Di ср от номинального.

2. Половина поля допуска размера замыкающего звена из (2.8):

.

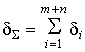3. Среднее значение отклонения размера замыкающего звена от номинального из (2.5) и (2.6) с учетом (2.10)

.

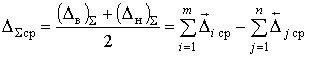(2.12)

4. Допуск размера замыкающего звена

.

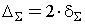5. Предельные отклонения размера замыкающего звена:

, .

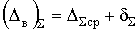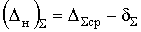6. Размеры замыкающего звена

, .

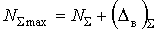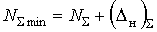Проектный расчет размерных цепей заключается в том, что по заданному номинальному значению замыкающего звена и допуску на него определяют номинальные размеры и рациональные допуски на составляющие звенья.

Решение задачи проектного расчета (синтеза допусков) идет в следующей последовательности.

7.Задаются номинальный NS и предельные NSmax и NSmin размеры замыкающего звена, по которым согласно (4.7) определяют заданную величину поля допуска размера замыкающего звена DS и его половину dS.

8. Заданные значения предельных отклонений из (2.5), (2.6): 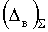 и .

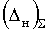9. Заданное значение среднего отклонения размера замыкающего звена 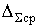 из (2.12).

Заданный допуск замыкающего звена распределяется между составляющими звеньями цепи в соответствии с равенством (2.8).

10. Исходя из полученных допусков на размеры составляющих звеньев и технологии изготовления деталей назначают предельные отклонения размеров составляющих звеньев 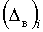и .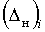

11. Среднее значения отклонений находят из (2.9) и (2.10).

12. По полученным значениям 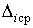 с помощью (2.12) определяют расчетную величину среднего отклонения размера замыкающего звена 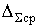, которая сравнивается с заданной 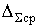. При несовпадении сравниваемых величин в значение вносятся необходимые изменения и производится повторный расчет 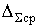. Вычисления продолжаются до равенства расчетной и заданной .

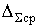Достоинством метода максимума-минимума является его сравнительная простота. Однако если учесть, что в большинстве случаев рассеивание размеров деталей в пределах поля допуска соответствует нормальному закону распределений, то предельные размеры имеют, лишь незначительное количество деталей, и при большом количестве деталей в сборочном соединении вероятность неблагоприятного сочетания размеров весьма мала. Следовательно, применение метода максимума-минимума в известной мере ограничено, так как в большинстве случаев он экономически не оправдан.