Методику моделирования динамики социально-экономических показателей в системе SPSS Base рассмотрим на примере анализа статистических данных по демографической нагрузке в РФ в период 2005-2013 гг. Эмпирической базой анализа служили статистические данные, приведенные в ежегодниках Росстата «Регионы России. Социально-экономические показатели» за 2014, 2010 и 2008 годы (приведены в приложении). Анализу подлежали следующие показатели демографической нагрузки:
- общий коэффициент демографической нагрузки, определяемый как численность лиц нетрудоспособных возрастов в расчете на 1000 человек трудоспособного населения;
- коэффициент демографической нагрузки, определяемый как численность лиц моложе трудоспособного возраста в расчете на 1000 человек трудоспособного населения[1];
- коэффициент демографической нагрузки, определяемый как численность лиц старше трудоспособных возраста в расчете на 1000 человек трудоспособного населения.
Конечной целью анализа является сравнение динамики показателей демографической нагрузки в регионах Центрального федерального округа.
Исходные данные, использованные в примере, приведены в табл. 2)
Таблица 2
Динамика коэффициентов демографической нагрузки в РФ в период 2005-2013 гг. (на 1000 человек трудоспособного возраста)
| Год | 2005 | 2005 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 |
| Всего населения нетрудоспособного возраста | 580 | 578 | 582 | 590 | 606 | 626 | 643 | 664 | 687 |
| Моложе трудоспособного возраста | 258 | 252 | 251 | 253 | 259 | 264 | 271 | 280 | 290 |
| Старше трудоспособного возраста | 322 | 326 | 331 | 337 | 347 | 362 | 372 | 384 | 397 |
В редактор данных системы SPSS Base вводим:
- переменную «год»;
- уровни временных рядов коэффициента демографической нагрузки в РФ – переменные «Всего», «Моложе», «Старше».
Результаты ввода данных приведены на рис. 1 (получен с помощью процедуры «Отчеты итогов в колонках» системы SPSS Base).
| Год Всего Моложе Старше ________ ________ ________ ________ 2005 580 258 322 2006 578 252 326 2007 582 251 331 2008 590 253 337 2009 606 259 347 2010 626 264 362 2011 643 271 372 2012 664 280 384 2013 687 290 397 |
| Рис. 1. Временные ряды коэффициентов демографической нагрузки в РФ в редакторе данных системы SPSS Base |
Как видно из рис. 1, уровни временного ряда общего коэффициента демографической нагрузки равны суммам уровней временных рядов коэффициентов демографической нагрузки, определяемых для лиц моложе и старше трудоспособного возраста.
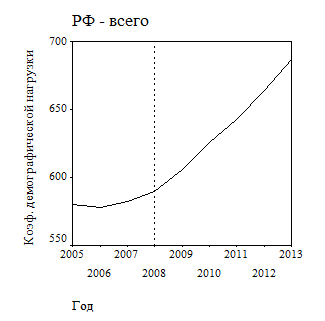
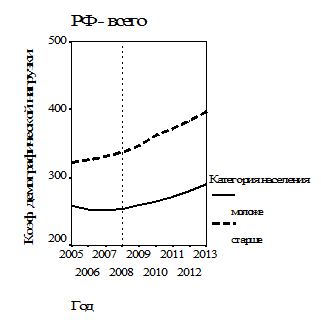
Графики временных рядов коэффициентов демографической нагрузки в РФ, построенные с помощью процедуры «Sequence» (последовательность) системы SPSS Base, представлены на рис. 2.
| а | б |
| 
|
| Рис. 2. Графики временных рядов коэффициента демографической нагрузки в РФ: а – все население нетрудоспособного возраста; б – население моложе и старше трудоспособного возраста. Вертикальной пунктирной линией отмечен 2008 г., отвечающий изменению характера динамики показателей | |
Судя по характеру временных рядов – медленный рост показателей в начале периода наблюдений и ускорение роста после 2008 г. (отмечено вертикальной пунктирной линией), устанавливаем временной диапазон анализа – 2008-2013 гг. и горизонт прогнозирования – 2014-2015 гг.
Поскольку график временного ряда, представленный на рис. 2 а, является суммой временных рядов графиков рис. 2 б, анализ достаточно, в принципе, выполнить только для двух последних показателей – коэффициентов демографической нагрузки населением моложе и старше трудоспособного возраста.
Судя по рис. 2, конкурирующими моделями тренда временных рядов этих показателей могут быть:
1) двухпараметрическая экспоненциальная модель роста вида
х = b0 exp(b1t); (5)
2) трехпараметрическая параболическая модель вида
х = b0 + b1t + b2t2. (6)
Обе модели допускают значение временной переменной t=0, и вместо переменной «год» используем переменную
t=год-2008. (7)
Согласно соотношению (7), начальному году анализируемого периода (2008-му) отвечает значение временной переменной t=0, конечному – 2013-му году – t=5, прогнозным 2014 и 2015 годам – значения временной переменной t=6 и 7 соответственно.
Исходные данные по временным рядам коэффициентов демографической нагрузки в РФ в период 2008-2015 гг., подготовленные к моделированию и прогнозированию, представлены на рис. 3. Расчетные значения уровней временных переменных «Всего», «Моложе», «Старше» пока не определены, а фактические их значения для 2014-2015 гг. на рис. 3 отмечены точками, обозначающими пропуски.
| Год Время Всего Моложе Старше ________ ________ ________ ________ ________ 2008 0 590 253 337 2009 1 606 259 347 2010 2 626 264 362 2011 3 643 271 372 2012 4 664 280 384 2013 5 687 290 397 2014 6 . . . 2015 7 . . . |
| Рис. 3. Исходные данные по временным рядам коэффициентов демографической нагрузки в РФ в период 2008-2015 гг., подготовленные к моделированию и прогнозированию |
Расчет параметров конкурирующих моделей тренда временного ряда проводим в программной среде модуля Curve Estimation пакета SPSS Base.
Результатом моделирования являются:
1) текстовая таблица «ANOVA table», содержащая следующие результаты моделирования:
- статистические характеристики качества модели;
- собственно таблица дисперсионного анализа;
- МНК-оценки параметров модели и их статистические характеристики;
2) графики, отражающие результаты моделирования.
На рис. 4 приведена таблица «ANOVA table» для экспоненциальной модели роста общего коэффициента демографической нагрузки в РФ в период 2008-2013 гг.
Поясним эту таблицу. В ее верхней части приведены статистические характеристики качества модели:
- «Multiple R» – множественный коэффициент корреляции;
- «R Square» – коэффициент детерминации R2;
- «Adjusted R Square» – коэффициент детерминации, скорректированный на число параметров модели;
- «Standard Error» – стандартная ошибка аппроксимации.
В центре таблицы «ANOVA table» – собственно таблица дисперсионного анализа. Приведены для регрессии (Regression) и остатков (Residuals):
- «DF» – число степеней свободы;
- «Sum of Squares» – сумма квадратов;
- «Mean Square» – средний квадрат,
а также критерий Фишера (F) и уровень его статистической значимости (Signif F).
Заключают таблицу «ANOVA table» данные по оценке коэффициентов регрессии (B):
- «ВРЕМЯ» – коэффициент регрессии при временной переменной;
- «(Constant)» – свободный коэффициент модели.
Здесь же приведены:
- ошибки коэффициентов регрессии (SE B);
- величина бета-коэффициента (Beta);
- значения критерия Стьюдента (T);
- уровни их статистической значимости (Sig T).
| MODEL: MOD_4. Dependent variable.. РФ Method.. EXPONENT Listwise Deletion of Missing Data Multiple R ,99927 R Square ,99855 Adjusted R Square ,99818 Standard Error ,00242 Analysis of Variance: DF Sum of Squares Mean Square Regression 1 ,01611387 ,01611387 Residuals 4 ,00002345 ,00000586 F = 2748,13326 Signif F = ,0000 -------------------- Variables in the Equation -------------------- Variable B SE B Beta T Sig T ВРЕ_2008 ,030345 ,000579 ,999273 52,423 ,0000 (Constant) 588,743698 1,031796 570,601 ,0000 |
| Рис. 4. Пример таблицы «ANOVA table» (аппроксимация динамики общего коэффициента демографической нагрузки в РФ в период 2008-2013 гг. экспоненциальной моделью) |
Прокомментируем данные таблицы «ANOVA table». Согласно этим данным, экспоненциальная модель тренда динамики общего коэффициента демографической нагрузки в РФ в период 2008-2013 гг. объясняет 99,9% общей дисперсии при стандартной ошибке аппроксимации логарифма показателя StErr – 0,0024, чему соответствует относительная ошибка аппроксимации показателя 0,24%.
Модель статистически значима на высоком уровне – критерий Фишера F=2748,1, а р-уровень не хуже 0,00005. Это означает, что ошибка признать модель незначимой очень мала – не более 0,005%.
В математической форме модель записывается так:
х = 588,7 exp(0,0303t), (8)
где t – временная переменная, определяемая соотношением
t = год – 2008.
Коэффициент регрессии b1 при временной переменной t (b1=0,0303) статистически значим на высоком уровне – критерий Стьюдента t=52,4 значительно больше критического значения (tкрит@2), и его р-уровень не хуже 0,00005.
Экспоненциальная модель обладает тем положительным свойством, что оба ее параметра имеют четкий смысл:
- коэффициент регрессии при временной переменной t (0,0303) – это МНК-оценка темпа прироста общего коэффициента демографической нагрузки в РФ, которая составляет в среднем 3,03% в год;
- свободный коэффициент b0=588,7 – это расчетная величина общего коэффициента демографической нагрузки в РФ храсч при t=0, т.е. в начальный год временного интервала анализа – 2008 год. Это расчетное значение показателя в 2008 г. достаточно близко к фактическому значению 590.
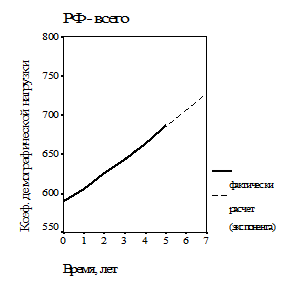
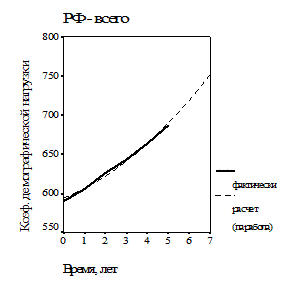
Результаты моделирования в графическом виде для обеих конкурирующих моделей – экспоненциальной и параболической – представлены на рис. 5.
| а | б |
| 
|
| Рис. 5. Моделирование динамики общего коэффициента демографической нагрузки в РФ в 2008-2013 г.: а – экспонентой; б – квадратичным полиномом (параболой). Полужирные линии – фактические временные ряды; пунктирные линии – расчет | |
Параметры и характеристики качества обеих моделей динамики общего коэффициента демографической нагрузки в РФ в 2008-2013 г. приведены в табл. 3
Таблица 3
Параметры и характеристики качества конкурирующих моделей динамики общего коэффициента демографической нагрузки в РФ в 2008-2013 г.
| Модель | Параметр модели | Характеристика качества модели | ||||||
| b0 | b1 | b2 | R2 | F | p | StErr | ||
| 1 | Экспоненциальная | 588,7437 | 0,0303 | - | 0,9986 | 2748,1 | <0,00005 | 0,0024 |
| 2 | Квадратичный полином (парабола) | 590,0357 | 15,8321 | 0,6964 | 0,9994 | 2679,8 | <0,00005 | 1,1052 |
Из табл. 3 следует, что высокими характеристиками качества обладают обе конкурирующие модели динамики общего коэффициента демографической нагрузки в РФ в 2008-2013 г. – каждая из них объясняет более 99% общей дисперсии, обе статистически значимы на высоком уровне (р-уровень не хуже 0,005%).
По коэффициенту детерминации R2 предпочтительнее модель (2) – квадратичная парабола, а по критерию Фишера более предпочтительной является модель (1) – экспонента. Экспоненциальная модель (1) более простая – имеет два параметра, тогда как модель (2) – три. Кроме того, следует учитывать, что полиномы могут быть использованы для интерполяции, но не рекомендуются для использования в прогнозных целях – при экстраполяции за пределы временного диапазона анализа они часто искажают характер тренда, хотя в данном конкретном случае искажения не наблюдается.
Исходя из сравнительного анализа, в качестве модели динамики общего коэффициента демографической нагрузки в РФ в 2008-2013 г. принимаем экспоненциальную модель (1). Дополнительным доводом в ее пользу является четкая интерпретируемость параметров экспоненциальной модели – параметр b0 (свободный коэффициент) равен расчетному значению показателя в начальный год временного диапазона анализа (2008 г.), параметр b1 (коэффициент регрессии при временной переменной) – это среднее значение коэффициента прироста. Коэффициент прироста b1=0,0303, т.е. темп прироста общего коэффициента демографической нагрузки в РФ в 2008-2013 г. в среднем составляет 3,03% в год. Заметим также, что расчетное значение общего коэффициента демографической нагрузки в РФ в 2008 г. храсч(2008)=b0=588,7 достаточно близко к фактическому значению 590.
Ниже в табл. 4 и 5 представлены параметры и характеристики качества экспоненциальных и параболических моделей динамики двух частных коэффициентов демографической нагрузки в РФ в 2008-2013 г. – для лиц моложе и старше трудоспособного возраста.
Таблица 4
Параметры и характеристики качества конкурирующих моделей динамики частного коэффициента демографической нагрузки в РФ в 2008-2013 г. (лица моложе трудоспособного возраста)
| Модель | Параметр модели | Характеристика качества модели | ||||||
| b0 | b1 | b2 | R2 | F | p | StErr | ||
| 1 | Экспоненциальная | 251,6830 | 0,0269 | - | 0,9872 | 307,5 | 0,0001 | 0,0064 |
| 2 | Квадратичный полином (парабола) | 253,4286 | 4,0714 | 0,6429 | 0,9988 | 1239,5 | <0,00005 | 0,6172 |
Таблица 5
Параметры и характеристики качества конкурирующих моделей динамики частного коэффициента демографической нагрузки в РФ в 2008-2013 г. (лица старше трудоспособного возраста)
| Модель | Параметр модели | Характеристика качества модели | ||||||
| b0 | b1 | b2 | R2 | F | p | StErr | ||
| 1 | Экспоненциальная | 337,0544 | 0,0329 | - | 0,9975 | 1574,8 | <0,00005 | 0,0035 |
| 2 | Квадратичный полином (парабола) | 336,6071 | 11,7607 | 0,0536 | 0,9979 | 706,2 | 0,0001 | 1,3390 |
Из табл. 4 и 5 следует, что и экспоненциальные, и параболические модели динамики обеих частных коэффициентов демографической нагрузки в РФ в 2008-2013 г. (для населения моложе и старше трудоспособного возраста) обладают достаточно высокими характеристиками качества и удовлетворяют предъявляемым к аппроксимирующим моделям требованиям. Можно также отметить и близость расчетных значений частных коэффициентов демографической нагрузки в РФ по обеим моделям: для лиц моложе трудоспособного возраста это 251,7 и 253,4 соответственно при фактическом уровне показателя 253 человека на 1000 человек трудоспособного населения в 2008 году, для лиц старше трудоспособного возраста – 337,1 и 336,6 соответственно при фактическом уровне показателя 337 человека на 1000 человек трудоспособного населения.
В то же время, экспоненциальные модели предоставляют аналитику более полную информацию – по величине коэффициента регрессии при временной переменной можно судить о темпах роста демографической нагрузки на трудоспособное население: для лиц моложе трудоспособного возраста средний темп прироста показателя составляет 2,69% в год, для лиц, старше трудоспособного возраста – 3,29% в год. Напомним, что темп прироста общего коэффициента демографической нагрузки в РФ в 2008-2013 г. в среднем составляет 3,03% в год, т.е. демографическую нагрузку на трудоспособное население в большей мере определяется старшим поколением, и это тенденция сохраняется.
Дата: 2018-11-18, просмотров: 706.