ЭЛЕМЕНТЫ ТРЕХФАЗНОЙ СИСТЕМЫ

В настоящее время получение, передача и распределение электроэнергии в большинстве случаев производится посредством трехфазной системы.

Эта система была изобретена и практически разработана во всех основных се частях выдающимся русским инженером М. О. Доливо-Добровольским.

Как показывает само название, трехфазная система состоит из трех источников электроэнергии и трех цепей, соединенных общими проводами линии передачи.

Источником энергии для всех фаз системы является трехфазный генератор (рис. 3.1). Он отличается от однофазного генератора переменного тока тем, что у него на статоре размещены три изолированные друг от друга одинаковые обмотки. Они расположены так, чтобы индуктируемые в них э.д.с. были сдвинуты по фазе одна относительно другой на 120°.

Если генератор двухполюсный, как на рис. 3.1, то оси катушек обмоток фазы сдвинуты одна по отношению к другой на одну треть окружности статора.

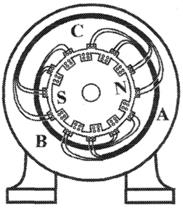
Рис.3.1 Схема устройства трехфазного генератора.

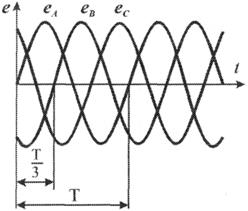
Рис.3.2 Кривые мгновенных значений э.д.с. трехфазной системы.

При вращении ротора его постоянное магнитное поле пересекает проводники обмоток не одновременно. Э.д.с. обмотки А достигает своего максимального значения, когда мимо нее проходит середина полюса ротора. Э.д.с. в следующей обмотке В достигает максимума позже, когда ротор повернется на 1/3 оборота. В двухполюсном генераторе повороту на 1/3 оборота соответствует 1/3 периода индуктируемой э.д.с. Следовательно, э.д.с. в обмотке В отстает по фазе от э.д.с. в обмотке А на 1/3 периода. В свою очередь, э.д.с. в обмотке С отстает по фазе от э.д.с. обмотки Д на 1/3 периода и от э.д.с. обмотки А на 2/3 периода. При такой симметрии устройства генератора максимальные значения этих э.д.с. одинаковы. Конструкция генератора должна обеспечивать их синусоидальность.

Уравнения мгновенных значений э.д.с. будут:

E_A = E_m sin w t                                            

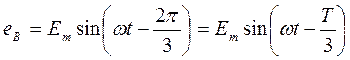                   (3.1)

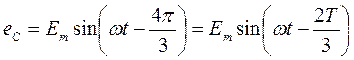
Кривые мгновенных значении э.д.с. показаны на рис. 3.2. На рис. 3.3 дана векторная диаграмма для их действующих значений

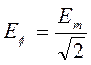
Сумма этих векторов образует замкнутый треугольник: Е_А + Е_В + Е_С = О — это трехфазная симметричная система э.д.с. Алгебраическая сумма мгновенных значений э.д.с. e_А + е _B + е _C = 0, что легко проверить, подставив выражения этих значений как синусоидальных функций времени.

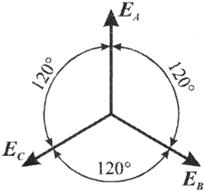
Рис. 3.3 Векторы э.д.с. трехфазной системы.

Изображения э.д.с. трехфазной системы в комплексной форме будут:

Ė _A = E_ф · e^j0 = E_ф                                    

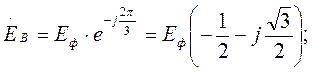                 (3-2)

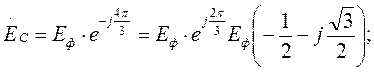
От последовательности фаз системы зависит направление вращения трехфазных двигателей, поэтому в трехфазных устройствах она проверяется специальными указателями последовательности фаз и обозначается раскраской шин на распределительных устройствах; приняты следующие цвета: фаза А — желтый, фаза В — зеленый и фаза С — красный; незаземленная нейтраль — белый, заземленная нейтраль — черный. Зажимы обмоток генератора различают: начала A, В, С, концы X, Y, Z.

Два основных способа соединения обмоток генераторов, трансформаторов и приемников в трехфазных цепях: звездой и треугольником.

СОЕДИНЕНИЕ ФАЗ ЗВЕЗДОЙ

Обмотки фаз генераторов можно было бы соединить с тремя приемниками электроэнергии шестью проводами (рис. 3.4а) и получить таким путем три независимые фазные цепи. Практически подобное соединение применяется лишь в редких случаях, но с помощью такой схемы можно нагляднее представить условия, возникающие при объединении цепей в трехфазную систему. Как и в однофазных цепях переменного тока, стрелки на схеме показывают положительные направления фазных э.д.с. и создаваемых ими токов. Положительные направления определяет разметка зажимов обмоток фаз генератора. Внутри обмоток э.д.с. и токи направлены от «концов» (X, Y, Z) к «началам» (А, В, С). Во внешней цепи токи направлены от начал обмоток фаз генераторов к приемникам.

Для соединения звездой (условное обозначение Y) зажимы X, Y, Z («концы» обмоток фаз генератора) объединяются в одну общую точку N. Соответственно в точке п объединяются и три конца фазных цепей приемника (рис. 3.4б) Между нейтральными точками генератора и приемника проложен общий нейтральный провод (или нейтраль) трехфазной системы, образуемый объединением трех обратных проводов.

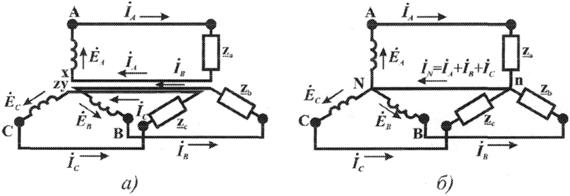
 Рис.3.4 Образование соединения фаз звездой:

а — схема не объединенной трехфазной системы.

б — объединенная трехфазная система

Если предположить равными нулю поочередно все фазные эдс, кроме одной (например, проследить в объединенной системе контур тока IA при наличии в системе одной э.д.с. Е_А) то легко убедиться, что объединение системы не изменит контуры, по которым замыкаются фазные токи. Следовательно, в нейтральном проводе системы ток будет равен векторной сумме фазных токов:

İ _N = İ _A + İ _B + İ _C                                           (3.3)

Нагрузка всех трех фаз называется симметричной, если ток во всех фазах одинаков и равны сдвиги фаз между фазными напряжениями и токами, а также полные сопротивления отдельных фаз приемника (т, е. равны комплексные сопротивления фаз приемника).

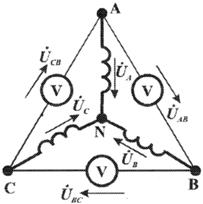
Рис. 3.5. Положительные направления фазных напряжений при соединении фаз звездой.

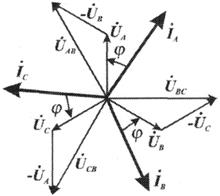
Рис. 3.6. Векторная диаграмма линейных и фазных напряжений

для соединения фаз звездой.

При симметричной нагрузке сумма векторов фазных токов образует замкнутый треугольник. Следовательно, в этом случае ток в нейтральном проводе İ _N = 0. По этой причине для заведомо симметричной трехфазной нагрузки нейтральный провод не нужен. В частности, он не используется для трехфазных двигателей.

При соединении звездой фаз генератора и приемника напряжения на их зажимах называются фазными напряжениями U_ф (U_A , U_B, U _C на рис. 3.5). Но в системе имеются также напряжения между линейными проводами, называемые линейными напряжениями Uл (U_AB,U_BC, U_CA) Положительные направления фазных напряжений противоположны по отношению к приемнику, включенному между линейными проводами (рис. 3.5). Следовательно, каждое из трех линейных напряжений равно векторной разности соответствующих фазных напряжений:

Ů _AB = Ů _A – Ů _B;  

Ů _BC = Ů _B – Ů _C;        (3.4)

Ů_CA = Ů_C – Ů_A;          

Численные соотношения между линейными и фазными напряжениями в симметричной системе легко определить на основании векторной диаграммы (рис. 3.6). За основу диаграммы можно взять три вектора фазных напряжений Ů_A, Ů_B и Ů _C. Углы между ними равны 120 ^o . Для построения вектора линейного напряжения Ů _AB следует из Ů_A вычесть Ů_B, следовательно, нужно к Ů _A прибавить (—Ů_B).

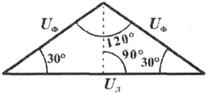
Рис. 3.7. Соотношения между фазными и линейными напряжениями при соединении фаз звездой.

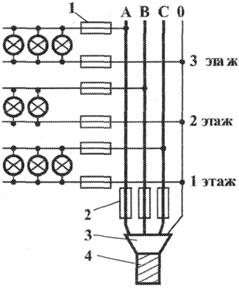
Рис. 3.8. Осветительная нагрузка при соединении приемников

звездой с нейтральным проводом (четырехпроводная система)

1 - квартирные предохранители;

2 - домовые предохранители;

3 - муфта; 4 - кабель.

Последний равен Ů_B по величине, но противоположен ему по направлению. Так же строятся Ů_{B C} и Ů _CA. Так как рассматриваемая система напряжений симметрична, то векторы фазных и линейных напряжений образуют три равнобедренных треугольника с острыми углами по 30° и тупым углом 120°. Опустив из вершины тупого угла любого из треугольников перпендикуляр на противоположную сторону (рис. 3.7), можно найти, что

U_ф cos 30 ^o = U_л /2 или U_л = √3 U_ф;                               

В трехфазной системе, соединенной звездой, линейные напряжения больше фазных в √3 раз. При смешанной осветительной и силовой нагрузке линейное напряжение 380 В подается на зажимы трехфазных двигателей, а фазное 220 В=380/ √3 — на осветительные приборы.

При соединении звездой токи в проводах линии передачи—линейные токи I_Л равны фазным, так как все части фазной цепи и линейные провода соединены последовательно: I_Л = I_Ф.

При осветительной нагрузке в случае соединения звездой приемники включаются между линейными проводами и нейтральным проводом.

Часто осветительная нагрузка бывает несимметричной, в этом случае необходим нейтральный провод (рис. 3.8). При отсутствии нейтрального провода в зависимости от отношения сопротивлений фаз приемника одно фазное напряжение может быть ниже необходимого, а другое слишком велико. По этой причине в нейтральном проводе магистрали запрещается устанавливать предохранители или выключатели.