1. Переменными э.д.с., напряжениями и токами называют э.д.с., напряжения и токи, периодически изменяющиеся во времени. Для мгновенного значения периодической величины, например, э.д.с., можно записать:
e = f (t + kT)
где Т - период или время полного цикла изменения э.д.с.,
k - целое число.
Мгновенные значения электрических величин в цепях переменного тока обозначают строчными буквами.
2. Среди периодических э.д.с. и токов наибольшее распространение получили синусоидальные э.д.с. и токи. Мгновенное значение синусоидальной величины, например, тока, записывается так:
i = Im sin w t
где Im - амплитудное значение тока,
w - угловая частота,
f- частота изменения тока, связанная с периодом соотношением:
w = 2 p f, f = 1/T
3. Синусоидально изменяющаяся величина характеризуется амплитудой, частотой (или периодом) и начальной фазой. Фазой называется аргумент синуса, фаза определяет состояние синусоидально изменяющейся величины в данный момент времени.
Величину аргумента синуса при t = 0 называют начальной фазой. На графиках начальную фазу отсчитывают от ближайшего к точке с координатой t = 0 перехода синусоидальной функции через ось абсцисс от отрицательных значений к положительным. При таком порядке отсчета положительная начальная фаза направлена в положительную сторону оси абсцисс, а отрицательная - в обратную сторону (рис.2.1б и 2.1 а). Обозначается начальная фаза буквой "кси" - y.
Для синусоидального тока, изображенного на рисунке 2.2 при различных значениях начальной фазы, можно написать следующие выражения мгновенных значений:
для рисунка 2.la
i = Im sin w t
для рисунка 2.1б
i = Im sin ( w t + y I ),
для рисунка 2.1в
i = Im sin ( w t - y I ),
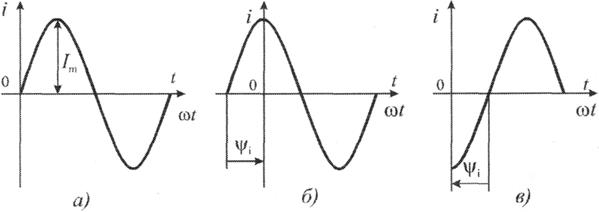
Рис. 2.1. Графики синусоидального тока при различных значениях начальной фазы
4. Если на одном графике изображаются для совместного рассмотрения две синусоидальные функции, то разность их начальных фаз называют углом сдвига фаз или просто сдвигом фаз (j). При сопоставлении напряжений и токов чаще всего определяют сдвиг фаз, вычитая из начальной фазы напряжения начальную фазу тока:
j = y U - y I ,
Определение сдвига фаз поясняется рисунком 2 .
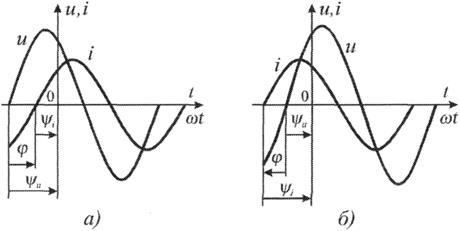
Рис. 2.2. Обозначение сдвига фаз на графиках напряжения и тока
5. Для оценки величин синусоидально изменяющихся тонов, э.д.с. и напряжений нельзя применять их средние значения, так как среднее за период значение любой синусоидальной величены равно нулю. В качестве оценки этих величин вводится так называемое действующее значение тока, э.д.с. или напряжения, например:
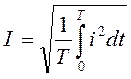
Можно показать, что если переменная величина, в данном случае ток изменяется по синусоидальному закону, то
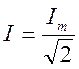 ,
,
то есть действующее значение тока равно максимальному, деленному на корень из двух.
Главное преимущество действующего значения синусоидально изменяющейся величины в том, что оно не зависит от времени, следовательно, его удобно изображать на графиках, с его помощью легко проводить всевозможные расчеты. Большинство электроизмерительных приборов сконструировано так, что они фиксируют именно действующие значения синусоидальных токов и напряжений.
6. Синусоидальные токи, э.д.с. и напряжения можно изображать векторами. Это значительно проще, чем изображение с помощью синусоид. Совокупность векторов, изображающих синусоидально изменяющиеся с одинаковой частотой токи, напряжения и э.д.с. и представленных в определенном порядке, называют векторной диаграммой.
Ток и напряжение, представленные на рисунках 2.1, 2.2 в виде синусоид, изображены на рисунке 2.3 с помощью векторов.
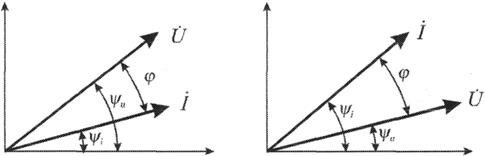
Рис. 2.3. Векторные диаграммы токов и напряжений.
При построении векторных диаграмм положительные углы отсчитываются по направлению против часовой стрелки.
7. Индуктивные катушки и конденсаторы оказывают сопротивление протекающим по ним переменным токам. В этих сопротивлениях не происходит превращения электрической энергии в тепловую. Поэтому в отличие от активных сопротивлений их называют реактивными. Реактивное сопротивление индуктивной катушки называется индуктивным сопротивлением, обозначается XL, и вычисляется по формуле:
XL = w L, Ом
где L - индуктивность катушки, Г (генри).
Реактивное сопротивление конденсатора называется емкостным сопротивлением, обозначается ХС и вычисляется по формуле:
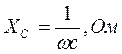
где С - емкость конденсатора в фарадах.
8. Известно, что в активном сопротивлении напряжение совпадает с током по фазе. Если ток, текущий по сопротивлению на рисунке 2.4а задан выражением
i = Im sin w t
то напряжение на этом сопротивлении изменяется по закону:
u = Um sin w t
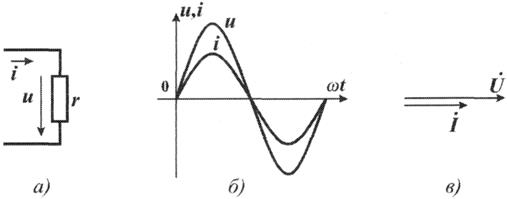
Рис. 2.4 Ток и напряжение в активном сопротивлении.
Синусоиды тока и напряжения, а также их векторная диаграмма представлена на рис.2.4 б, в.
В катушке индуктивности напряжение опережает ток по фазе на угол 90o . Если ток катушки задан выражением:
i = Im sin w t
то напряжение на катушке изменяется по закону:
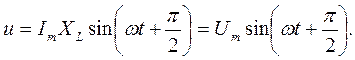
Схема цепи, синусоиды тока и напряжения, также их векторная диаграмма приведены на рисунке 2.5.
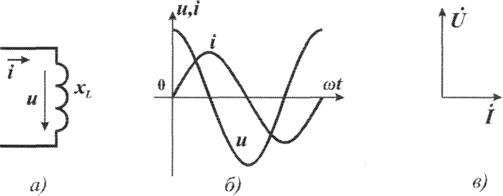
Рис. 2.5 Ток и. напряжение в катушке индуктивности.
В конденсаторе напряжение отстает от тока по фазе на угол 90°. Если ток, протекающий через конденсатор, задан выражением:
i = Im sin w t
то напряжение на конденсаторе изменяется по закону:
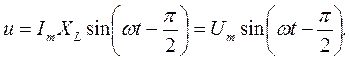
Схема цепи, синусоиды тока и напряжения, а также их векторная диаграмма приведены на рисунке 2.6.
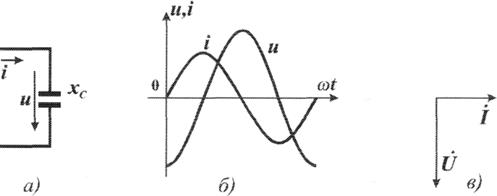
Рис.2.6 Ток и напряжение конденсатора
9. Так как в цепях переменного тока с активными и реактивными элементами токи и напряжения сдвинуты друг относительно друга по фазе, то активные и реактивные сопротивления и проводимости можно складывать только квадратично.
При последовательном соединении элементов (рисунок 2.7а) полное сопротивление цепи определяется по формуле:
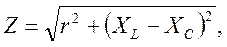
при параллельном соединении элементов (рисунок 2.7б) полная проводимость цепи определяется по формуле:
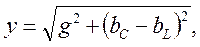
где g, b - соответственно активная и реактивная проводимость цепи.
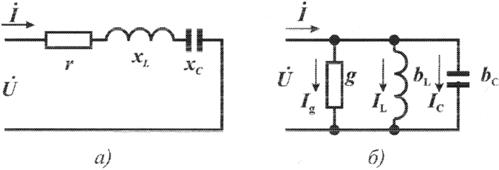
Рис.2.7 Электрическая цепь с последовательным и параллельным соединением элементов.
10. Пусть необходимо построить векторные диаграммы токов и напряжений для схем, представленных на рисунке 2.7.
На схеме рис. 2.7а все сопротивления соединены последовательно, поэтому за основу для построения векторной .диаграммы можно принять ток, являющийся общим элементом для сопротивлений. В произвольном направлении в определенном масштабе откладывают вектор тока I (рисунок 2.8а). Известно, что вектор напряжения на активном сопротивлении совпадает с током по фазе, поэтому откладывают в выбранном масштабе вектор U r совпадающим по направлению с током.
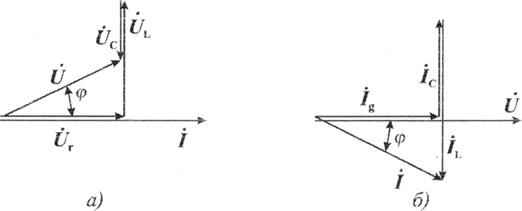
Рис. 2,8 Векторные диаграммы электрических цепей
Так как индуктивное напряжение опережает ток по фазе на угол 90°, то из конца вектора Ur, откладывают вектор UL выбранном масштабе и повернутым относительно тока на угол p/2 против часовой стрелки. Tак как емкостное напряжение Uc отстает по фазе от тока на угол 90°, то из конца вектора UL откладывают вектор Uc. В выбранном масштабе и повернутым относительно тока на угол p/2 по часовой стрелке.
Так как напряжение на входе схемы Ů согласно второго закона Кирхгофа не может быть ничем иным, как суммой падений напряжении в цепи, то
U = Ur + UL + UC
Поэтому вектор, соединяющий начало U r и конец, Uc есть вектор сетевого напряжения U.
Векторная диаграмма для цепи по рисунку 2.8б строится точно так же, но так как все элементы схемы соединены параллельно, то начинают построение с единого для всех сопротивлений элемента - напряжения U.
Угол сдвига по фазе j (фи) между током и напряжением находят из треугольника сопротивлений или треугольника проводимостей.

Например, для схемы на рисунке 2.7 тангенс угла сдвига по фазе между сетевым напряжением и током равен:
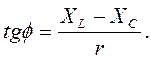
II. Пример .
Дана схема, изображенная на рисунке 2.9. Напряжение на зажимах цепи изменяется по закону:
U = 10 sin w t
Даны параметры: R1, = 5 Ом, R2 = 7 Ом, L = 0,1 Г, С = 135 мк Ф, f= 40 Гц.
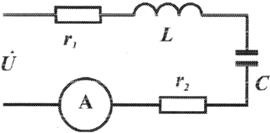
Рис 29 Схема для расчет» цепи
Определить: показание амперметра, закон изменения тока в цепи, построить векторную диаграмму.
11.1. Определяют реактивные сопротивления. Индуктивное сопротивление:
XL = w t.
XL = 2 p f L = 2 p × 40 × 0,1 = 25,1 Ом
Емкостное сопротивление:
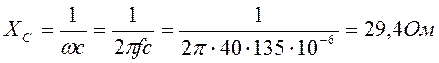
11.2. Так как все элементы цепи на рисунке 2.9 соединены последовательно, то по ним протекает один и тот же ток. Определяют его по закону Ома как частное от деления напряжения на зажимах цепи на полное сопротивление цепи.
11.2.1. Амперметр показывает действующее значение тока, поэтому необходимо воспользоваться действующим значением приложенного напряжения:
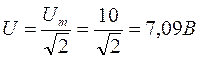
11.2.2. Полное сопротивление цепи определяют исходя из следующих соображений.
Напряжения на активных сопротивлениях цепи совпадает по фазе, следовательно, активное напряжение цепи
Ur = Ur1 + Ur2,
откуда, разделив правую и левую части равенства на ток, получают
r = r1 + r2.
Напряжения на катушке индуктивности и конденсаторе противоположны по фазе, следовательно, реактивное напряжение цепи
Up = UL – UC,
откуда, разделив правую и левую части равенства на ток, получают
X = XL – XC = w L – 1/ w c.
Известно, что активное и реактивное сопротивление цепи с последовательным соединением параметров складываются квадратично, следовательно, полное сопротивление электрической цепи находят по выражению:
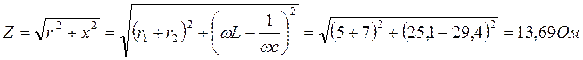
11.2.3. Показание амперметра:
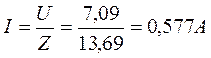
11.3. Прежде, чем написать закон изменения тока в цепи, можно построить векторную диаграмму, из которой можно определить, опережает или отстает ток по фазе от приложенного напряжения.
На векторной диаграмме должны быть представлены в векторной форме все токи и напряжения, реально существующие в цепи. Из рисунка 2.9 видно, что по всем элементам цепи протекает один и тот же ток. На всех сопротивлениях он вызывает падения напряжений, сумма которых равна сетевому напряжению (согласно второму закону Кирхгофа).
Как правило, векторная диаграмма отроится для действующих значений токов и напряжений. Ток рассчитан в п. 11.2.3. Определим величины падений напряжений на сопротивлениях:
Ur1 = I × r1 = 0,58 × 5 = 2,9 B
Выбирают масштабы для тока и напряжения. Пусть, например, в 1 см. содержится 0,1 А, и в 1 см, - 2 В. Построение векторной диаграммы для цепи с последовательным соединением элементов удобнее начать с вектора тока. От произвольной точки плоскости в произвольном направлении откладывают вектор тока I (рисунок 2.10)
Напряжение на активном сопротивлении r1 совпадает по фазе с током, поэтому вектор U r совпадает по направлению с вектором тока I.
Напряжение на катушке UL, опережает ток по фазе на 90° . Из конца вектора Url откладывают вектор UL под углом 90°, причем, угол отсчитывают от вектора тока против часовой стрелки.
Напряжение на конденсаторе отстает от тока по фазе на угол девяносто градусов. Поэтому от конца вектора U I. откладывают вектор Uc под углом 90° по отношению к вектору тока, причем, угол отсчитывается по часовой стрелки.
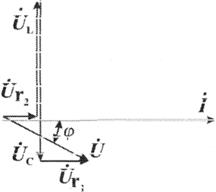
Рис. 2.10. Векторные диаграммы при последовательном и параллельном соединении параметров цепи
Напряжение на сопротивлении r2 совпадает с током по фазе. Поэтому от конца вектора UL откладывают вектор U I параллельно вектору тока. Направления векторов Ur2 и I должны совпадать.
Так как по второму закону Кирхгофа можно записать:
U = Ur1 + UL + UC + Ur2
то, соединяя начало вектора Ur1 с концом вектора Ur2 , получают вектор сетевого напряжения U. Из рисунка 2.10 видно, что вектор сетевого напряжения отстает по фазе от вектора тока, следовательно, полное сопротивление цепи носит активно-емкостный характер.
11.4. Известно, что в линейных электрические цепях ток изменяется по синусоидальному закону, если по этому же закону изменяется питающее напряжение.
По условию
U = Um sin w t
Вектор тока опережает вектор сетевого напряжения на угол j, следовательно, закон изменения тока в цепи по рисунку 2.10 можно написать так:
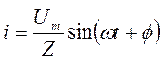
Определим численное значение угла j:
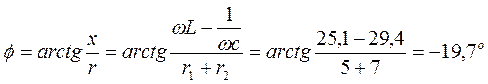
«Минус» свидетельствует о том, что вектор напряжения является отстающим по фазе. Это равнозначно утверждению: вектор тока является опережающим по фазе. Поэтому в формулу закона изменения тока величина угла войдет со знаком «плюс».
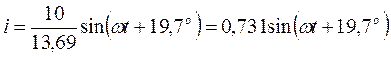
Дата: 2018-11-18, просмотров: 923.