Результаты экспериментов обычно представляют не только в виде таблиц, но и в графической форме. Для графиков следует использовать специальную бумагу (миллиметровую, логарифмическую или полулогарифмическую). При построении графиков следует разумно выбирать масштабы, чтобы измеренные точки располагались на всей площади, листа. Графическое представление результатов позволяет быстро понять основные характерные черты наблюдаемой зависимости и обнаружить ошибочные результаты.
Точки, наносимые на графики, должны изображаться четко и ясно. Их следует отмечать карандашом, так как иначе ошибочно нанесенную точку нельзя удалить с графика, не испортив его. Способ изображения на графике экспериментальных результатов зависит от того, известна ли их погрешность. Если она неизвестна (что чаще всего и бывает), то результаты изображаются точками, а если известна, то лучше изображать их не точками, а крестами. Полуразмер креста по горизонтали должен быть равен стандартной погрешности по оси абсцисс, а его вертикальный полуразмер – погрешности по оси ординат. Оси графика должны иметь ясные, четкие обозначения. Рядом с делениями – на удобных расстояниях – должны быть нанесены цифры, позволяющие установить значения, соответствующие делениям шкалы. Цифры принято располагать по краям сетки.
Через экспериментальные точки всегда следует проводить самую, простую кривую, совместимую с этими точками, т. е. кривую, от которой экспериментальные данные отступают, как правило (в 2/3 случаев), не более чем на стандартную ошибку. При проведении кривой нужно следить за тем, чтобы на каждом достаточно большом ее участке экспериментальные точки располагались как выше, так и ниже кривой. При графической обработке результатов следует помнить, что на глаз можно точно провести через экспериментальные точки только прямую линию. Поэтому при построении графика следует стремиться к тому, чтобы ожидаемая зависимость имела вид прямой линии.
Задача о проведении наилучшей прямой сводится в этом случае к подбору параметра в формуле
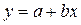(7)
Приведем правила для определения погрешностей, которые следует приписывать графически найденным параметрам прямой линии. Пусть прямая описывается формулой (7).
Чтобы найти погрешность в определении параметра а, нужно смещать прямую вниз параллельно самой себе, пока выше нее не окажется вдвое больше точек, чем снизу.(Нижняя пунктирная линия на рисунке 6) Затем следует сместить ее вверх, пока снизу не окажется вдвое больше точек, чем сверху.
 |
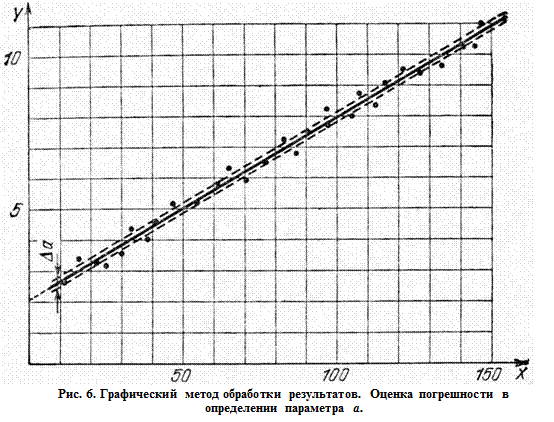(Верхняя пунктирная линия на рис.6)
Наилучшей прямой будет средняя прямая, между проведенными по правилам.
Пусть смещение между этими прямыми равно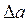 
(см. рис. 6). Погрешность в определении величины 
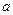равна
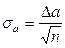(8)
где п – полное число точек на графике.
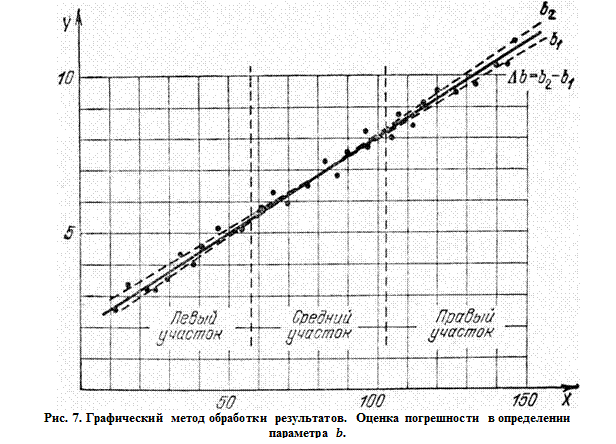
Погрешность в определении параметра b находится аналогичным образом (рис. 7). «Рабочий участок» оси абсцисс (участок, на котором расположены экспериментальные точки) делится на три равные части. Средний участок в дальнейшей работе не участвует. Для определения σb прямая поворачивается так, чтобы на левом участке выше нее оказалось вдвое больше точек, чем под ней, а на правом участке – наоборот. Затем кривая поворачивается так, чтобы на левом участке 2/3 точек лежали ниже прямой, а на правом – выше нее. Обозначим разницу в угловых коэффициентах этих прямых через Δb. Тогда
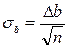, (9)
где п – полное число точек на графике.
В качестве наилучшей прямой будет средняя прямая (проведенная как биссектриса).
Если экспериментальная прямая точно проходит через начало координат и может быть задана формулой
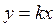(10)
«Рабочим» участком в этом случае является весь диапазон по оси X от нуля до последней точки.Его следует разбить на три части и самую левую – ближнюю к началу координат – часть во внимание не принимать. Затем нужно провести через начало координат две прямые так, чтобы выше одной из них лежало 2/3 точек, а выше другой – 1/3. Различие между этими прямыми определяет Δk. Стандартная погрешность находится по формуле
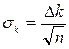, (11)
где п – полное число точек на графике.
1.9. Методика определение параметров наилучшей прямой
аналитическим методом
Параметры наилучшей прямой можно определить не только графически, но и аналитически. Приведем соответствующие формулы. Пусть при значениях х i одной физической величины получены значения у i для другой величины (i=1, 2, ..., п). Наилучшая прямая (7) определяется по правилу «наименьших квадратов», т. е. параметрам а и b приписываются такие значения, при которых величина
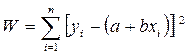(12)
имеет минимум. При этом получаются следующие формулы для нахождения наилучших значений а и b по измеренным: значениям х i, у i (i = 1, 2,..., п):
, 
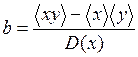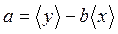, (13)
где
, 
, 
,
, 
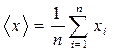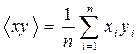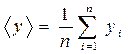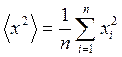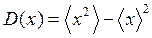(14)
При расчетах следует помнить, что в числителе первой формулы обычно вычитаются близкие по величине члены, что вызывает необходимость удерживать при вычислениях много значащих цифр.
Приведем формулу для определения параметра k: прямой (10), проходящей через начало координат:
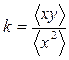. (15)
Укажем, наконец, формулы для оценки погрешностей параметров а, b и k:
, 
, 
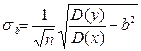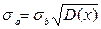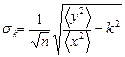, (16)
Входящая в формулы (16) дисперсия D(x) определяется по формуле (14). Аналогичным образом вычисляется и D(y),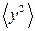 
.
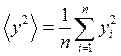
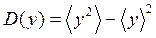(17)
Вычисления удобно проводить, используя таблицы Exel.
2. Практическая часть:
I. Определение ускорения свободного падения с помощью маятника.
1. Ознакомьтесь с экспериментальной установкой (рис. 6) и правилами работы с секундомером.
2. Определите время своей реакции. Для этого быстро включите и выключите секундомер. Полученное значение используйте в качестве систематической погрешности измерения времени.
3. 
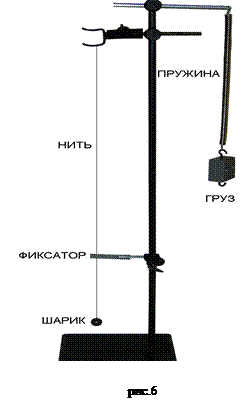
С помощью штангенциркуля измерьте диаметр шарика, закрепленного на нити. Запишите полученную величину и систематическую погрешность измерения.
4. Установите расстояние от шарика до отверстия фиксатора l1=10см. Для измерений используйте металлическую линейку.
5. Вызовите колебания маятника небольшой амплитуды (1 – 2 см).
6. С помощью секундомера измерьте время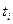 
, в течение которого маятник совершает N=40 полных колебаний. Данные занесите в таблицу 1.
7. Проделайте 20 измерений, в каждом новом опыте увеличивая длину нити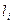 
на 2-3см.
8. Результаты измерений длины маятника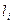 
и времени 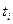за которое он совершает N=40 полных колебаний занесите в таблицу 1
9. По формуле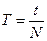 
вычислите периоды колебани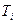й 
и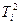 
для каждого значения 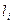и занесите результат в таблицу 1.
Таблица 1.
| № п/п | li, мм | N | ti, c | Ti, c | Ti2, c2 |
| 1. | |||||
| 2. | |||||
| … | |||||
| 20. |
4. По данным таблицы 1 постройте график зависимости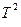 
от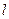 
. Для этого нанесите точки на график 
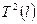и проведите через них наилучшую прямую, в соответствии с п.п. 1.8 методических указаний.
5. Продолжите прямую до пересечения с осью ОХ. Найдите значение l 0 и оцените его погрешность (см. п.п. 1.8 методических указаний).
6. Сравните значение l 0 с радиусом шарика. Сделайте вывод о том, до какой точки надо измерять длину нити, чтобы прямая проходила через начало отсчета.
7. Определите угловой коэффициент наклона прямой к оси ОХ: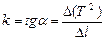 
.
8. Найдите ускорение свободного падения g: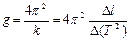 
.
9. Рассчитайте стандартную погрешность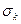 
при определении параметра 
: 
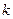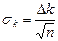, где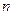 
- полное число точек на графике. ( См. п.п. 1.8 методических указаний).
10. Рассчитайте погрешность измерения g: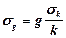 
.
11. Окончательный результат представьте в виде: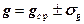 
.
12. Сделайте вывод, сравните с теоретическим значением.
II. Исследование зависимости периода колебаний маятника от угла отклонения.
1. Установите лапку штатива так, чтобы шарик находился на высоте 0,5-1,0 см над подставкой штатива. На подставку положите линейку, шарик должен находился над ее серединой.
2. Установите длину нити от шарика до отверстия фиксатора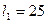 
см.
3. Отклоните маятник на небольшой угол 2-40 . Отклонение (амплитуду)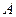 
измерьте по линейке. Отпустите шарик. С помощью секундомера измерьте время 
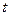, за которое маятник совершает 
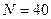полных колебаний. Найдите период колебаний. Данные занесите в таблицу 2.
Таблица 2.
| № п/п | l, мм | А, мм | N | t, c | T, c |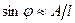 
| j |
| 1. | |||||||
| 2. | |||||||
| 3. | |||||||
| 4. | |||||||
| 5. | |||||||
| 6. | |||||||
| 1. | |||||||
| 2. | |||||||
| 3. | |||||||
| 4. | |||||||
| 5. | |||||||
| 6. |
4. Повторите опыт из п.3 5-6 раз, причем, при каждом следующем измерении увеличивайте амплитуду колебаний маятника, вплоть до амплитуды, соответствующей углу отклонения примерно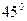 
. Результаты опытов занесите в таблицу 2.
5. Изменяя высоту фиксатора над подставкой штатива, измените длину нити маятника. Для новой длины нити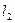 
маятника проделайте задания 3-4.
6. По данным таблицы (для каждой длины нити отдельно) постройте два графика зависимости периода колебаний маятника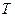 
от начального угла отклонения 
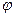. По виду графика сделайте вывод о зависимости 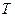от .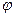
7. Определите, в каком диапазоне значений угла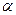 
следует проводить измерения периода колебаний маятника, чтобы не учитывать зависимость 
.
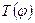8. Запишите вывод.
3. Контрольные вопросы.
1. Что такое колебания?
2. Приведите пример колебательных процессов.
3. Какие колебания называются периодическими?
4. Что такое период колебаний, в каких единицах измеряется период колебаний?
5. Что такое частота колебаний, в каких единицах измеряется частота в системе СИ?
6. Что такое амплитуда, колебаний, в каких единицах измеряется амплитуда колебаний?
7. Какие колебания называются гармоническими?
8. Запишите формулу для периода гармонических колебаний, поясните величины, входящие в неё.
9. Что такое циклическая частота? Запишите формулу связи между циклической частотой и частотой?
10. Что такое фаза колебаний, начальная фаза колебаний?
11. Какое уравнение называют дифференциальным уравнением гармонических колебаний?
12. Как связаны между собой при колебаниях координата, скорость, ускорение?
13. Какие колебания называются свободными?
14. Какие колебания называются незатухающими, а какие затухающими?
15. Какие колебания называются вынужденными?
16. Что такое резонанс? При каких условиях он наступает?
17. Какую систему называют маятником?
18. Что такое математический маятник?
19. Чему равна циклическая частота колебаний математического маятника?
20. Чему равен период колебаний математического маятника?
21. С какой частотой происходят колебания кинетической энергии маятника?
22. Для одного из опытов рассчитайте натяжение нити в крайней точке и при прохождении положения равновесия.
23. Изменится ли период колебаний, если на нить той же длины повесить больший шарик?
24. Какое допущение в теории приводит к тому, что период колебаний маятника не должен зависеть от амплитуды колебаний?
25. Как должен влиять момент инерции шарика на период колебаний?
4. Рекомендуемая литература.
1. Сивухин Д. В. Общий курс физики. Т. I. Механика.- М.: Наука, 1979.
2. Стрелков С. П. Механика.- М.: Наука, 1975, 560 с.
3. Методическое пособие по обработке результатов измерений, Мн., МГЭУ, 2005, 36 с.
5. Литература, использованная при подготовке пособия.
1. Физика: задание № 4 для 11-х классов (2002-2003 учебный год). Сост.: В.И.Чивилев, - М.: МФТИ, 2002, 32 с.
2. Стрелков С. П. Механика.- М.: Наука, 1975, 560 с.
3. Элементарный учебник физики: Учебное пособие. т.3/ под ред. Г.С.Ландсберга,-М.: «Шрайк», 1995 – 608 с.
4. Лабораторный практикум по общей физике: Учебное пособие. т.1/ А.Д.Гладун, Д.А.Александров, Ф.Ф.Игошин и др., под ред. А.Д.Гладуна. -М.: МФТИ, 2004 – 316 с.
5. Физическая энциклопедия / Гл. ред. А. М. Прохоров. Ред. кол. Д. М. Алексеев, А. М. Балдин, А. М. Бонч-Бруевнч, А. С. Боровик-Романов и др.- М.: Сов. энциклопедия. Т. 1. Аронова – Бома эффект – Длинные линии. 1988. 704 с, ил.
Дата: 2018-11-18, просмотров: 643.
