Лабораторная работа № 6
ИЗУЧЕНИЕ ГАРМОНИЧЕСКИХ КОЛЕБАНИЙ
МАТЕМАТИЧЕСКОГО МАЯТНИКА
Минск
2013
ИЗУЧЕНИЕ ГАРМОНИЧЕСКИХ КОЛЕБАНИЙ
МАТЕМАТИЧЕСКОГО МАЯТНИКА
Цель работы: определить зависимость периода колебаний маятника от угла начального отклонения нити; пользуясь маятником, определить величину ускорения свободного падения.
Приборы и оборудование: стальной шарик на нити, штатив, фиксатор нити, секундомер, штангенциркуль, металлическая линейка.
Теоретическая часть
Колебания
Колебаниями называются процессы, в той или иной степени повторяющиеся во времени.
Если мы говорим, что система колеблется, то под этим подразумевается, что некоторая физическая величина, характеризующая систему, совершает колебания, т. е. изменяется, неоднократно принимая одно и то же значение.
Свободные и собственные колебания. Затухание.
Свободными колебаниями (или собственными) называются колебания, происходящие в системе, предоставленной самой себе в отсутствие внешних воздействий. Такие колебания возникают в системе в результате однократного выведения ее из состояния устойчивого равновесия. При свободных колебаниях в системе всегда действуют силы (в общем случае причины), стремящиеся возвратить систему в положение равновесия (положение, при котором в системе отсутствуют колебания). В случае колебаний груза на пружине возвращающей силой будет сила упругости пружины. Частота, с которой происходят собственные колебания, называется собственной частотой колебаний.
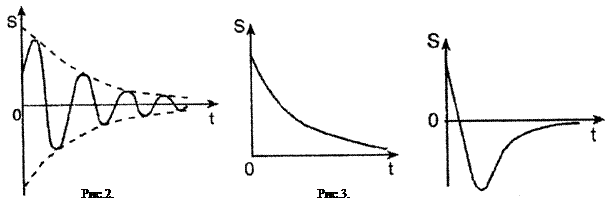
Колебания, которые происходят с постоянным размахом (амплитудой) колеблющейся величины в течение всего времени наблюдения, называют незатухающими. Колебания, идущие с постоянно уменьшающимся размахом, называют затухающими.
Свободные колебания реальных систем всегда затухающие. Механические колебания затухают, главным образом, из-за трения и возбуждения в окружающей среде упругих волн. В электрических колебательных системах затухание вызывается тепловыми потерями в проводниках, потерями энергии на излучение электромагнитных волн. Чем сильнее препятствующее колебаниям воздействие, тем быстрее затухают колебания и прекращаются вовсе.
Наличие трения или любого другого сопротивления колебаниям вызывает торможение колебательного процесса, что приводит к увеличению периода, точнее, условного периода. Дело в том, что при затухании те понятия периода и частоты, которые были введены нами ранее, теряют смысл, т. к. затухающие колебания идут с уменьшающимся размахом колеблющейся физической величины, и нет строгой повторяемости значений у колеблющейся величины.
Следует отметить, что небольшое затухание слабо меняет период. Например, если амплитуда колебаний уменьшается за период приблизительно в 1,5 раза, то периоды, рассчитанные без учета затухания и по более точной формуле, учитывающей затухание, будут отличаться всего на 0,2 %. Даже когда амплитуда колебаний уменьшается в 3–7 раз за период (сильное затухание), погрешность в определении периода по формуле, не учитывающей затухание, составит не более 5 %.
К сказанному выше о затухающих колебаниях можно добавить, что при увеличении затухания в системе условный период возрастает и при некоторых условиях обращается в бесконечность. Это означат, что изменение величины S не носит колебательного характера, а представляет собой так называемый апериодический процесс. На рис. 2 приведен пример зависимости S ( t ) для затухающего колебания, а примеры апериодических процессов даны на рис. 3 и 4. Значение S при t = 0, т. е. начало графика S ( t ), для затухающих колебаний или апериодического процесса зависит от того, в каком положении была система в момент начала наблюдений.
Периодические колебания
Колебания некоторой физической величины S называются периодическими, если все значения этой величины полностью повторяются через одно и то же время Τ , называемое периодом, т. е. S ( t + Τ) = S ( t ) для любого значения времени t . Если Τ – период, то 2Т, 3Т , 4Τ ,... тоже периоды. Поэтому в физике под периодом обычно понимают наименьший период, т. е. наименьший отрезок времени, через который физическая величина S повторяется. При этом говорят, что за время одного периода совершается одно колебание.
Частотой периодических колебаний ν называется число колебаний в единицу времени. Легко показать, что
.
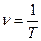Действительно, если за время t совершено N колебаний, то частота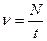 
, а период 
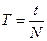. Отсюда видно, что 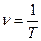. В системе СИ единицей измерения частоты служит Герц (Гц), 1 Гц = с-1.
Пусть периодически колеблющаяся величина S изменяется в пределах от S0 – А до S0 + А, где А > 0. Тогда говорят, что величина S колеблется с амплитудой А около значения S 0 . Размах колебаний (разница между двумя крайними положениями) равен 2А.
Гармонические колебания
Важным частным случаем периодических колебаний являются гармонические колебания, т. е. такие изменения во времени t физической величины S , которые идут по закону
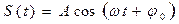, (1)
где А > 0, ω > 0. Из курса математики известно, что функция вида (1) меняется в пределах от – А до А , и что наименьший положительный период у нее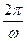 
. Поэтому гармоническое колебание вида (1) происходит с амплитудой А и периодом 
.
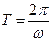Не следует путать циклическую (круговую) частоту ω и частоту ν колебаний.
Между ними простая связь. Так как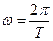 
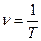и , то
.
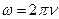В системе СИ размерность как ω, так и ν равна с-1. Наименование Гц обычно применяется только для величины ν , а если необходимо указать размерность ω, то пишут просто с-1.
Величина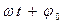 
называется фазой колебаний. Фаза растет пропорционально времени. При t = 0 фаза равна 
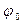, и поэтому 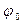называется начальной фазой. Она зависит от отклонения и скорости в момент начала отсчета времени.
Отметим, что при одном и том же t: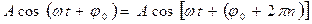 
, где n=0, ±1, ±2, … Видно, что начальная фаза для одного и того же колебания есть величина, определенная с точностью до 2π n . Поэтому из множества возможных значений начальной фазы выбирают, обычно, модуль ее наименьшего значения.
Иногда полезно знать характер изменения первой и второй производных по времени от величины S , которая совершает гармонические колебания (колебания по гармоническому закону). Если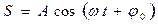 
, то дифференцирование S по времени t дает
, 
.
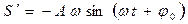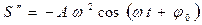С учетом (1) получаем, что 
, т.е.
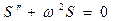. (2)
Равенство (2) называют дифференциальным уравнением гармонических колебаний.
Таким образом, мы получили чрезвычайно важное утверждение:
если используя законы физики для физической величины S удалось записать дифференциальное уравнение вида 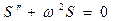, то отсюда будет следовать, что S изменяется обязательно, по гармоническому закону 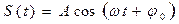с циклической частотой 
( 
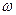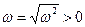). Конкретные значения амплитуды А и начальной фазы 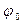зависят от начальных условий.
Заметим, что в (2) стоит величина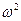 
, которая всегда положительна. Поэтому, например, уравнение 
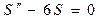не будет дифференциальным уравнением гармонических колебаний, т.к. не найдется такого действительного значения 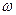, для которого 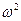было бы равно « – 6 ».
Лабораторная работа № 6
ИЗУЧЕНИЕ ГАРМОНИЧЕСКИХ КОЛЕБАНИЙ
МАТЕМАТИЧЕСКОГО МАЯТНИКА
Минск
2013
Дата: 2018-11-18, просмотров: 565.
