Колебательная система не всегда бывает предоставлена самой себе, совершая при этом свободные (в общем случае затухающие) колебания. На колебательную систему может действовать внешнее периодическое возмущающее воздействие, под влиянием которого в системе возникают так называемые вынужденные колебания.

Вынужденными колебаниями называют колебания системы, вызванные действием на нее внешней периодической силы (внешнее периодическое воздействие), называемое вынуждающей силой. Если подвешенный на пружине груз двигать рукой вверх-вниз с некоторой частотой, то роль вынуждающей силы выполняет сила, действующая на груз со стороны руки.

Интересно, что при некотором значении (или даже значениях) частоты внешнего воздействия, называемой резонансной частотой, наступает резонанс – резкое возрастание амплитуды установившихся вынужденных колебаний. Резонанс наступает при частоте внешнего воздействия, близкой к собственной.

Если же вынужденные колебания происходят под действием периодической с частотой ν, но не гармонической силы, а собственные колебания системы гармонические, то резонанс наступает тогда, когда какое-либо значение из набора ν, 2ν, 3ν, ... совпадает с частотой собственных колебаний (на практике из-за наличия затухания это совпадение только приближенное). Например, математический маятник (или качели) можно сильно раскачивать, если сильно толкать его (действовать с периодической, но не гармонической силой) не только с частотой, равной собственной, но и с частотой в целое число раз меньше собственной, т. е. толкать один раз за период колебаний, один раз за два периода, один раз за три периода и т. д.

В наиболее общем случае вынужденных колебаний, происходящих под действием периодической, но не гармонической силы частоты ν и когда собственные колебания частоты ν_с тоже не гармонические, резонанс наступает, если какое-нибудь число из набора ν, 2ν, 3ν, 4ν,... будет близко к какому-либо числу из набора ν_с, 2ν_с, 3ν_с, ... Резонанс при этом может проявляться как сильно, так и слабо. Все зависит от характера собственных колебаний и характера внешнего периодического воздействия.

Периодические колебания

Колебания некоторой физической величины S называются периодическими, если все значения этой величины полностью повторяются через одно и то же время Τ , называемое периодом, т. е. S ( t + Τ) = S ( t ) для любого значения времени t . Если Τ – период, то 2Т, 3Т , 4Τ ,... тоже периоды. Поэтому в физике под периодом обычно понимают наименьший период, т. е. наименьший отрезок времени, через который физическая величина S повторяется. При этом говорят, что за время одного периода совершается одно колебание.

Частотой периодических колебаний ν называется число колебаний в единицу времени. Легко показать, что

.

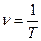Действительно, если за время t совершено N колебаний, то частота 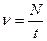, а период 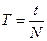. Отсюда видно, что 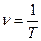. В системе СИ единицей измерения частоты служит Герц (Гц), 1 Гц = с^-1.

Пусть периодически колеблющаяся величина S изменяется в пределах от S₀ – А до S₀ + А, где А > 0. Тогда говорят, что величина S колеблется с амплитудой А около значения S ₀ . Размах колебаний (разница между двумя крайними положениями) равен 2А.

Гармонические колебания

Важным частным случаем периодических колебаний являются гармонические колебания, т. е. такие изменения во времени t физической величины S , которые идут по закону

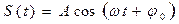,                                           (1)

где А > 0, ω > 0. Из курса математики известно, что функция вида (1) меняется в пределах от – А до А , и что наименьший положительный период у нее 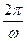. Поэтому гармоническое колебание вида (1) происходит с амплитудой А и периодом .

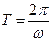Не следует путать циклическую (круговую) частоту ω и частоту ν колебаний.

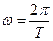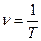Между ними простая связь. Так как  и , то

.

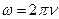В системе СИ размерность как ω, так и ν равна с^-1. Наименование Гц обычно применяется только для величины ν , а если необходимо указать размерность ω, то пишут просто с^-1.

Величина 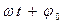 называется фазой колебаний. Фаза растет пропорционально времени. При t = 0 фаза равна 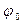, и поэтому  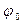называется начальной фазой. Она зависит от отклонения и скорости в момент начала отсчета времени.

Отметим, что при одном и том же t: 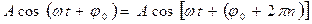, где n=0, ±1, ±2, … Видно, что начальная фаза для одного и того же колебания есть величина, определенная с точностью до 2π n . Поэтому из множества возможных значений начальной фазы выбирают, обычно, модуль ее наименьшего значения.

Иногда полезно знать характер изменения первой и второй производных по времени от величины S , которая совершает гармонические колебания (колебания по гармоническому закону). Если 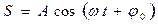, то дифференцирование S по времени t дает

, .

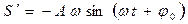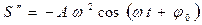 С учетом (1) получаем, что , т.е.

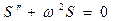.                                                       (2)

Равенство (2) называют дифференциальным уравнением гармонических колебаний.

Таким образом, мы получили чрезвычайно важное утверждение:

если используя законы физики для физической величины S удалось записать дифференциальное уравнение вида 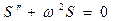, то отсюда будет следовать, что S изменяется обязательно, по гармоническому закону  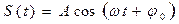с циклической частотой  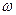( 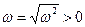). Конкретные значения амплитуды А и начальной фазы  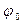зависят от начальных условий.

Заметим, что в (2) стоит величина 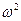, которая всегда положительна. Поэтому, например, уравнение  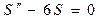не будет дифференциальным уравнением гармонических колебаний, т.к. не найдется такого действительного значения 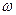, для которого  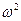было бы равно « – 6 ».