Для того, чтобы некоторую величину можно было обозначать булевой переменной, должны выполняться следующие ограничения:
1. Величина должна принимать два возможных состояния, но не более того.
2. В любой момент времени величина не может принимать оба состояния одновременно.
3. В любой момент времени величина не может принимать ни одного состояния.
4. Если рассматриваются несколько таких величин, то допускается, чтобы каждая из них принимала одно из двух состояний независимо.
5. Не допускается применять одну пару состояний для одной величины, а для другой — другую.
Эти 5 правил определяют ситуации, в которых алгебра логики может быть применена. Рассмотрим пример. Пусть речь идет о цехе автомобильного завода, где сушатся только что покрашенные автомобили, и мы хотим применить алгебру логики, рассуждая об автомобилях в этом цеху.
Мы можем применить алгебру логики к цвету автомобилей, если все они либо "зеленые", либо "красные".
По правилу 1, если в цехе есть помимо красных и зеленых еще и желтые автомобили, то мы не можем применить алгебру логики, деля их на "красные" и "зеленые". Потому, что кроме двух значений "красный" и "зеленый" появляется третье — "желтый". Можно выйти из затруднения, рассмотрев автомобили "зеленые" и "незеленые" (то есть всех остальных цветов).
По правилу 2, если в цехе есть красные автомобили в зеленую полоску или зеленые в красный горошек, то мы не можем применить алгебру логики, деля их на "красные" и "зеленые". Потому, что о некоторых автомобилях можно будет сказать, что он и "красный", и "зеленый" одновременно. Можно выйти из затруднения, если договориться считать "красными" автомобили, которые сначала покрывают красной краской.
По правилу 3, если в цехе есть помимо красных или зеленых вовсе некрашеные автомобили, то мы не можем применить алгебру логики, деля их на "красные" и "зеленые". Потому, что о некрашеных автомобилях еще нельзя сказать, что они красные или зеленые. Можно выйти из этого затруднения, если считать красными те автомобили, которые запланировано покрасить в красный цвет, а зелеными те, которые запланировано покрасить в зеленый.
По правилу 4, если в цехе не все автомобили одновременно зеленые или красные, это не помешает применению алгебры логики к цвету автомобилей. С другой стороны, если в цехе всегда только красные автомобили или только зеленые, то нет смысла заводить столько переменных, сколько автомобилей. Достаточно одной переменной для всех автомобилей сразу.
По правилу 5, если в цехе есть только зеленые и красные автомобили, и все они — либо сломаны, либо исправны, то мы все равно не можем смешивать в одних и тех же формулах переменные, обозначающие цвет автомобилей, и их исправность. Из этого затруднения можно выйти, если рассматривать не цвет и исправность самих автомобилей, а истинность или ложность правильно составленных фраз насчет цвета и исправности. Таким образом, каждому автомобилю будет соответствовать две булевы переменные: "автомобиль зеленый" и "автомобиль исправный". Каждая переменная может принимать два значения "истина" или "ложь".
Правила 1, 2, 3 и 5 должны обязательно выполняться все. Если не выполняется хотя бы одно из них, алгебра логики не применима. Правило 4 поясняет одну ситуацию, когда могут возникнуть сомнения насчет применения алгебры логики.
Примеры демонстрируют следующие практические факты. Во-первых, алгебра логики может быть применена не всегда, а лишь с соблюдением определенных ограничений. Во-вторых, если алгебра логики не может быть применена одним способом, то часто можно обнаружить другой способ — совсем рядом. Достаточно немного изменить условия.
В этом нет ничего необычного или сомнительного — так работает вся математика. Нужно просто проявлять с одной стороны внимательность, а с другой — изобретательность. Например, в арифметике нельзя суммировать гайки и яблоки по количеству, но зато их можно суммировать по весу. Эта ситуация очень похожа на ту, когда нельзя применить булеву алгебру к цвету и исправности, но можно применить к фразам о цвете и исправности.
Булева алгебра весьма распространена. Принцип работы большинства компьютеров основан на ней. Большинство формул математики могут быть только истинными или ложными, так что булева алгебра применима и почти ко всей математике. Оказывается, что и в обыденной речи алгебра логики вполне применима, хотя не везде и не всегда. Таким образом, булева алгебра полезна, но не претендует на сверхуниверсальность. Это — инструмент, который может оказаться, удобен для решения определенных задач, для других — неудобен, а для третьих — вообще неприменим.
Логические задачи
Для решения многих логических задач необходимо:
1) выделить элементарные (простые) высказывания и обозначить их буквами;
2) записать условие задачи на языке алгебры логики, соединив простые высказывания в сложные с помощью логических операций;
3) составить единое логическое выражение для всех требований задачи;
4) используя законы алгебры логики попытаться упростить полученное выражение и вычислить все его значения либо построить таблицу истинности для рассматриваемого выражения;
5) выбрать решение — набор значений простых высказываний, при котором логическое выражение является истинным;
6) проверить, удовлетворяет ли полученное решение условию задачи.
Еще один способ решения логических задач заключается в том, чтобы по условию задачи составить таблицу истинности. Анализ полученной таблицы истинности зачастую позволяет получить требуемый результат.
Примеры задач
1. Задача. Компьютер вышел из строя (нет изображения на экране монитора), однако неизвестно какое устройство не работает (монитор, видеокарта или оперативная память). Можно предположить следующее:
1) Если монитор исправен или видеокарта неисправна, то оперативная память неисправна;
2) Если монитор исправен, то оперативная память исправна.
Исправен ли монитор?
Решение
1. Рассмотрим простые высказывания:
А = {Монитор неисправен},
В = { Видеокарта неисправна},
С = { Оперативная память неисправна}.
2. Запишем на языке алгебры логики наши предположения:
( 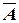 Ú В ) Þ С и
Ú В ) Þ С и 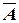 Þ
Þ 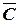 .
.
3. Пусть F ( A , B , C ) = (( 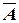 ÚВ) Þ С ) & (
ÚВ) Þ С ) & ( 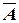 Þ
Þ 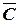 ).
).
4. Составим для данного высказывания таблицу истинности:
| A | B | C | 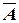
| 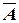 Ú В Ú В
| ( 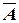 Ú В ) Þ С Ú В ) Þ С
| 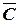
| 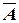 Þ Þ 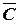
| F |
| 0 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 0 |
| 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 0 |
| 0 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 1 |
5. Решить данную задачу — значит указать, при каких значениях А полученное сложное высказывание истинно. Необходимо проанализировать все строки таблицы истинности, где F = 1. Анализ таблицы показывает, что сложное высказывание истинно во всех случаях, когда А — истинно, т. е. вероятнее всего неисправен именно монитор.
2. Задача: "Финансовый прогноз"
Три подразделения — A, B, C — торговой фирмы стремились получить по итогам года максимальную прибыль. Экономисты высказали следующие предположения:
1. A получит максимальную прибыль только тогда, когда получат максимальную прибыль B и C.
2. Либо A и B, получат максимальную прибыль одновременно, либо одновременно не получат.
3. Для того чтобы С получило максимальную прибыль, необходимо, чтобы и В получило максимальную прибыль.
По завершении года оказалось, что одно из трех предположений ложно. Какие из названных подразделений получили максимальную прибыль?
Решение
Рассмотрим простые высказывания:
А = {А получит максимальную прибыль};
B = {В получит максимальную прибыль};
С = {С получит максимальную прибыль};
Запишем на языке алгебры логики прогнозы, высказанные экономистами:
1) F1 = A  B & C;
B & C;
2) F2 = A & C V A & C;
3) F3 = C  B.
B.
Теперь составим таблицу истинности для F1, F2, F3.
| А | В | С | F1 | F2 | F3 |
| 0 | 0 | 0 | 1 | 1 | 1 |
| 0 | 0 | 1 | 1 | 0 | 0 |
| 0 | 1 | 0 | 1 | 1 | 1 |
| 0 | 1 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 |
Где 0 — "ложь" , 1 — "истина".
Теперь вспомним, что ложным оказался один из прогнозов — F1, F2, F3. Эта ситуация соответствует четвертой строке таблицы.
Ответ: B и С получат максимальную прибыль.
3. Задача. По обвинению в ограблении перед судом предстали Иванов, Петров, Сидоров. Следствие установлено следующее:
1. Если Иванов не виновен или Петров виновен, то Сидоров виновен.
2. Если Иванов не виновен, то Сидоров не виновен.
Виновен ли Иванов?
Решение
Рассмотрим простые высказывания:
A = {Иванов виновен}
B = {Петров виновен}
C = {Сидоров виновен}.
Запишем на языке алгебры логики факты, установленные следствием:
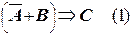
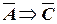

Пусть
Решить задачу – это значит указать, при каких значениях А это сложное высказывание истинно, и если хотя бы в одном случае (при разных B и C) F = 1 A = 0 (Иванов не виновен), то у следствия недостаточно фактов для того, чтобы обвинять Иванова в преступлении.
Таблица истинности
| A | B | C | 
|  Ú В Ú В
| ( 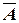 Ú В ) Þ С Ú В ) Þ С
| 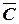
| 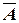 Þ Þ 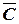
| F |
| 0 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 0 |
| 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 0 |
| 0 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 1 |
Из таблицы истинности видно, что сложное высказывание истинно только когда A — истинно, т.е. Иванов виновен в ограблении.
4. Задача “КОМИССАР МЕГРЭ”
Мегрэ, вернувшись домой, позвонил на набережную Орфевр.
— Говорит Мегрэ. Есть новости?
— Да, шеф. Поступили сообщения от инспекторов. Торранс установил, что если Франсуа был пьян, то либо Этьен убийца, либо Франсуа лжет. Жуссье считает, что или Этьен убийца, или Франсуа не был пьян, и убийство произошло после полуночи. Инспектор Люка просил передать вам, что если убийство произошло после полуночи, то либо Этьен убийца, либо Франсуа лжет. Затем звонила…
— Все. Спасибо. Этого достаточно. — Комиссар положил трубку. Он знал, что трезвый Франсуа никогда не лжет. Теперь он знал все.
Решение
Рассмотрим следующие простые высказывания:
А = {Франсуа был пьян},
В = {Этьен убийца},
С = {Франсуа лжет},
D = {убийство произошло после полуночи}.
Перепишем на языке алгебры логики условие задачи. Инспектора комиссара Мегрэ установили, что
А Þ (В Ú С) = 1,
В Ú (А & D) = 1,
D Þ (В Ú С) = 1.
Сам Мегрэ знает, что
А & С = 1.
Истинной будет и конъюнкция четырех высказываний:
(A Þ (B Ú C) & (B Ú (A & D)) & (D Þ (B Ú C)) & ( A & C).
Ответ: Франсуа был пьян, Этьен убийца, Франсуа лжет, убийство произошло после полуночи.
5. Задача. Виктор, Роман, Леонид и Сергей заняли на математической олимпиаде четыре первых места. Когда их спросили о распределении мест, они дали три таких ответа:
1. Сергей — первый, Роман — второй;
2. Сергей — второй, Виктор — третий;
3. Леонид — второй, Виктор — четвертый.
Известно, что в каждом ответе только одно утверждение истинно.
Как распределились места?
Решение
Рассмотрим простые высказывания:
С1 = (Сергей занял первое место),
Р2 = (Роман занял второе место),
С2 = (Сергей занял второе место),
В3 = (Виктор занял третье),
Л2 = (Леонид занял второе место),
В4 = (Виктор занял четвертое место).
На языке алгебры логики ответы ребят можно записать следующим образом:
С1 Ú Р2 = 1,
С2 Ú В3 = 1,
Л2 Ú В4 = 1.
Конъюнкция истинных высказываний истинна. Следовательно, имеет место равенство:
(С1 Ú Р2) & (С2 Ú В3) & (Л2 Ú В4 ) = 1.
Раскроем скобки:
С1&С2&Л2 Ú C2&Р2&Л2 Ú С1&В3&Л2 Ú Р2&В3&Л2 Ú С1&С2&В4 Ú
0 0 1 0 0
Ú С2&Р2&В4 Ú С1&В3&В4 Ú Р2&В3&В4
0 0 0
Нули в равенстве означают, что получились несовместимые условия, исходя из того, что участник математической олимпиаде не может одновременно занимать несколько мест и каждое место распределяется одному участнику.
Единственное выражение, значение которого может быть истинным это
С1&В3&Л2 = 1.
Другими словами, места на олимпиаде распределились так:
Сергей — 1-е место,
Леонид — 2-е место,
Виктор — 3-е место,
Роман — 4-е место.
6. Задача. Алеша, Боря и Гриша нашли в земле старинный сосуд. Рассматривая удивительную находку, каждый высказал по два предложения:
Алеша: “Это сосуд греческий и изготовлен в V веке”.
Боря: “Это сосуд финикийский и изготовлен в III веке”.
Гриша: “Это сосуд не греческий и изготовлен в IV веке”.
Учитель истории сказал ребятам, что каждый из них прав только в одном из двух предположений.
Где и в каком веке изготовлен сосуд?
Решение
Рассмотрим простые высказывания:
А = (сосуд греческий),
В = (сосуд финикийский),
С = (сосуд изготовлен в III веке),
D = (сосуд изготовлен в IV веке),
Е = (сосуд изготовлен в V веке ).
Запишем предположения школьников на языке алгебры логики.
А Ú Е = 1 (слова Алеша),
В Ú С = 1 (слова Бори),
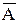 Ú D = 1 (слова Гриши).
Ú D = 1 (слова Гриши).
Если все эти высказывания логически перемножить, то получится истинное сложное высказывание:
( A Ú E ) & (B Ú C) & ( 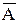 Ú D) = 1
Ú D) = 1
Раскроем скобки:
A&B & 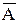 Ú
Ú 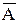 &B&E Ú
&B&E Ú 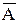 &A&C Ú
&A&C Ú 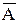 &E&C Ú D&A&B Ú D&B&E
&E&C Ú D&A&B Ú D&B&E
0 1 0 0 0 0
Ú D&A&C Ú D&E&C.
0 0
Исходя из того, что сосуд мог быть изготовлен только в одной стране и в одном веке, нули в равенстве означают, что получились несовместимые условия.
Единственное выражение, значение которого может быть истинным это E&B& 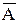 = 1.
= 1.
Мы установили, что сосуд финикийский и изготовлен в V веке, что удовлетворяет условию задачи.
Дата: 2018-11-18, просмотров: 372.