С помощью логических операций над высказываниями из заданной совокупности высказываний можно строить различные сложные высказывания. При этом порядок выполнения операций указывается скобками. Например, из трёх высказываний Х, Y, Z можно построить высказывания
( X & Y ) Ú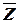 
и X 
.
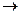
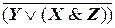Первое из них есть дизъюнкция конъюнкции X, Y и отрицания высказывания Z, а второе высказывание есть импликация, посылкой которой является высказывание X, а заключением – отрицание дизъюнкции высказывания y и конъюнкции высказываний X, Z.
Всякое сложное высказывание, которое может быть получено из элементарных высказываний посредством применения логических операций отрицания, конъюнкции, дизъюнкции, импликации и эквивалентности, называется ФОРМУЛОЙ АЛГЕБРЫ ЛОГИКИ.
Для упрощения записи формул принят ряд соглашений. Скобки можно опускать, придерживаясь следующего порядка действий: конъюнкция выполняется раньше, чем все остальные операции, дизъюнкция выполняется раньше, чем импликация и эквивалентность. Если над формулой стоит знак отрицания, то скобки тоже опускаются.
В связи с этим приведенные выше формулы ( X & Y ) Ú 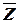и X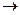 
могут быть написаны так: X & Y Ú 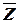и X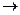 
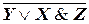, а также XY Ú 
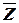и X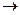 
.
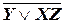Логическое значение формулы алгебры логики полностью определяется логическими значениями входящих в неё элементарных высказываний. Например, логическим значением формулы 
в случае, если Х = 1, Y = 1, Z = 0 будет истина, т.е. = 1.
Как и в случае с логическими операциями все возможные логические значения формулы, в зависимости от значений входящих в неё элементарных высказываний, могут быть описаны полностью с помощью таблицы истинности.
Таблицу, показывающую, какие значения принимает составное высказывание при всех сочетаниях (наборах) значений входящих в него простых высказываний, называют таблицей истинности составного высказывания.
Для любой формулы достаточно просто построить таблицу истинности.
Алгоритм построения таблицы истинности:
1. подсчитать количество переменных n в логическом выражении;
2. определить число строк в таблице m = 2n;
3. подсчитать количество логических операций в формуле;
4. установить последовательность выполнения логических операций с учетом скобок и приоритетов;
5. определить количество столбцов в таблице: число переменных плюс число операций;
6. выписать наборы входных переменных с учетом того, что они представляют собой натуральный ряд n-разрядных двоичных чисел от 0 до 2n—1;
7. провести заполнение таблицы истинности по столбикам, выполняя логические операции в соответствии с установленной в п.4 последовательностью.
Наборы входных переменных, во избежание ошибок, рекомендуют перечислять следующим образом:
а) определить количество наборов входных переменных;
б) разделить колонку значений первой переменной пополам и заполнить верхнюю часть колонки 0, а нижнюю — 1;
в) разделить колонку значений второй переменной на четыре части и заполнить каждую четверть чередующимися группами 0 или 1, начиная с группы 0;
г) продолжать деление колонок значений последующих переменных на 8, 16 и т.д. частей и заполнение их группами 0 или 1 до тех пор, пока группы 0 и 1 не будут состоять из одного символа.
Пример. Для формулы A&(B Ú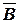 
& 
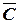) построить таблицу истинности алгебраически и с использованием электронных таблиц.
Количество логических переменных 3, следовательно, количество строк в таблице истинности должно быть 23 = 8.
Количество логических операций в формуле 5, следовательно, количество столбцов в таблице истинности должно быть 3 + 5 = 8.
| A | B | C |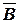
|
| &
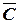
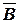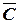
| B Ú ( & )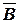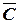
| A &(B Ú &  )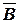
|
| 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 |
| 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 0 | 0 | 1 | 0 |
| 1 | 0 | 0 | 1 | 1 | 1 | 1 | 1 |
| 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | 0 | 0 | 0 | 1 | 1 |
Например, для формулы 
таблица истинности имеет вид:
| X | Y |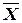 
| 
| 
| 
| 
|
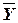
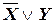
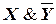
| 1 1 0 0 | 1 0 1 0 | 0 0 1 1 | 0 1 0 1 | 1 0 1 1 | 0 1 0 0 | 0 1 0 0 |
Легко видеть, что если формула содержит n элементарных высказываний, то она принимает 2n значений, состоящих из нулей и единиц, или, что то же, таблица содержит 2n строк.
6.4. Логические законы и правила преобразования логических выражений
Логические выражения называются равносильными, если их истинностные значения совпадают при любых значениях, входящих в них логических переменных.
Определение 6.1.
Две формулы алгебры логики А и В называются РАВНОСИЛЬНЫМИ, если они принимают одинаковые логические значения на любом наборе входящих в формулы элементарных высказываний. Равносильность формул будем обозначать знаком º, а запись А º В означает, что формулы А и В равносильны.
Формула А называется ТОЖДЕСТВЕННО ИСТИННОЙ (или ТАВТОЛОГИЕЙ), если она принимает значение 1 при всех значениях входящих в неё переменных.
Формула называется ТОЖДЕСТВЕННО ЛОЖНОЙ (или ПРОТИВОРЕЧИЕМ), если она принимает значение 0 при всех значениях входящих в неё переменных.
Между понятиями равносильности и эквивалентности существует следующая связь: если формулы А и В равносильны, то формула А«В – тавтология, и обратно, если формула А«В – тавтология, то формулы А и В равносильны.
В алгебре логики имеется ряд законов (основные равносильности), позволяющих производить равносильные преобразования логических выражений. Приведем соотношения, отражающие эти законы.
Закон двойного отрицания:
А =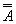 
.
Двойное отрицание исключает отрицание.
2. Переместительный (коммутативный) закон:
— для логического сложения:
А Ú B = B Ú A ;
— для логического умножения:
A & B = B & A ;
— для эквивалентности:
A ~ B = B ~ A ;
— для сложения по модулю два:
A Å B = B Å A .
Результат операции над высказываниями не зависит от того, в каком порядке берутся эти высказывания.
3. Сочетательный (ассоциативный) закон:
— для логического сложения:
( A Ú B ) Ú C = A Ú ( B Ú C );
— для логического умножения:
( A & B )& C = A &( B & C );
— для эквивалентности:
( A ~ B ) ~ С = A ~ ( B ~ С) ;
— для сложения по модулю два:
( A Å B ) Å С = A Å ( B Å С) .
При одинаковых знаках скобки можно ставить произвольно или вообще опускать.
4. Распределительный (дистрибутивный) закон:
— для логического сложения:
( A Ú B )& C = ( A & C ) Ú ( B & C );
— для логического умножения:
( A & B ) Ú C = ( A Ú C )&( B Ú C );
— для сложения по модулю два:
( A Å B )& C = ( A & C ) Å ( B & C ).
Определяет правило выноса общего высказывания за скобку.
5. Закон общей инверсии (законы де Моргана):
— для логического сложения:
;
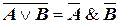— для логического умножения:
.
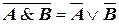6. Закон идемпотентности (от латинских слов idem — тот же самый и potens —сильный; дословно — равносильный):
— для логического сложения:
A Ú A = A ;
— для логического умножения:
A & A = A .
Закон означает отсутствие показателей степени.
7. Законы исключения констант:
— для логического сложения:
A Ú 1 = 1, A Ú 0 = A ;
— для логического умножения:
A &1 = A , A &0 = 0.
8. Закон противоречия:
A &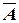 
= 0.
Невозможно, чтобы противоречащие высказывания были одновременно истинными.
9. Закон исключения третьего:
A Ú 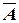= 1.
Из двух противоречащих высказываний об одном и том же предмете одно всегда истинно, а второе — ложно, третьего не дано.
10. Закон поглощения:
— для логического сложения:
A Ú ( A & B ) = A ;
— для логического умножения:
A &( A Ú B ) = A .
11. Закон исключения (склеивания):
— для логического сложения:
( A & B ) Ú ( 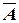& B ) = B ;
— для логического умножения:
( A Ú B )&( 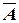Ú B ) = B .
12. Закон контрапозиции (правило перевертывания):
( A Þ B ) = ( B Þ A ).
Справедливость приведенных законов можно доказать табличным способом: выписать все наборы значений А и В, вычислить на них значения левой и правой частей доказываемого выражения и убедиться, что результирующие столбцы совпадут.
Докажем ( A Ú B )& C = ( A & C ) Ú ( B & C ), построив таблицы истинности левой и правой части формулы.
|
Дата: 2018-11-18, просмотров: 233.
