1. Логическая операция КОНЪЮНКЦИЯ (лат. conjunctio — связываю):
· в естественном языке соответствует союзу и;
· обозначения: &, Ç;
· в языках программирования обозначение: and;
· иное название: логическое умножение.
Конъюнкция — это логическая операция, ставящая в соответствие каждым двум простым высказываниям составное высказывание, являющееся истинным тогда и только тогда, когда оба исходных высказывания истинны.
| А | B | А &В |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Например, для высказываний «6 делится на 2», «6 делится на 3» их конъюнкцией будет высказывание «6 делится на 2 и 6 делится на 3», которое, очевидно, истинно.
Из определения операции конъюнкции видно, что союз «и» в алгебре логики употребляется в том же смысле, что и в повседневной речи. Но в обычной речи не принято соединять союзом «и» два высказывания, далекие друг от друга по содержанию, а в алгебре логики рассматривается конъюнкция двух любых высказываний. (Например: «В огороде бузина и в Киеве дядька»).
2. Логическая операция ДИЗЪЮНКЦИЯ (лат. disjunctio — различаю):
· в естественном языке соответствует союзу или;
· обозначение: Ú , È ;
· в языках программирования обозначение: or;
· иное название: логическое сложение.
Дизъюнкция — это логическая операция, которая каждым двум простым высказываниям ставит в соответствие составное высказывание, являющееся ложным тогда и только тогда, когда оба исходных высказывания ложны и истинным, когда хотя бы одно из двух образующих его высказываний истинно.
| А | В | А Ú В |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Например, высказывание «В треугольнике DFE угол D или угол E острый истинно, так как обязательно истинно одно из высказываний: «В треугольнике DFE угол D острый», «В треугольнике DFE угол E острый». В повседневной речи союз «или» употребляется в различном смысле: исключающем и не исключающем. В алгебре логики союз «или» всегда употребляется в не исключающем смысле.
3. Логическая операция ИМПЛИКАЦИЯ (лат. implicatio — тесно связываю):
· в естественном языке соответствует обороту «Если ..., то ...»;
· обозначение: Þ , ® ;
· иное название: логическое следование.
Импликация — это логическая операция, ставящая в соответствие каждым двум простым высказываниям составное высказывание, являющееся ложным тогда и только тогда, когда условие (первое высказывание) истинно, а следствие (второе высказывание) ложно.
| A | В | А Þ В |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Например, высказывание “если число 12 делится на 6, то оно делится на 3”, очевидно, истинно, так как здесь истинна посылка “ Число 12 делится на 6” и истинно заключение “Число 12 делится на 3”.
Употребление слов “если…, то…” в алгебре логики отличается от употребления их в обыденной речи, где мы, как правило, считаем, что, если высказывание х ложно, то высказывание “Если х, то y” вообще не имеет смысла. Кроме того, строя предложение вида “ если х, то y” в обыденной речи, мы всегда подразумеваем, что предложение y вытекает из предложения х. Употребление слов “если…, то…” в математической логике не требует этого, поскольку в ней смысл содержания высказываний не рассматривается.
Импликация играет важную роль в математических доказательствах, так как многие теоремы формулируются в условной форме “Если х, то y”. Если при этом известно, что х истинно, и доказана истинность импликации 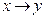 , то мы вправе сделать вывод об истинности заключения y.
, то мы вправе сделать вывод об истинности заключения y.
4. Логическая операция ЭКВИВАЛЕНТНОСТЬ (эквиваленция) (лат. аequivalens — равноценное):
· в естественном языке соответствует оборотам речи тогда и только тогда и в том и только в том случае;
· обозначение: Û , «, ~ ;
· иное название: равнозначность.
Эквивалентность – это логическая операция, ставящая в соответствие каждым двум простым высказываниям составное высказывание, являющееся истинным тогда и только тогда, когда оба исходных высказывания одновременно истинны или одновременно ложны.
| А | В | А ~ В |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Например, эквиваленция “Треугольник SPQ с вершиной S и основанием PQ равнобедренный тогда и только тогда, когда 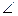 P =
P = 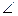 Q” является истинной, так как высказывания “Треугольник SPQ с вершиной S и основанием PQ равнобедренный” и “В треугольнике SPQ с вершиной S и основанием PQ”
Q” является истинной, так как высказывания “Треугольник SPQ с вершиной S и основанием PQ равнобедренный” и “В треугольнике SPQ с вершиной S и основанием PQ” 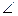 P =
P = 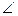 Q” либо одновременно истинны, либо одновременно ложны.
Q” либо одновременно истинны, либо одновременно ложны.
Эквивалентность играет большую роль в математических доказательствах. Известно, что значительное число теорем формулируется в форме необходимых и достаточных условий, т.е. в форме эквивалентности. В этом случае, зная об истинности или ложности одного их двух членов эквивалентности и доказав истинность самой эквивалентности, мы делаем заключение об истинности или ложности второго члена эквивалентности.
5. Логическая операция СЛОЖЕНИЕ ПО МОДУЛЮ ДВА:
· обозначение: Å , + ;
· вычисление значений: значения простых высказываний складываются арифметически, результат делиться на 2 нацело, в качестве значения операции берется остаток от деления.
Сложение по модулю два — это логическая операция, ставящая в соответствие каждым двум простым высказываниям составное высказывание, являющееся истинным тогда и только тогда, когда одно из двух образующих его высказываний истинно, а другое – ложно, и ложным, когда оба высказывания либо истины, либо ложны.
| A | В | А Å В |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
6. Логическая операция ОТРИЦАНИЕ.
Отрицанием высказывания Х называется новое высказывание, которое является истинным, если высказывание Х ложно, и ложным, если высказывание х истинно.
Отрицание высказывания Х обозначается 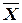 и читается «не Х» или «неверно, что Х». Логические значения высказывания
и читается «не Х» или «неверно, что Х». Логические значения высказывания 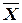 можно описать с помощью таблицы:
можно описать с помощью таблицы:
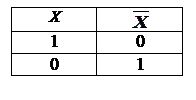
Пусть Х высказывание. Так как 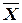 также является высказыванием, то можно образовать отрицание высказывания
также является высказыванием, то можно образовать отрицание высказывания 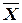 , то есть высказывание
, то есть высказывание 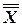 , которое называется ДВОЙНЫМ ОТРИЦАНИЕМ высказывания Х. Ясно, что логические значения высказываний
, которое называется ДВОЙНЫМ ОТРИЦАНИЕМ высказывания Х. Ясно, что логические значения высказываний 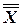 и Х совпадают.
и Х совпадают.
Например, для высказывания «Река Волхов вытекает из озера Ильмень» отрицанием будет высказывание «Неверно, что река Волхов вытекает из озера Ильмень» или «Река Волхов не вытекает из озера Ильмень», а двойным отрицанием будет высказывание «Неверно, что река Волхов не вытекает из озера Ильмень».
7. Логическая операция Стрелка Пирса « ¯ » — отрицание конъюнкции.
| A | В | А ¯ В |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
8. Логическая операция Штрих Шеффера «/» — отрицание дизъюнкции.
| A | В | А / В |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
Логические операции имеют следующий приоритет: действия в скобках, отрицание, &, Ú , Þ , Û , Å, ¯, /.
Пример. Определите истинность простых высказываний:
А = {Принтер – устройство вывода информации},
В = {Процессор – устройство хранения информации},
С = {Монитор – устройство вывода информации},
D = {Клавиатура – устройство обработки информации}.
Определите истинность составного высказывания: ( 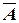 &
& 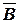 ) & (C Ú D ).
) & (C Ú D ).
На основании знания устройства компьютера устанавливаем истинность простых высказываний: А = 1, В = 0, С = 1, D = 0.
Определим сначала истинность составного высказывания, используя таблицы истинности логических операций:
( 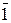 &
& 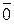 ) & (1 Ú 0) = (0&1) & (1 Ú 0) = (0 & 1) & (1 Ú 0) = 0 & 1 = 0.
) & (1 Ú 0) = (0&1) & (1 Ú 0) = (0 & 1) & (1 Ú 0) = 0 & 1 = 0.
Дата: 2018-11-18, просмотров: 366.