Алгебра высказываний
Алгебра в широком смысле этого слова наука об общих операциях, аналогичных сложению и умножению, которые могут выполняться не только над числами, но и над другими математическими объектами.
Примеры алгебр: алгебра натуральных чисел, алгебра рациональных чисел, алгебра многочленов, алгебра векторов, алгебра матриц, алгебра множеств и т.д. Объектами алгебры логики или булевой алгебры являются высказывания.
Высказывание — это любое предложение какого-либо языка (утверждение), содержание которого можно определить как истинное или ложное.
В естественном языке высказывания выражаются повествовательными предложениями. Восклицательные и вопросительные предложения высказываниями не являются.
Высказывания могут выражаться с помощью математических, физических, химических и прочих знаков. Из двух числовых выражений можно составить высказывания, соединив их знаками равенства или неравенства.
Приведем примеры высказываний:
1) Новгород стоит на Волхове.
2) Париж – столица Англии.
3) Карась не рыба.
4) Число 6 делится на 2 и на 3.
5) Если юноша окончил среднюю школу, то он получает аттестат зрелости.
Высказывания 1), 4), 5) истинны, а 2) и 3) – ложны.
Очевидно, предложение «Да здравствуют наши спортсмены!» не является высказыванием.
Высказывание, представляющее собой одно утверждение, принято называть простым или элементарным. Примерами элементарных высказываний могут служить высказывания 1) и 2).
Высказывания, которые получаются из элементарных с помощью грамматических связок «не», «и», «или», «если …, то …», «тогда и только тогда», принято называть сложными или составными. Так, высказывание 3) получается из простого высказывания «Карась – рыба» с помощью отрицания «не», высказывание 4) образовано из элементарных высказываний «Число 6 делится на 2», «Число 6 делится на 3», соединенных союзом «и». Высказывание 5) получается из простых высказываний «Юноша окончил среднюю школу», «Юноша получает аттестат зрелости» с помощью грамматической связки «если …, то …». Аналогично сложные высказывания могут быть получены из простых высказываний с помощью грамматических связок «или», «тогда и только тогда».
В алгебре логики все высказывания рассматриваются только с точки зрения их логического значения, а от их житейского содержания отвлекаются. Считается, что каждое высказывание либо истинно, либо ложно и ни одно высказывание не может быть одновременно истинным и ложным.
Простые высказывания в алгебре логики обозначаются заглавными латинскими буквами:
А = {Аристотель — основоположник логики}
В = {На яблонях растут бананы}.
Обоснование истинности или ложности простых высказываний решается вне алгебры логики. Например, истинность или ложность высказывания: "Сумма углов треугольника равна 180 градусов" устанавливается геометрией, причем — в геометрии Евклида это высказывание является истинным, а в геометрии Лобачевского — ложным.
Истинному высказыванию ставится в соответствие 1, ложному — 0. Таким образом, А = 1, В = 0.
Алгебра логики отвлекается от смысловой содержательности высказываний. Ее интересует только один факт — истинно или ложно данное высказывание, что дает возможность определять истинность или ложность составных высказываний алгебраическими методами.
Определение 6.1.
Две формулы алгебры логики А и В называются РАВНОСИЛЬНЫМИ, если они принимают одинаковые логические значения на любом наборе входящих в формулы элементарных высказываний. Равносильность формул будем обозначать знаком º, а запись А º В означает, что формулы А и В равносильны.
Формула А называется ТОЖДЕСТВЕННО ИСТИННОЙ (или ТАВТОЛОГИЕЙ), если она принимает значение 1 при всех значениях входящих в неё переменных.
Формула называется ТОЖДЕСТВЕННО ЛОЖНОЙ (или ПРОТИВОРЕЧИЕМ), если она принимает значение 0 при всех значениях входящих в неё переменных.
Между понятиями равносильности и эквивалентности существует следующая связь: если формулы А и В равносильны, то формула А«В – тавтология, и обратно, если формула А«В – тавтология, то формулы А и В равносильны.
В алгебре логики имеется ряд законов (основные равносильности), позволяющих производить равносильные преобразования логических выражений. Приведем соотношения, отражающие эти законы.
Закон двойного отрицания:
А =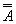 
.
Двойное отрицание исключает отрицание.
2. Переместительный (коммутативный) закон:
— для логического сложения:
А Ú B = B Ú A ;
— для логического умножения:
A & B = B & A ;
— для эквивалентности:
A ~ B = B ~ A ;
— для сложения по модулю два:
A Å B = B Å A .
Результат операции над высказываниями не зависит от того, в каком порядке берутся эти высказывания.
3. Сочетательный (ассоциативный) закон:
— для логического сложения:
( A Ú B ) Ú C = A Ú ( B Ú C );
— для логического умножения:
( A & B )& C = A &( B & C );
— для эквивалентности:
( A ~ B ) ~ С = A ~ ( B ~ С) ;
— для сложения по модулю два:
( A Å B ) Å С = A Å ( B Å С) .
При одинаковых знаках скобки можно ставить произвольно или вообще опускать.
4. Распределительный (дистрибутивный) закон:
— для логического сложения:
( A Ú B )& C = ( A & C ) Ú ( B & C );
— для логического умножения:
( A & B ) Ú C = ( A Ú C )&( B Ú C );
— для сложения по модулю два:
( A Å B )& C = ( A & C ) Å ( B & C ).
Определяет правило выноса общего высказывания за скобку.
5. Закон общей инверсии (законы де Моргана):
— для логического сложения:
;
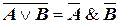— для логического умножения:
.
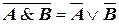6. Закон идемпотентности (от латинских слов idem — тот же самый и potens —сильный; дословно — равносильный):
— для логического сложения:
A Ú A = A ;
— для логического умножения:
A & A = A .
Закон означает отсутствие показателей степени.
7. Законы исключения констант:
— для логического сложения:
A Ú 1 = 1, A Ú 0 = A ;
— для логического умножения:
A &1 = A , A &0 = 0.
8. Закон противоречия:
A &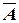 
= 0.
Невозможно, чтобы противоречащие высказывания были одновременно истинными.
9. Закон исключения третьего:
A Ú 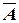= 1.
Из двух противоречащих высказываний об одном и том же предмете одно всегда истинно, а второе — ложно, третьего не дано.
10. Закон поглощения:
— для логического сложения:
A Ú ( A & B ) = A ;
— для логического умножения:
A &( A Ú B ) = A .
11. Закон исключения (склеивания):
— для логического сложения:
( A & B ) Ú ( 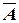& B ) = B ;
— для логического умножения:
( A Ú B )&( 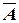Ú B ) = B .
12. Закон контрапозиции (правило перевертывания):
( A Þ B ) = ( B Þ A ).
Справедливость приведенных законов можно доказать табличным способом: выписать все наборы значений А и В, вычислить на них значения левой и правой частей доказываемого выражения и убедиться, что результирующие столбцы совпадут.
Докажем ( A Ú B )& C = ( A & C ) Ú ( B & C ), построив таблицы истинности левой и правой части формулы.
|
Определение 6.4
Функцией алгебры логики n переменных (или функций Буля) называется функция n переменных, где каждая переменная принимает два значения: 0 и 1, и при этом функция может принимать только одно из двух значений: 0 или 1.
Будем обозначать булевы функции большими латинскими буквами.
Ясно, что тождественно истинные и тождественно ложные формулы алгебры логики представляют собой постоянные функции, а две равносильные функции выражают одну и ту же функцию.
Выясним, каково число функций n переменных. Очевидно, каждую функцию алгебры логики (как и формулу алгебры логики) можно задать с помощью таблицы истинности, которая будет содержать 2n строк. Следовательно, каждая функция n переменных принимает 2n значений, состоящих из нулей и единиц. Таким образом, функция n переменных полностью определяется набором значений из нулей и единиц длины 2n. Общее же число наборов, состоящих из нулей и единиц, длины 2n равно 22n. Значит, число различных функций алгебры логики n переменных равно 22n.
В частности, различных функций одной переменной четыре, а различных функций двух переменных шестнадцать.
Булевы функции, зависящие от одной переменной, называются одноместными.
| ||||||||
Отрицание
| х | F( х ) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 0 | 0 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1 | 1 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Решение логических задач
Логические задачи Для решения многих логических задач необходимо: 1) выделить элементарные (простые) высказывания и обозначить их буквами; 2) записать условие задачи на языке алгебры логики, соединив простые высказывания в сложные с помощью логических операций; 3) составить единое логическое выражение для всех требований задачи; 4) используя законы алгебры логики попытаться упростить полученное выражение и вычислить все его значения либо построить таблицу истинности для рассматриваемого выражения; 5) выбрать решение — набор значений простых высказываний, при котором логическое выражение является истинным; 6) проверить, удовлетворяет ли полученное решение условию задачи. Еще один способ решения логических задач заключается в том, чтобы по условию задачи составить таблицу истинности. Анализ полученной таблицы истинности зачастую позволяет получить требуемый результат. Примеры задач 1. Задача. Компьютер вышел из строя (нет изображения на экране монитора), однако неизвестно какое устройство не работает (монитор, видеокарта или оперативная память). Можно предположить следующее: 1) Если монитор исправен или видеокарта неисправна, то оперативная память неисправна; 2) Если монитор исправен, то оперативная память исправна. Исправен ли монитор?
Решение
1. Рассмотрим простые высказывания: А = {Монитор неисправен}, В = { Видеокарта неисправна}, С = { Оперативная память неисправна}. 2. Запишем на языке алгебры логики наши предположения: ( 3. Пусть F ( A , B , C ) = (( 4. Составим для данного высказывания таблицу истинности:
5. Решить данную задачу — значит указать, при каких значениях А полученное сложное высказывание истинно. Необходимо проанализировать все строки таблицы истинности, где F = 1. Анализ таблицы показывает, что сложное высказывание истинно во всех случаях, когда А — истинно, т. е. вероятнее всего неисправен именно монитор. 2. Задача: "Финансовый прогноз" Три подразделения — A, B, C — торговой фирмы стремились получить по итогам года максимальную прибыль. Экономисты высказали следующие предположения: 1. A получит максимальную прибыль только тогда, когда получат максимальную прибыль B и C. 2. Либо A и B, получат максимальную прибыль одновременно, либо одновременно не получат. 3. Для того чтобы С получило максимальную прибыль, необходимо, чтобы и В получило максимальную прибыль. По завершении года оказалось, что одно из трех предположений ложно. Какие из названных подразделений получили максимальную прибыль? Решение Рассмотрим простые высказывания: А = {А получит максимальную прибыль}; B = {В получит максимальную прибыль}; С = {С получит максимальную прибыль}; Запишем на языке алгебры логики прогнозы, высказанные экономистами: 1) F1 = A 2) F2 = A & C V A & C; 3) F3 = C Теперь составим таблицу истинности для F1, F2, F3.
Где 0 — "ложь" , 1 — "истина". Теперь вспомним, что ложным оказался один из прогнозов — F1, F2, F3. Эта ситуация соответствует четвертой строке таблицы. Ответ: B и С получат максимальную прибыль.
3. Задача. По обвинению в ограблении перед судом предстали Иванов, Петров, Сидоров. Следствие установлено следующее: 1. Если Иванов не виновен или Петров виновен, то Сидоров виновен. 2. Если Иванов не виновен, то Сидоров не виновен. Виновен ли Иванов? Решение Рассмотрим простые высказывания: A = {Иванов виновен} B = {Петров виновен} C = {Сидоров виновен}. Запишем на языке алгебры логики факты, установленные следствием:
Пусть
Решить задачу – это значит указать, при каких значениях А это сложное высказывание истинно, и если хотя бы в одном случае (при разных B и C) F = 1 A = 0 (Иванов не виновен), то у следствия недостаточно фактов для того, чтобы обвинять Иванова в преступлении. Таблица истинности
Из таблицы истинности видно, что сложное высказывание истинно только когда A — истинно, т.е. Иванов виновен в ограблении.
4. Задача “КОМИССАР МЕГРЭ” Мегрэ, вернувшись домой, позвонил на набережную Орфевр. — Говорит Мегрэ. Есть новости? — Да, шеф. Поступили сообщения от инспекторов. Торранс установил, что если Франсуа был пьян, то либо Этьен убийца, либо Франсуа лжет. Жуссье считает, что или Этьен убийца, или Франсуа не был пьян, и убийство произошло после полуночи. Инспектор Люка просил передать вам, что если убийство произошло после полуночи, то либо Этьен убийца, либо Франсуа лжет. Затем звонила… — Все. Спасибо. Этого достаточно. — Комиссар положил трубку. Он знал, что трезвый Франсуа никогда не лжет. Теперь он знал все. Решение Рассмотрим следующие простые высказывания: А = {Франсуа был пьян}, В = {Этьен убийца}, С = {Франсуа лжет}, D = {убийство произошло после полуночи}. Перепишем на языке алгебры логики условие задачи. Инспектора комиссара Мегрэ установили, что А Þ (В Ú С) = 1, В Ú (А & D) = 1, D Þ (В Ú С) = 1. Сам Мегрэ знает, что А & С = 1. Истинной будет и конъюнкция четырех высказываний: (A Þ (B Ú C) & (B Ú (A & D)) & (D Þ (B Ú C)) & ( A & C). Ответ: Франсуа был пьян, Этьен убийца, Франсуа лжет, убийство произошло после полуночи. 5. Задача. Виктор, Роман, Леонид и Сергей заняли на математической олимпиаде четыре первых места. Когда их спросили о распределении мест, они дали три таких ответа: 1. Сергей — первый, Роман — второй; 2. Сергей — второй, Виктор — третий; 3. Леонид — второй, Виктор — четвертый. Известно, что в каждом ответе только одно утверждение истинно. Как распределились места? Решение Рассмотрим простые высказывания: С1 = (Сергей занял первое место), Р2 = (Роман занял второе место), С2 = (Сергей занял второе место), В3 = (Виктор занял третье), Л2 = (Леонид занял второе место), В4 = (Виктор занял четвертое место). На языке алгебры логики ответы ребят можно записать следующим образом: С1 Ú Р2 = 1, С2 Ú В3 = 1, Л2 Ú В4 = 1. Конъюнкция истинных высказываний истинна. Следовательно, имеет место равенство: (С1 Ú Р2) & (С2 Ú В3) & (Л2 Ú В4 ) = 1. Раскроем скобки: С1&С2&Л2 Ú C2&Р2&Л2 Ú С1&В3&Л2 Ú Р2&В3&Л2 Ú С1&С2&В4 Ú 0 0 1 0 0 Ú С2&Р2&В4 Ú С1&В3&В4 Ú Р2&В3&В4 0 0 0 Нули в равенстве означают, что получились несовместимые условия, исходя из того, что участник математической олимпиаде не может одновременно занимать несколько мест и каждое место распределяется одному участнику. Единственное выражение, значение которого может быть истинным это С1&В3&Л2 = 1.
Другими словами, места на олимпиаде распределились так: Сергей — 1-е место, Леонид — 2-е место, Виктор — 3-е место, Роман — 4-е место.
6. Задача. Алеша, Боря и Гриша нашли в земле старинный сосуд. Рассматривая удивительную находку, каждый высказал по два предложения: Алеша: “Это сосуд греческий и изготовлен в V веке”. Боря: “Это сосуд финикийский и изготовлен в III веке”. Гриша: “Это сосуд не греческий и изготовлен в IV веке”. Учитель истории сказал ребятам, что каждый из них прав только в одном из двух предположений. Где и в каком веке изготовлен сосуд? Решение Рассмотрим простые высказывания: А = (сосуд греческий), В = (сосуд финикийский), С = (сосуд изготовлен в III веке), D = (сосуд изготовлен в IV веке), Е = (сосуд изготовлен в V веке ). Запишем предположения школьников на языке алгебры логики. А Ú Е = 1 (слова Алеша), В Ú С = 1 (слова Бори),
Если все эти высказывания логически перемножить, то получится истинное сложное высказывание: ( A Ú E ) & (B Ú C) & ( Раскроем скобки: A&B & 0 1 0 0 0 0 Ú D&A&C Ú D&E&C. 0 0 Исходя из того, что сосуд мог быть изготовлен только в одной стране и в одном веке, нули в равенстве означают, что получились несовместимые условия. Единственное выражение, значение которого может быть истинным это E&B& Мы установили, что сосуд финикийский и изготовлен в V веке, что удовлетворяет условию задачи.
Глава VI. Элементы математической логики С момента зарождения теоретической науки в 6-5 вв. до н.э. (особенно в Древней Греции) были подвергнуты исследованию методы рассуждений, применяемые для убедительного обоснования утверждений. Так начала складываться наука логика. Установившиеся в Греции демократические формы жизни потребовали развития искусства убеждения — ораторского искусства, риторики. Появились учителя риторики — софисты, учившие не только доказывать истинные утверждения, но и искусно их опровергать. Понятия истины, лжи и противоречия, а также причины истинности или ложности заключений, полученных из истинных посылок, надолго стали предметом изучения в логике.
Стройную научную систему логики впервые разработал великий греческий учёный Аристотель (ученик Платона, воспитатель Александра Македонского). В своём логическом своде «Органон» («Категории», «Об истолковании», «Аналитики» 1-я и 2-я, «Топика») он создал раздел формальной логики силлогистику. Его труды оказали влияние на развитие логической науки во всём мире. В Европе до 17 века вся логика развивалась на основе аристотелевского учения.
Первые значительные попытки превращения логики в математическую науку сделал великий немецкий учёный и политический деятель Готфрид Вильгельм Лейбниц (1646-1716). Однако решающего успеха в этом направлении добился в 1847 году английский математик Джордж Буль (1815-1864), построив алгебру логики, названную в его честь булевой. Основными разделами современной математической логики (её классического варианта) являются логика высказываний, идущая от Дж. Буля и не охватывающая силлогистику Аристотеля, и значительно более широкая логика предикатов, содержащая силлогистику как часть. Современный вид математическая логика приобрела в 1880-е годы в трудах немецкого логика, математика и философа Готлоба Фреге (1848-1925). Он дал первую аксиоматику логики высказываний и предикатов и сделал попытку свести математику к логике. Логика — наука, изучающая законы и формы мышления; учение о способах рассуждений и доказательств. Законы мира, сущность предметов, общее в них мы познаем посредством абстрактного мышления. Основными формами абстрактного мышления являются понятия, суждения и умозаключения. Понятие — форма мышления, в которой отражаются существенные признаки отдельного предмета или класса однородных предметов. Понятия в языке выражаются словами. Содержание понятия — совокупность существенных признаков, отраженных в этом понятии. Объем понятия — множество предметов, каждому из которых принадлежат признаки, составляющие содержание понятия. Выделяют понятия общие и единичные. Суждение — это форма мышления, в которой что-либо утверждается или отрицается о предметах, признаках или их отношениях. Умозаключение — форма мышления, посредством которой из одного или нескольких суждений, называемых посылками, мы по определенным правилам вывода получаем суждение-заключение.
Алгебра высказываний Алгебра в широком смысле этого слова наука об общих операциях, аналогичных сложению и умножению, которые могут выполняться не только над числами, но и над другими математическими объектами. Примеры алгебр: алгебра натуральных чисел, алгебра рациональных чисел, алгебра многочленов, алгебра векторов, алгебра матриц, алгебра множеств и т.д. Объектами алгебры логики или булевой алгебры являются высказывания. Высказывание — это любое предложение какого-либо языка (утверждение), содержание которого можно определить как истинное или ложное. В естественном языке высказывания выражаются повествовательными предложениями. Восклицательные и вопросительные предложения высказываниями не являются. Высказывания могут выражаться с помощью математических, физических, химических и прочих знаков. Из двух числовых выражений можно составить высказывания, соединив их знаками равенства или неравенства. Приведем примеры высказываний: 1) Новгород стоит на Волхове. 2) Париж – столица Англии. 3) Карась не рыба. 4) Число 6 делится на 2 и на 3. 5) Если юноша окончил среднюю школу, то он получает аттестат зрелости.
Высказывания 1), 4), 5) истинны, а 2) и 3) – ложны. Очевидно, предложение «Да здравствуют наши спортсмены!» не является высказыванием. Высказывание, представляющее собой одно утверждение, принято называть простым или элементарным. Примерами элементарных высказываний могут служить высказывания 1) и 2). Высказывания, которые получаются из элементарных с помощью грамматических связок «не», «и», «или», «если …, то …», «тогда и только тогда», принято называть сложными или составными. Так, высказывание 3) получается из простого высказывания «Карась – рыба» с помощью отрицания «не», высказывание 4) образовано из элементарных высказываний «Число 6 делится на 2», «Число 6 делится на 3», соединенных союзом «и». Высказывание 5) получается из простых высказываний «Юноша окончил среднюю школу», «Юноша получает аттестат зрелости» с помощью грамматической связки «если …, то …». Аналогично сложные высказывания могут быть получены из простых высказываний с помощью грамматических связок «или», «тогда и только тогда». В алгебре логики все высказывания рассматриваются только с точки зрения их логического значения, а от их житейского содержания отвлекаются. Считается, что каждое высказывание либо истинно, либо ложно и ни одно высказывание не может быть одновременно истинным и ложным. Простые высказывания в алгебре логики обозначаются заглавными латинскими буквами: А = {Аристотель — основоположник логики} В = {На яблонях растут бананы}. Обоснование истинности или ложности простых высказываний решается вне алгебры логики. Например, истинность или ложность высказывания: "Сумма углов треугольника равна 180 градусов" устанавливается геометрией, причем — в геометрии Евклида это высказывание является истинным, а в геометрии Лобачевского — ложным. Истинному высказыванию ставится в соответствие 1, ложному — 0. Таким образом, А = 1, В = 0. Алгебра логики отвлекается от смысловой содержательности высказываний. Ее интересует только один факт — истинно или ложно данное высказывание, что дает возможность определять истинность или ложность составных высказываний алгебраическими методами. Дата: 2018-11-18, просмотров: 251. 
Материалы представленные на сайте исключительно с целью ознакомления пользователям Интернета и не преследуют коммерческих целей или нарушение авторских прав.
© 2018 - 2024
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
.
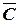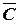
B & C;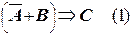
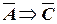
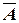
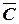
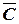
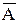Ú D = 1 (слова Гриши).
