Сегодня сложно представить себе ряд наук без применения комплексных чисел. Теория электротехники, электромеханики, радиотехники, самолетостроения и других наук невозможна без применения моделей в виде комплексных чисел. Экономика, более сложная наука, до сих пор не знала применения комплексных чисел.
Товар является носителем двух составляющих: потребительских свойств, объективно присущих товару, и цены - денежной оценки потребительских свойств товара конкретным потребителем. С учетом того, что и потребительские свойства товара и его цена являются необходимыми показателями свойств товара, возникает потребность разработки и использования комплексного показателя, характеризующего эти две стороны одного объекта. Именно таким показателем может стать комплексное число, состоящее из действительной и мнимой частей.
Представив какую-либо оценку потребительских свойств товара П как действительную часть комплексного числа, а его цену Ц - как мнимую часть, получим:
Т = П + iЦ, (1)
где i - мнимая единица, которая определяется условием i? (0, 1) и удовлетворяет соотношению:
i2 = -1. (2)
Легко убедиться в том, что запись (1) позволяет полностью описать свойства конкретного товара и математически корректно работать как с каждой из двух его составляющих, так и с их совокупностью в целом.
Раздел 5. Элементы теории вероятностей и математической статистики
Случайные события и их вероятности.
Применение комбинаторики к подсчету вероятности.
Пример 1:
В партии из N деталей имеется n бракованных. Какова вероятность того, что среди наудачу отобранных k деталей окажется s бракованных?
Решение.
Количество всех элементарных исходов равно 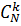 . Для подсчета числа благоприятных случаев рассуждаем так: из n бракованных можно выбрать s деталей
. Для подсчета числа благоприятных случаев рассуждаем так: из n бракованных можно выбрать s деталей 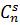 способами, а из N – n небракованных можно выбрать k – s небракованных деталей
способами, а из N – n небракованных можно выбрать k – s небракованных деталей 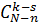 способами; по правилу произведения число благоприятных случаев равно
способами; по правилу произведения число благоприятных случаев равно 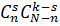 . Искомая вероятность равна:
. Искомая вероятность равна:
p = 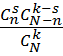 (1)
(1)
Замечание:
Всякое k-членное подмножество n-членного множества называется сочетанием из n элементов по k.
Число различных сочетаний из n элементов по k обозначается 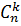 .
.
Справедлива формула
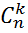 =
= 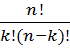 , (2)
, (2)
n! =1 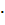 2
2 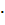 3
3 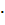 4
4 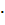 …
…  n
n
Пример 2:
В партии из 12 деталей имеется 7 стандартных. Найти вероятность того, что среди шести взятых наугад деталей 4 стандартных.
Решение.
Искомую вероятность найдем по формуле (1) для случая
N =12, n =7, k = 6, s = 4.
p = 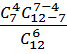 =
= 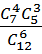 =
= 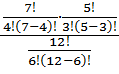 =
= 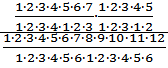
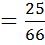 .
.
ЗАДАНИЯ КОНТРОЛЬНОЙ РАБОТЫ
Задание №1.
| Номер варианта | Задание: Найти произведение матриц АВ = С, если А, В даны: |
| 1 | А = 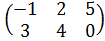 , В = , В = 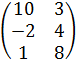
|
| 2 | А = 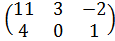 , В = , В = 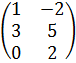
|
| 3 | А = 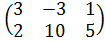 , В = , В = 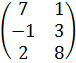
|
| 4 | А = 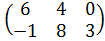 , В = , В = 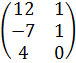
|
| 5 | А = 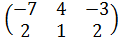 , В = , В = 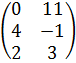
|
| 6 | А = 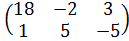 , В = , В = 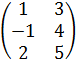
|
| 7 | А = 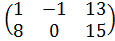 , В = , В = 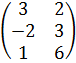
|
| 8 | А = 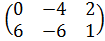 , В = , В = 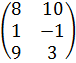
|
| 9 | А = 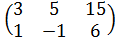 , В = , В = 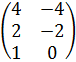
|
| 10 | А = 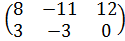 , В = , В = 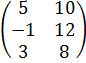
|
Задание №2.
| Номер варианта | Задание: Для множеств А и В найти: АUВ; А∩В; АΔВ; А\В; А×В; А×А; В2 . |
| 1 | А = 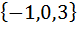 , В = , В = 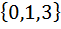
|
| 2 | А = 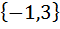 , В = , В = 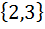
|
| 3 | А = 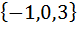 , В = , В = 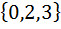
|
| 4 | А = 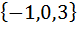 , В = , В = 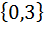
|
| 5 | А = 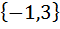 , В = , В = 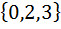
|
| 6 | А = 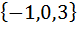 , В = , В = 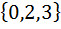
|
| 7 | А = 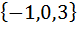 , В = , В = 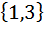
|
| 8 | А = 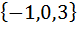 , В = , В = 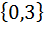
|
| 9 | А = 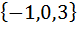 , В = , В = 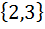
|
| 10 | А = 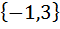 , В = , В = 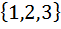
|
Задание №3.
| Номер варианта | Задание: Выполнить действия | |||
| 1 | (1+3i)+(-3+i) | (5-3i)×(2-5i) | (5+4i)-(-3+4i) | (2+3i)/(2-3i) |
| 2 | (-4+3i)+(4-3i) | (3+5i)×(2+3i) | (4+2i)-(-1+2i) | (5-4i)/(-3+2i) |
| 3 | (-2+5i)+(2-5i) | (3-4i)×( -7+3i) | (7-2i)-( -4+3i) | (-5+2i)/(6-7i) |
| 4 | (3-4i)+(-3+4i) | (6+7i)×(-5+2i) | (-9+4i)-( 3+5i) | (1+8i)/( -3+i) |
| 5 | (7-2i)+(-7+3i) | (1+8i)×(-9+4i) | (2+3i)-(-3+i) | (-8+i)/(7-2i) |
| 6 | (-5+2i)+(5-2i) | (3+4i)×( -8+i) | (-3+4i)-(6+7i) | (6-7i)/( -1+2i) |
| 7 | (-6+7i)+(6-7i) | (7-2i)×( -3+i) | (3+5i)-(-9+4i) | (3+4i)/( -5+2i) |
| 8 | (1+8i)+(-8+i) | (2+3i)×(6-7i) | (-5+2i)-(3+4i) | (-9+4i)/(5-7i) |
| 9 | (-9+4i)+(9-4i) | (-5+2i)×( 7-2i) | (-4+3i)-( 2+3i) | (6+7i)/( 1+8i) |
| 10 | (8-5i)+(-8+5i) | (-1+2i)×(6+7i) | (7-5i)-(-8+i) | (3+5i)/(-4+3i) |
З ада ние №4.
| № варианта | Задание: Исследовать свойства функции и построить её график |
| 1 | y = 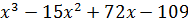
|
| 2 | y = 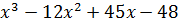
|
| 3 | y = 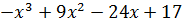
|
| 4 | y = 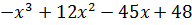
|
| 5 | y = 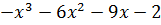
|
| 6 | y = 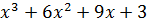
|
| 7 | y = 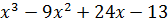
|
| 8 | y = 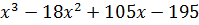
|
| 9 | y = 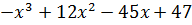
|
| 10 | y = 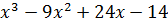
|
Задание №5.
| Номер варианта | Задание: Найти интегралы | ||
| 1 | 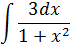
| 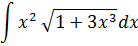
| 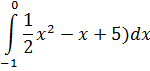
|
| 2 | 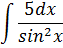
| 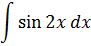
| 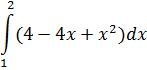
|
| 3 | 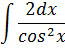
| 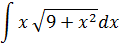
| 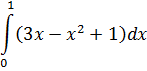
|
| 4 | 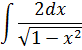
| 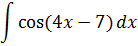
| 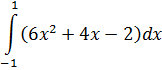
|
| 5 | 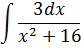
| 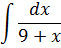
| 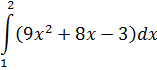
|
| 6 | 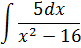
| 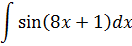
| 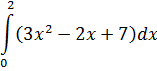
|
| 7 | 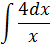
| 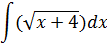
| 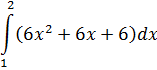
|
| 8 | 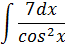
| 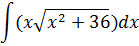
| 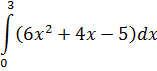
|
| 9 | 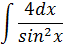
| 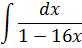
| 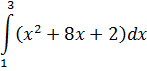
|
| 10 | 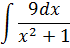
| 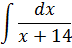
| 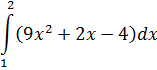
|
Задание №6.
| Номер варианта | Задание: Решить задачу |
| 1 | В партии из 8 деталей имеется 6 стандартных. Найти вероятность того, что среди пяти взятых наугад деталей ровно три стандартных. |
| 2 | В цехе работают 6 мужчин и 4 женщины. По табельным номерам наудачу отобраны 7 человек. Найти вероятность того, что среди отобранных лиц окажутся 3 женщины. |
| 3 | В группе 12 студентов, среди которых 8 отличников. По списку отобраны 9 студентов. Найти вероятность того, что среди отобранных студентов пять отличников. |
| 4 | В урне 5 белых и 4 черных шаров. Из урны наугад вынимают 3 шара. Найти вероятность того, что среди вынутых шаров будет 2 белых. |
| 5 | В партии из 10 деталей имеется 8 стандартных. Найти вероятность того, что среди 6 взятых наугад деталей ровно 4 стандартных. |
| 6 | В группе 16 студентов, среди которых 10 отличников. По списку отобраны 12 студентов. Найти вероятность того, что среди отобранных студентов 6 отличников |
| 7 | В цехе работают 7 мужчин и 5 женщин. По табельным номерам наудачу отобраны 8 человек. Найти вероятность того, что среди отобранных лиц окажутся 4 женщины. |
| 8 | В урне 7 белых и 5 черных шаров. Из урны наугад вынимают 6 шаров. Найти вероятность того, что среди вынутых шаров будет 4 белых. |
| 9 | В партии из 12 деталей имеется 8 стандартных. Найти вероятность того, что среди 7 взятых наугад деталей ровно 5 стандартных. |
| 10 | В группе 14 студентов, среди которых 9 отличников. По списку отобраны 11 студентов. Найти вероятность того, что среди отобранных студентов 5 отличников |
Дата: 2018-11-18, просмотров: 1091.