МЕТОДИЧЕСКИЕ УКАЗАНИЯ
ПО ВЫПОЛНЕНИЮ
ДОМАШНЕЙ КОНТРОЛЬНОЙ РАБОТЫ
по учебной дисциплине:
«Математика»
для студентов заочной формы обучения
Специальности 35.02.08 Электрификация и автоматизация сельского хозяйства
(на базе среднего общего образования)
Преподаватель: Лиховидова Елена Николаевна
Сергиев Посад
2017г
Данное методическое пособие содержит общие рекомендации по выполнению контрольной работы, краткие теоретические сведения, необходимые для выполнения контрольной работы, образцы решения задач, приведены примеры использования математических методов при решении задач, контрольные задания.
ПРИМЕРНЫЙ ТЕМАТИЧЕСКИЙ ПЛАН
Раздел 1. Элементы линейной алгебры
Тема 1.1 Матрицы и определители.
Тема 1.2. Системы линейных уравнений.
Раздел 2. Основы дискретной математики
Тема 2.1. Множества и отношения.
Тема 2.2. Основные понятия теории графов.
Раздел 3. Основы математического анализа
Тема 3.1. Теория пределов.
Тема 3.2. Дифференциальное исчисление.
Тема 3.3. Интегральное исчисление.
Раздел 4. Основы теории комплексных чисел
Тема 4.1. Основные понятия теории комплексных чисел.
Раздел 5. Элементы теории вероятностей и математической статистики
Тема 5.1. Случайные события и их вероятности.
Тема 5.2. Основы математической статистики.
ОБЩИЕ МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО
КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ И ОБРАЗЦЫ РЕШЕНИЯ ЗАДАЧ.
Раздел 1. Элементы линейной алгебры. Матрицы.
Матрица – это прямоугольная таблица каких-либо элементов. В качестве элементов мы будем рассматривать числа, то есть числовые матрицы. ЭЛЕМЕНТ – это термин. Термин желательно запомнить, он будет часто встречаться, не случайно я использовал для его выделения жирный шрифт.
Обозначение: матрицы обычно обозначают прописными латинскими буквами 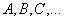
Пример: рассмотрим матрицу «два на три»:
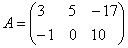
Данная матрица состоит из шести элементов:
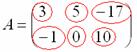
Все числа (элементы) внутри матрицы существуют сами по себе, то есть ни о каком вычитании речи не идет:
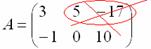
Это просто таблица (набор) чисел!
Рассматриваемая матрица имеет две строки:
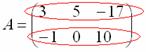
и три столбца:

СТАНДАРТ: когда говорят о размерах матрицы, то сначала указывают количество строк, а только потом – количество столбцов. Мы только что разобрали матрицу «два на три».
Если количество строк и столбцов матрицы совпадает, то матрицу называют квадратной, например: 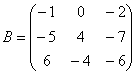 – матрица «три на три».
– матрица «три на три».
Если в матрице один столбец 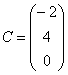 или одна строка
или одна строка 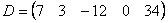 , то такие матрицы также называют векторами.
, то такие матрицы также называют векторами.
Действия с матрицами:
Умножение матрицы на число.
Пример:
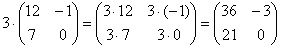
Для того чтобы умножить матрицу на число, нужно каждый элемент матрицы умножить на данное число. В данном случае – на тройку.
Сумма (разность) матриц.
Сумма матриц действие несложное.
НЕ ВСЕ МАТРИЦЫ МОЖНО СКЛАДЫВАТЬ. Для выполнения сложения (вычитания) матриц, необходимо, чтобы они были ОДИНАКОВЫМИ ПО РАЗМЕРУ.
Например, если дана матрица «два на два», то ее можно складывать только с матрицей «два на два» и никакой другой!
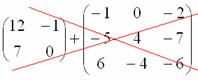
Пример:
Сложить матрицы 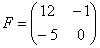 и
и 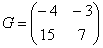
Для того чтобы сложить матрицы, необходимо сложить их соответствующие элементы:
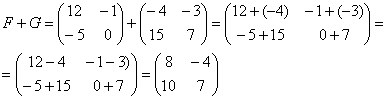
Для разности матриц правило аналогичное, необходимо найти разность соответствующих элементов.
Пример:
Найти разность матриц 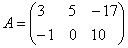 ,
, 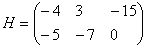
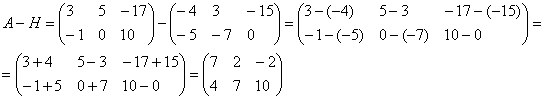
Умножение матриц.
Как умножить матрицы?
Начнем с самого простого:
Пример:
Умножить матрицу 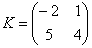 на матрицу
на матрицу 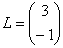
Сразу привожу формулу для каждого случая:
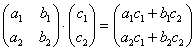 – попытайтесь сразу уловить закономерность.
– попытайтесь сразу уловить закономерность.
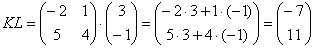
Пример сложнее:
Умножить матрицу 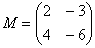 на матрицу
на матрицу 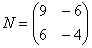
Формула: 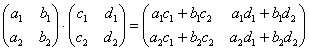
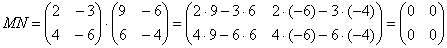
В результате получена так называемая нулевая матрица.
Попробуйте самостоятельно выполнить умножение 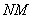 (правильный ответ
(правильный ответ 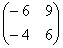 ).
).
Обратите внимание, что 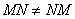 ! Таким образом, переставлять матрицы в произведении нельзя!
! Таким образом, переставлять матрицы в произведении нельзя!
Если в задании предложено умножить матрицу 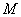 на матрицу
на матрицу 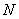 , то и умножать нужно именно в таком порядке. Ни в коем случае не наоборот.
, то и умножать нужно именно в таком порядке. Ни в коем случае не наоборот.
Переходим к матрицам третьего порядка:
Умножить матрицу 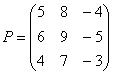 на матрицу
на матрицу 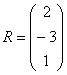
Формула очень похожа на предыдущие формулы:
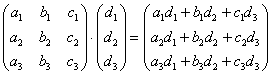
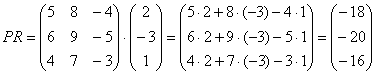
А теперь попробуйте самостоятельно разобраться в умножении следующих матриц:
Умножьте матрицу 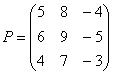 на матрицу
на матрицу 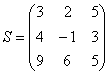
Вот готовое решение, но постарайтесь сначала в него не заглядывать!
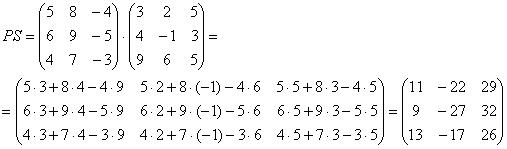
Пример 1
Пусть A = {1, 2, 3, 4, 5, 6, 7, 8, 9} и B = {1, 3, 5, 7, 9, 11, 13, 17, 19}. Найти AUB и A∩B
Решение
| AUB = {1, 2, 3, 4, 5, 6, 7, 8, 9, 11, 13, 17, 19}, A∩B = {1, 3, 5, 7, 9}.
Разностью множеств A и B называется множество A \ B, которое состоит из тех и только тех элементов, которые принадлежат множеству A, но не принадлежат множеству B.
Пример 2
Пусть A = {1, 2, 3, 4, 5, 6, 7, 8, 9} и B = {1, 3, 5, 7, 9, 11, 13, 17, 19}. Найти A \ B и B \ A.
Решение
А\В = {2,4,6,8}.
В\А = {11,13,17,19}.
|
Симметрической разностью множеств A и В называется множество
А Δ В, которое состоит из тех элементов, которые не являются общими для двух заданных множеств.
Пример 3.
Пусть А = {1,2,3,4,5}, В = {3,4,5,6,7}
Найти АΔВ.
Решение
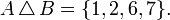
Декартовым произведением А×В множеств А,В называется множество всех упорядоченных пар (а,b) , где а 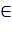 А , b
А , b 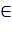 В. Кратко это записывают так А×В ={(а,b) , а
В. Кратко это записывают так А×В ={(а,b) , а 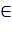 А , b
А , b 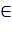 В}.
В}.
Декартовым квадратом множества А называют декартово произведение множества А на множество А (т.е. само на себя).
Если перемножаются одинаковые множества, используется обозначение степени:
An = A × A × A ×...× A
Пример 4.
Пусть А = {1,2}, В = {1,5,7}.
Найти А× В; А× А; В2.
Решение
А×В ={(1,1) , (1,5), (1,7), (2,1), (2,5), (2,7)}.
А× А = {(1,1), (1,2), (2,2), (2,1)}
В2 = {(1,1), (1,5), (1,7), (5,1), (5,5), (5,7), (7,1), (7, 5), (7,7)}.
Интегральное исчисление.
| 1.Основные правила интегрирования |
1. Если 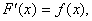 то то 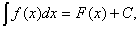 где где 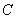 – произвольная постоянная.
2. – произвольная постоянная.
2. 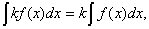 где где 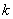 – постоянная.
3. – постоянная.
3. 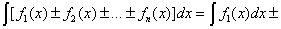
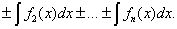
|
| 2.Таблица основных неопределенных интегралов |
1. 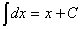 .
2. .
2. 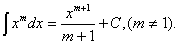 3.
3. 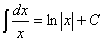 .
4. .
4. 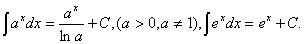 5.
5. 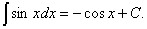 6.
6. 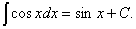 7.
7. 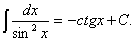 8.
8. 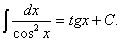 9.
9. 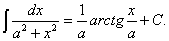 10.
10. 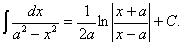 11.
11. 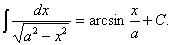 12.
12. 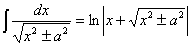 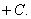
|
| 3.Непосредственное интегрирование |
Отыскание неопределенного интеграла с помощью таблицы, правил и тождественных преобразований называют непосредственным интегрированием.
Пример:
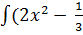 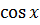 - - 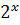 + + 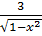 )dx = 2 )dx = 2 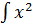 dx - dx -  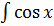 dx - dx - 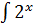 dx + 3 dx + 3 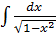 = 2 = 2 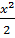 - -  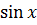 +3 arcsin x + C
При интегрировании использованы правила 2 и 3, а также табличные формулы 2,4,6,11. +3 arcsin x + C
При интегрировании использованы правила 2 и 3, а также табличные формулы 2,4,6,11.
|
| 4.Метод подстановки (замена переменной интегрирования) |
Замена переменной в неопределенном интеграле производится с помощью подстановок двух видов: а) 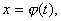 где где 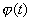 – монотонная, дифференцируемая функция; б) – монотонная, дифференцируемая функция; б) 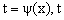 – новая переменная.
В первом случае формула замены переменной имеет вид: – новая переменная.
В первом случае формула замены переменной имеет вид:
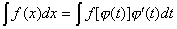 . (1)
Во втором случае: . (1)
Во втором случае:
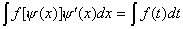 . (2)
В обоих случаях после интегрирования следует возвращаться к старой переменной обратной подстановкой.
Пример 1.
Вычислить интеграл: . (2)
В обоих случаях после интегрирования следует возвращаться к старой переменной обратной подстановкой.
Пример 1.
Вычислить интеграл:
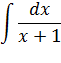 Решение.
Сделаем замену переменных t = x +1 и найдем дифференциал от обеих частей, тогда
dt = (x+1)'dx ⇒ dt= dx
Подставляя все в исходный интеграл, получим:
Решение.
Сделаем замену переменных t = x +1 и найдем дифференциал от обеих частей, тогда
dt = (x+1)'dx ⇒ dt= dx
Подставляя все в исходный интеграл, получим:
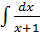 = = 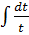 = = 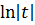 +C = +C = 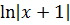 +C,
где C - const . Здесь заключительное действие - это обратная замена переменных.
В данном случае с помощью замены в интеграле удалось свести интеграл к табличному, затем была произведена обратная замена переменных и получен ответ. +C,
где C - const . Здесь заключительное действие - это обратная замена переменных.
В данном случае с помощью замены в интеграле удалось свести интеграл к табличному, затем была произведена обратная замена переменных и получен ответ.
|
Пример 2:
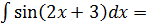 (положим t = 2x+3, тогда x=
(положим t = 2x+3, тогда x=  t-
t-  , dx =
, dx =  dt)
dt)
= 
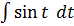 =-
=- 
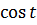 +C= =-
+C= =- 
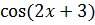 +C
+C
Пример 3:
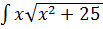 dx= (положим t= x2 +25, тогда dt = 2x dx, x dx=
dx= (положим t= x2 +25, тогда dt = 2x dx, x dx= 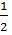 dt) =
dt) = 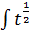 *
*  dt=
dt= 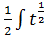 dt=
dt= 
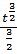 +C =
+C = 
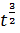 +C =
+C = 
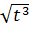 +C =
+C = 
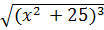 +C
+C
Определенный интеграл.
Если существует определенный интеграл от функции f(x) , то в этом случае функция называется интегрируемой на отрезке 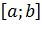 .
.
Для интегрируемости функции на отрезке 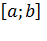 достаточно, чтобы она была непрерывна на нем или имела конечное число точек конечных разрывов.
достаточно, чтобы она была непрерывна на нем или имела конечное число точек конечных разрывов.
Если функция непрерывна на 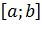 , то от нее существует неопределенный интеграл
, то от нее существует неопределенный интеграл
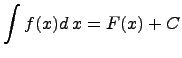
и имеет место формула
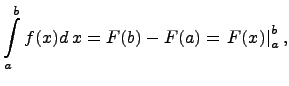
т.е. определенный интеграл от непрерывной функции равен разности значений первообразной функции (или неопределенного интеграла) при верхнем и нижнем пределах.
Формула
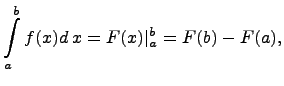
называется формулой Ньютона-Лейбница.
Пример 1:
Необходимо найти определенный интеграл
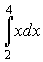
Имеем:
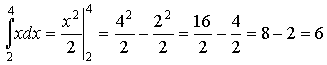
Таким образом искомый интеграл равен 6.
Пример 2:
Вычислить интеграл: 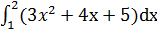
Решение:
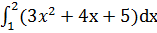 =( 3
=( 3 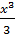 + 4
+ 4 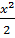 +5x)
+5x) 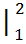 =
= 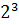 +2
+2 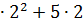 -
-
- ( 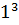 +2
+2 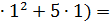 26- 8=18.
26- 8=18.
Приложение определенного интеграла в экономике
Интегральное исчисление дает богатый математический аппарат для моделирования и исследования процессов, происходящих в экономике.
Задача . Известно, что спрос на некоторый товар задается функцией p = 4 – q2, где q – количество товара (в шт.), p – цена единицы товара (в руб.), а равновесие на рынке данного товара достигается при p* = q* = 1. Определите величину потребительского излишка.
Решение.
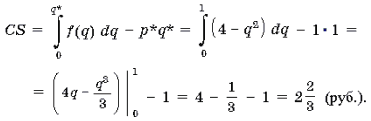
Сложение комплексных чисел
Пример 1:
Сложить два комплексных числа 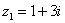 ,
, 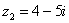
Для того чтобы сложить два комплексных числа нужно сложить их действительные и мнимые части:
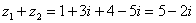
Действие настолько очевидно, что не нуждается в дополнительных комментариях.
Таким нехитрым способом можно найти сумму любого количества слагаемых: просуммировать действительные части и просуммировать мнимые части.
Для комплексных чисел справедливо правило первого класса: 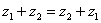 – от перестановки слагаемых сумма не меняется.
– от перестановки слагаемых сумма не меняется.
Вычитание комплексных чисел
Пример 2:
Найти разности комплексных чисел 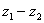 и
и 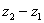 , если
, если 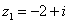
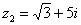
Действие аналогично сложению, единственная особенность состоит в том, что вычитаемое нужно взять в скобки, а затем – стандартно раскрыть эти скобки со сменой знака:
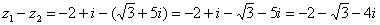
Результат не должен смущать, у полученного числа две, а не три части. Просто действительная часть – составная: 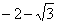 . Для наглядности ответ можно переписать так:
. Для наглядности ответ можно переписать так: 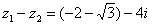 .
.
Рассчитаем вторую разность:
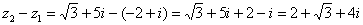
Здесь действительная часть тоже составная: 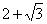
Чтобы не было какой-то недосказанности, приведу короткий пример с «нехорошей» мнимой частью: 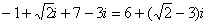 . Вот здесь без скобок уже не обойтись.
. Вот здесь без скобок уже не обойтись.
Умножение комплексных чисел
Настал момент познакомить вас со знаменитым равенством:
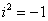
Пример 3:
Найти произведение комплексных чисел 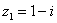 ,
, 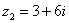
Очевидно, что произведение следует записать так:
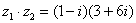
Что напрашивается? Напрашивается раскрыть скобки по правилу умножения многочленов. Так и нужно сделать! Все алгебраические действия вам знакомы, главное, помнить, что 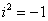 и быть внимательным.
и быть внимательным.
Повторим школьное правило умножения многочленов: Чтобы умножить многочлен на многочлен нужно каждый член одного многочлена умножить на каждый член другого многочлена.
Я распишу подробно:
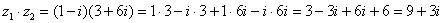
Надеюсь, всем было понятно, что 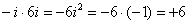
Внимание, и еще раз внимание, чаще всего ошибку допускают в знаках.
Как и сумма, произведение комплексных чисел перестановочно, то есть справедливо равенство: 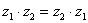 .
.
Деление комплексных чисел
Пример 4:
Даны комплексные числа 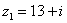 ,
, 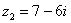 . Найти частное
. Найти частное 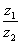 .
.
Составим частное:

Деление чисел осуществляется методом умножения знаменателя и числителя на сопряженное знаменателю выражение.
Вспоминаем формулу 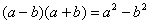 и смотрим на наш знаменатель:
и смотрим на наш знаменатель: 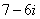 . В знаменателе уже есть
. В знаменателе уже есть 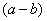 , поэтому сопряженным выражением в данном случае является
, поэтому сопряженным выражением в данном случае является 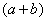 , то есть
, то есть 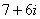
Согласно правилу, знаменатель нужно умножить на 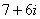 , и, чтобы ничего не изменилось, домножить числитель на то же самое число
, и, чтобы ничего не изменилось, домножить числитель на то же самое число 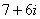 :
:
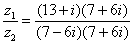
Далее в числителе нужно раскрыть скобки (перемножить два числа по правилу, рассмотренному в предыдущем пункте). А в знаменателе воспользоваться формулой 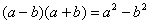 (помним, что
(помним, что 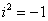 и не путаемся в знаках!!!).
и не путаемся в знаках!!!).
Распишу подробно:
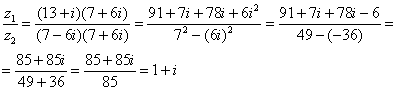
Пример подобран «хороший», если взять два произвольных числа, то в результате деления почти всегда получатся дроби, что-нибудь вроде 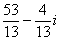 .
.
Решение.
Количество всех элементарных исходов равно 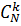 . Для подсчета числа благоприятных случаев рассуждаем так: из n бракованных можно выбрать s деталей
. Для подсчета числа благоприятных случаев рассуждаем так: из n бракованных можно выбрать s деталей 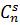 способами, а из N – n небракованных можно выбрать k – s небракованных деталей
способами, а из N – n небракованных можно выбрать k – s небракованных деталей 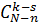 способами; по правилу произведения число благоприятных случаев равно
способами; по правилу произведения число благоприятных случаев равно 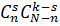 . Искомая вероятность равна:
. Искомая вероятность равна:
p = 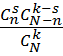 (1)
(1)
Замечание:
Всякое k-членное подмножество n-членного множества называется сочетанием из n элементов по k.
Число различных сочетаний из n элементов по k обозначается 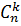 .
.
Справедлива формула
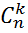 =
= 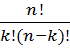 , (2)
, (2)
n! =1 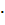 2
2 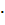 3
3 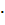 4
4 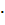 …
…  n
n
Пример 2:
В партии из 12 деталей имеется 7 стандартных. Найти вероятность того, что среди шести взятых наугад деталей 4 стандартных.
Решение.
Искомую вероятность найдем по формуле (1) для случая
N =12, n =7, k = 6, s = 4.
p = 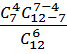 =
= 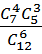 =
= 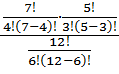 =
= 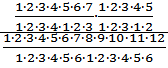
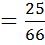 .
.
ЗАДАНИЯ КОНТРОЛЬНОЙ РАБОТЫ
Задание №1.
| Номер варианта | Задание: Найти произведение матриц АВ = С, если А, В даны: |
| 1 | А = 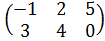 , В = , В = 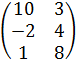
|
| 2 | А = 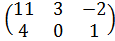 , В = , В = 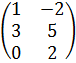
|
| 3 | А = 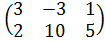 , В = , В = 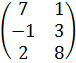
|
| 4 | А = 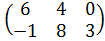 , В = , В = 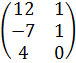
|
| 5 | А = 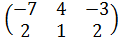 , В = , В = 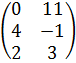
|
| 6 | А = 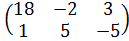 , В = , В = 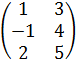
|
| 7 | А = 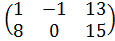 , В = , В = 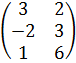
|
| 8 | А = 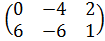 , В = , В = 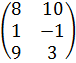
|
| 9 | А = 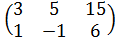 , В = , В = 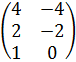
|
| 10 | А = 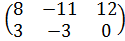 , В = , В = 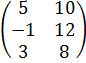
|
Задание №2.
| Номер варианта | Задание: Для множеств А и В найти: АUВ; А∩В; АΔВ; А\В; А×В; А×А; В2 . |
| 1 | А = 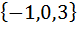 , В = , В = 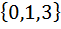
|
| 2 | А = 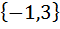 , В = , В = 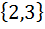
|
| 3 | А = 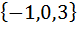 , В = , В = 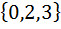
|
| 4 | А = 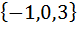 , В = , В = 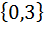
|
| 5 | А = 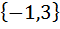 , В = , В = 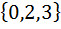
|
| 6 | А = 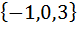 , В = , В = 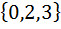
|
| 7 | А = 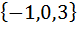 , В = , В = 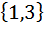
|
| 8 | А = 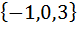 , В = , В = 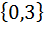
|
| 9 | А = 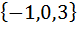 , В = , В = 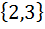
|
| 10 | А = 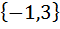 , В = , В = 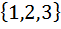
|
Задание №3.
| Номер варианта | Задание: Выполнить действия | |||
| 1 | (1+3i)+(-3+i) | (5-3i)×(2-5i) | (5+4i)-(-3+4i) | (2+3i)/(2-3i) |
| 2 | (-4+3i)+(4-3i) | (3+5i)×(2+3i) | (4+2i)-(-1+2i) | (5-4i)/(-3+2i) |
| 3 | (-2+5i)+(2-5i) | (3-4i)×( -7+3i) | (7-2i)-( -4+3i) | (-5+2i)/(6-7i) |
| 4 | (3-4i)+(-3+4i) | (6+7i)×(-5+2i) | (-9+4i)-( 3+5i) | (1+8i)/( -3+i) |
| 5 | (7-2i)+(-7+3i) | (1+8i)×(-9+4i) | (2+3i)-(-3+i) | (-8+i)/(7-2i) |
| 6 | (-5+2i)+(5-2i) | (3+4i)×( -8+i) | (-3+4i)-(6+7i) | (6-7i)/( -1+2i) |
| 7 | (-6+7i)+(6-7i) | (7-2i)×( -3+i) | (3+5i)-(-9+4i) | (3+4i)/( -5+2i) |
| 8 | (1+8i)+(-8+i) | (2+3i)×(6-7i) | (-5+2i)-(3+4i) | (-9+4i)/(5-7i) |
| 9 | (-9+4i)+(9-4i) | (-5+2i)×( 7-2i) | (-4+3i)-( 2+3i) | (6+7i)/( 1+8i) |
| 10 | (8-5i)+(-8+5i) | (-1+2i)×(6+7i) | (7-5i)-(-8+i) | (3+5i)/(-4+3i) |
З ада ние №4.
| № варианта | Задание: Исследовать свойства функции и построить её график |
| 1 | y = 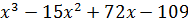
|
| 2 | y = 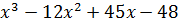
|
| 3 | y = 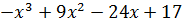
|
| 4 | y = 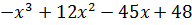
|
| 5 | y = 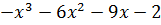
|
| 6 | y = 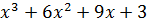
|
| 7 | y = 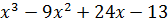
|
| 8 | y = 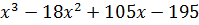
|
| 9 | y = 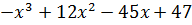
|
| 10 | y = 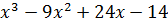
|
Задание №5.
| Номер варианта | Задание: Найти интегралы | ||
| 1 | 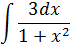
| 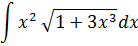
| 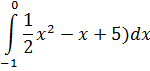
|
| 2 | 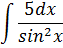
| 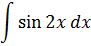
| 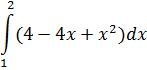
|
| 3 | 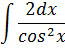
| 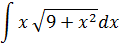
| 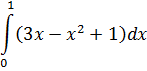
|
| 4 | 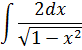
| 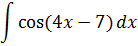
| 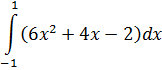
|
| 5 | 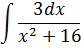
| 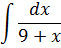
| 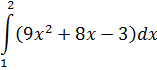
|
| 6 | 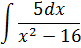
| 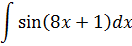
| 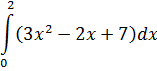
|
| 7 | 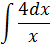
| 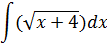
| 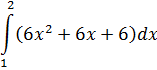
|
| 8 | 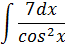
| 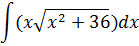
| 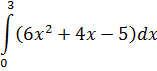
|
| 9 | 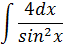
| 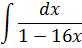
| 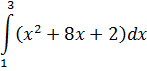
|
| 10 | 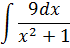
| 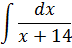
| 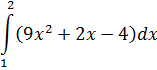
|
Задание №6.
| Номер варианта | Задание: Решить задачу |
| 1 | В партии из 8 деталей имеется 6 стандартных. Найти вероятность того, что среди пяти взятых наугад деталей ровно три стандартных. |
| 2 | В цехе работают 6 мужчин и 4 женщины. По табельным номерам наудачу отобраны 7 человек. Найти вероятность того, что среди отобранных лиц окажутся 3 женщины. |
| 3 | В группе 12 студентов, среди которых 8 отличников. По списку отобраны 9 студентов. Найти вероятность того, что среди отобранных студентов пять отличников. |
| 4 | В урне 5 белых и 4 черных шаров. Из урны наугад вынимают 3 шара. Найти вероятность того, что среди вынутых шаров будет 2 белых. |
| 5 | В партии из 10 деталей имеется 8 стандартных. Найти вероятность того, что среди 6 взятых наугад деталей ровно 4 стандартных. |
| 6 | В группе 16 студентов, среди которых 10 отличников. По списку отобраны 12 студентов. Найти вероятность того, что среди отобранных студентов 6 отличников |
| 7 | В цехе работают 7 мужчин и 5 женщин. По табельным номерам наудачу отобраны 8 человек. Найти вероятность того, что среди отобранных лиц окажутся 4 женщины. |
| 8 | В урне 7 белых и 5 черных шаров. Из урны наугад вынимают 6 шаров. Найти вероятность того, что среди вынутых шаров будет 4 белых. |
| 9 | В партии из 12 деталей имеется 8 стандартных. Найти вероятность того, что среди 7 взятых наугад деталей ровно 5 стандартных. |
| 10 | В группе 14 студентов, среди которых 9 отличников. По списку отобраны 11 студентов. Найти вероятность того, что среди отобранных студентов 5 отличников |
КОНТРОЛЬНАЯ РАБОТА
по дисциплине:
« Математика »
Курс 1 Шифр _______
Выполнил Ф.И.О. .
Специальность ________________
Дата _______________
Преподаватель:
Лиховидова Е.Н.
Сергиев Посад
2017
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
ПО ВЫПОЛНЕНИЮ
ДОМАШНЕЙ КОНТРОЛЬНОЙ РАБОТЫ
по учебной дисциплине:
«Математика»
для студентов заочной формы обучения
специальности 35.02.08 Электрификация и автоматизация сельского хозяйства
(на базе среднего общего образования)
Преподаватель: Лиховидова Елена Николаевна
Сергиев Посад
2017г
Данное методическое пособие содержит общие рекомендации по выполнению контрольной работы, краткие теоретические сведения, необходимые для выполнения контрольной работы, образцы решения задач, приведены примеры использования математических методов при решении задач, контрольные задания.
ПРИМЕРНЫЙ ТЕМАТИЧЕСКИЙ ПЛАН
Дата: 2018-11-18, просмотров: 785.