Матрица – это прямоугольная таблица каких-либо элементов. В качестве элементов мы будем рассматривать числа, то есть числовые матрицы. ЭЛЕМЕНТ – это термин. Термин желательно запомнить, он будет часто встречаться, не случайно я использовал для его выделения жирный шрифт.
Обозначение: матрицы обычно обозначают прописными латинскими буквами 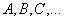
Пример: рассмотрим матрицу «два на три»:
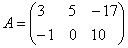
Данная матрица состоит из шести элементов:
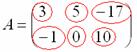
Все числа (элементы) внутри матрицы существуют сами по себе, то есть ни о каком вычитании речи не идет:
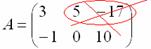
Это просто таблица (набор) чисел!
Рассматриваемая матрица имеет две строки:
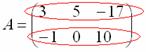
и три столбца:

СТАНДАРТ: когда говорят о размерах матрицы, то сначала указывают количество строк, а только потом – количество столбцов. Мы только что разобрали матрицу «два на три».
Если количество строк и столбцов матрицы совпадает, то матрицу называют квадратной, например: 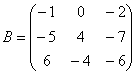 – матрица «три на три».
– матрица «три на три».
Если в матрице один столбец 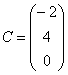 или одна строка
или одна строка 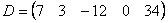 , то такие матрицы также называют векторами.
, то такие матрицы также называют векторами.
Действия с матрицами:
Умножение матрицы на число.
Пример:
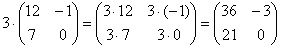
Для того чтобы умножить матрицу на число, нужно каждый элемент матрицы умножить на данное число. В данном случае – на тройку.
Сумма (разность) матриц.
Сумма матриц действие несложное.
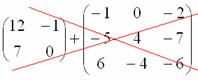
НЕ ВСЕ МАТРИЦЫ МОЖНО СКЛАДЫВАТЬ. Для выполнения сложения (вычитания) матриц, необходимо, чтобы они были ОДИНАКОВЫМИ ПО РАЗМЕРУ.
Например, если дана матрица «два на два», то ее можно складывать только с матрицей «два на два» и никакой другой!
Пример:
Сложить матрицы 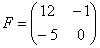 и
и 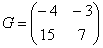
Для того чтобы сложить матрицы, необходимо сложить их соответствующие элементы:
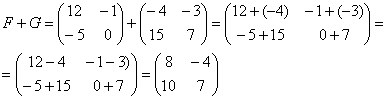
Для разности матриц правило аналогичное, необходимо найти разность соответствующих элементов.
Пример:
Найти разность матриц 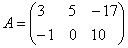 ,
, 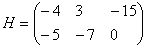
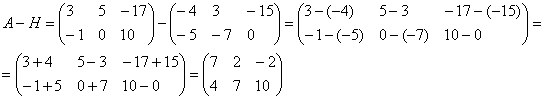
Умножение матриц.
Какие матрицы можно умножать?
Чтобы матрицу  можно было умножить на матрицу
можно было умножить на матрицу  необходимо, чтобы число столбцов матрицы
необходимо, чтобы число столбцов матрицы  равнялось числу строк матрицы
равнялось числу строк матрицы  .
.
Пример:
Можно ли умножить матрицу 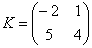 на матрицу
на матрицу 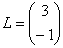 ?
?

 , значит, умножать данные матрицы можно.
, значит, умножать данные матрицы можно.
А вот если матрицы переставить местами, то, в данном случае, умножение уже невозможно!

 , следовательно, выполнить умножение невозможно, и вообще, такая запись не имеет смысла
, следовательно, выполнить умножение невозможно, и вообще, такая запись не имеет смысла

Следует отметить, что в ряде случаев можно умножать матрицы и так, и так.
Например, для матриц, 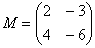 и
и 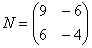 возможно как умножение
возможно как умножение  , так и умножение
, так и умножение 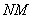
Как умножить матрицы?
Начнем с самого простого:
Пример:
Умножить матрицу 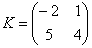 на матрицу
на матрицу 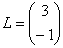
Сразу привожу формулу для каждого случая:
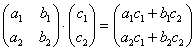 – попытайтесь сразу уловить закономерность.
– попытайтесь сразу уловить закономерность.
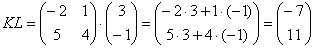
Пример сложнее:
Умножить матрицу 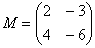 на матрицу
на матрицу 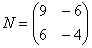
Формула: 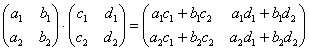
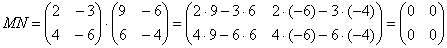
В результате получена так называемая нулевая матрица.
Попробуйте самостоятельно выполнить умножение 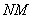 (правильный ответ
(правильный ответ 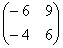 ).
).
Обратите внимание, что 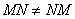 ! Таким образом, переставлять матрицы в произведении нельзя!
! Таким образом, переставлять матрицы в произведении нельзя!
Если в задании предложено умножить матрицу 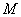 на матрицу
на матрицу 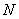 , то и умножать нужно именно в таком порядке. Ни в коем случае не наоборот.
, то и умножать нужно именно в таком порядке. Ни в коем случае не наоборот.
Переходим к матрицам третьего порядка:
Умножить матрицу 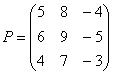 на матрицу
на матрицу 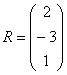
Формула очень похожа на предыдущие формулы:
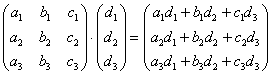
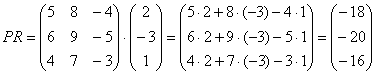
А теперь попробуйте самостоятельно разобраться в умножении следующих матриц:
Умножьте матрицу 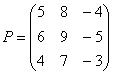 на матрицу
на матрицу 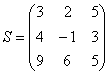
Вот готовое решение, но постарайтесь сначала в него не заглядывать!
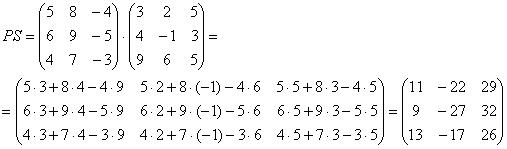
Дата: 2018-11-18, просмотров: 870.