1. Найти область определения функции. Выделить особые точки (точки разрыва).
2. Проверить наличие вертикальных асимптот в точках разрыва и на границах области определения.
3. Найти точки пересечения с осями координат
4. Установить, является ли функция чётной или нечётной.
5. Определить, является ли функция периодической или нет (только для тригонометрических функций, остальные непериодические, пункт пропускается).
6. Найти точки экстремума и интервалы монотонности (возрастания и убывания) функции.
7. Найти точки перегиба и интервалы выпуклости-вогнутости.
8. Найти наклонные асимптоты функции.
9. Построить график функции.
Пример:
Исследовать функцию методами дифференциального исчисления и построить график y = x 3 +6 x 2 +9 x +2
РЕШЕНИЕ:
1) Область определения функции – вся числовая прямая, то есть
D (y) = (−∞; +∞) .
Точек разрыва нет, вертикальных асимптот нет.
2) Точки пересечения с осями координат:
Ox : найти затруднительно
Oy:x=0⇒ 03 +6*02 +9*0+2=2 ⇒ Точка (0;2)
3)Функция общего вида, так как
y(-x) = -x3 +6x2 -9x+2≠ ±y(x)
4) Экстремумы и монотонность. Вычисляем первую производную:
y'=3x2 +12x+9
Находим критические точки: y'=0; 3x2 +12x+9=0; x1 =-1; x2 =-3.
Исследуем знак производной на интервалах,
на которые критические точки делят область определения функции.
y' + - +
 |
y -3 -1 x
Функция возрастает на интервалах (−∞ ;-3),(-1; +∞) , убывает на интервале
(-3;-1). Функция имеет минимум в точке x = -1 , y(-1) =-2 , функция имеет максимум в точке x = -3 , y(-3)=2.
5) Выпуклость и точки перегиба. Вычисляем вторую производную.
y''=(3x2 +12x+9)'=6x+12
Находим критические точки: y''=0; 6x+12=0; x=-2.
Исследуем знак производной на интервалах, на
которые критические точки делят область определения функции.
y'' - +




y -2 x
Функция выпукла вверх на интервале (−∞;-2) , выпукла вниз на интервале
(-2 ; +∞) . Точка перегиба: x =-2, y(-2) = 0.
6) Асимптоты.
Так как  =
=  =∞ , асимптот нет.
=∞ , асимптот нет.
7) Строим график функции.

| |
|


Интегральное исчисление.
| 1.Основные правила интегрирования |
1. Если 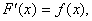 то то 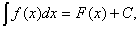 где где 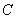 – произвольная постоянная.
2. – произвольная постоянная.
2. 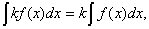 где где 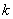 – постоянная.
3. – постоянная.
3. 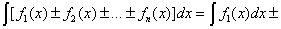
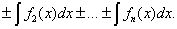
|
| 2.Таблица основных неопределенных интегралов |
1. 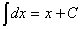 .
2. .
2. 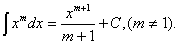 3.
3. 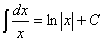 .
4. .
4. 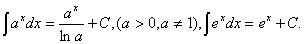 5.
5. 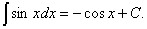 6.
6. 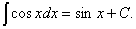 7.
7. 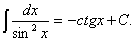 8.
8. 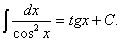 9.
9. 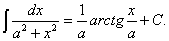 10.
10. 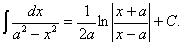 11.
11. 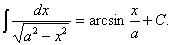 12.
12. 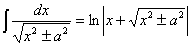 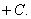
|
| 3.Непосредственное интегрирование |
Отыскание неопределенного интеграла с помощью таблицы, правил и тождественных преобразований называют непосредственным интегрированием.
Пример:
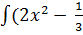 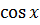 - - 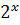 + + 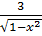 )dx = 2 )dx = 2 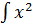 dx - dx -  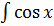 dx - dx - 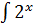 dx + 3 dx + 3 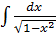 = 2 = 2 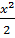 - -  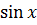 +3 arcsin x + C
При интегрировании использованы правила 2 и 3, а также табличные формулы 2,4,6,11. +3 arcsin x + C
При интегрировании использованы правила 2 и 3, а также табличные формулы 2,4,6,11.
|
| 4.Метод подстановки (замена переменной интегрирования) |
Замена переменной в неопределенном интеграле производится с помощью подстановок двух видов: а) 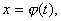 где где 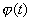 – монотонная, дифференцируемая функция; б) – монотонная, дифференцируемая функция; б) 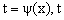 – новая переменная.
В первом случае формула замены переменной имеет вид: – новая переменная.
В первом случае формула замены переменной имеет вид:
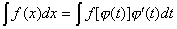 . (1)
Во втором случае: . (1)
Во втором случае:
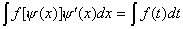 . (2)
В обоих случаях после интегрирования следует возвращаться к старой переменной обратной подстановкой.
Пример 1.
Вычислить интеграл: . (2)
В обоих случаях после интегрирования следует возвращаться к старой переменной обратной подстановкой.
Пример 1.
Вычислить интеграл:
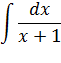 Решение.
Сделаем замену переменных t = x +1 и найдем дифференциал от обеих частей, тогда
dt = (x+1)'dx ⇒ dt= dx
Подставляя все в исходный интеграл, получим:
Решение.
Сделаем замену переменных t = x +1 и найдем дифференциал от обеих частей, тогда
dt = (x+1)'dx ⇒ dt= dx
Подставляя все в исходный интеграл, получим:
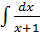 = = 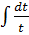 = = 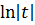 +C = +C = 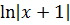 +C,
где C - const . Здесь заключительное действие - это обратная замена переменных.
В данном случае с помощью замены в интеграле удалось свести интеграл к табличному, затем была произведена обратная замена переменных и получен ответ. +C,
где C - const . Здесь заключительное действие - это обратная замена переменных.
В данном случае с помощью замены в интеграле удалось свести интеграл к табличному, затем была произведена обратная замена переменных и получен ответ.
|
Пример 2:
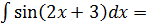 (положим t = 2x+3, тогда x=
(положим t = 2x+3, тогда x=  t-
t-  , dx =
, dx =  dt)
dt)
= 
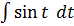 =-
=- 
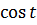 +C= =-
+C= =- 
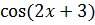 +C
+C
Пример 3:
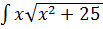 dx= (положим t= x2 +25, тогда dt = 2x dx, x dx=
dx= (положим t= x2 +25, тогда dt = 2x dx, x dx= 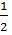 dt) =
dt) = 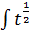 *
*  dt=
dt= 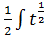 dt=
dt= 
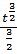 +C =
+C = 
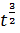 +C =
+C = 
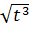 +C =
+C = 
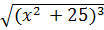 +C
+C
Определенный интеграл.
Если существует определенный интеграл от функции f(x) , то в этом случае функция называется интегрируемой на отрезке 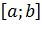 .
.
Для интегрируемости функции на отрезке 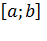 достаточно, чтобы она была непрерывна на нем или имела конечное число точек конечных разрывов.
достаточно, чтобы она была непрерывна на нем или имела конечное число точек конечных разрывов.
Если функция непрерывна на 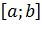 , то от нее существует неопределенный интеграл
, то от нее существует неопределенный интеграл
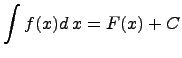
и имеет место формула
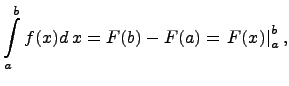
т.е. определенный интеграл от непрерывной функции равен разности значений первообразной функции (или неопределенного интеграла) при верхнем и нижнем пределах.
Формула
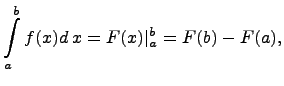
называется формулой Ньютона-Лейбница.
Пример 1:
Необходимо найти определенный интеграл
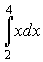
Имеем:
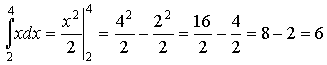
Таким образом искомый интеграл равен 6.
Пример 2:
Вычислить интеграл: 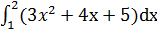
Решение:
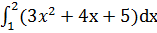 =( 3
=( 3 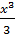 + 4
+ 4 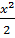 +5x)
+5x) 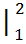 =
= 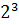 +2
+2 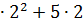 -
-
- ( 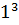 +2
+2 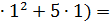 26- 8=18.
26- 8=18.
Приложение определенного интеграла в экономике
Интегральное исчисление дает богатый математический аппарат для моделирования и исследования процессов, происходящих в экономике.
Задача . Известно, что спрос на некоторый товар задается функцией p = 4 – q2, где q – количество товара (в шт.), p – цена единицы товара (в руб.), а равновесие на рынке данного товара достигается при p* = q* = 1. Определите величину потребительского излишка.
Решение.
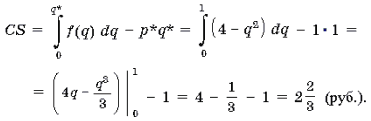
Дата: 2018-11-18, просмотров: 861.