Вариант 8

1. Вероятность того, что год будет урожайным – 0.8. Какова вероятность того, что из пяти рассматриваемых лет более двух неурожайных?
2. Вероятность получить телефонный разговор в течение получаса равна 0.7. Какова вероятность того, что из 4 абонентов больше получаса будут ожидать разговор 2?
3. Вероятность изготовления бракованного генератора равна 0.001.Найти вероятность того,что из 3000 генераторов окажется: а)2 бракованных;б)не более 2 бракованных.
4. Для покупки билета пассажир может обратиться в одну из трех касс. Вероятность обращения в каждую из них зависит от их местоположения и равна соответственно 0.1, 0.5, 0.4. Вероятности того, что к моменту прихода пассажира билеты на нужный рейс будут распроданы, равны 0.7, 0.8, 0.5 соответственно. Пассажир купил билет. Какова вероятность того, что он обратился в кассу с номером 1?
5. Производится испытание трех изделий на надежность. Вероятности выдержать испытания для каждого, соответственно, равны 0.7, 0.8, 0.9. Построить ряд распределения случайной величины Х – числа изделий, выдержавших испытания. Найти М(Х), D(X).
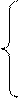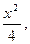6. Случайная величина Х задана функцией распределения F(x). Требуется: а) найти функцию плотности f(x); б) найти M(X) и D(X); в) построить графики F(x) и f(x).                       0, при х < 0;                                                                                                               F(x)=    при 0 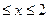;                                                                                                                                                  1, при x > 2.

Контрольная работа по теории вероятностей

Вариант 9

1. Вероятность простоя станка равна 0.2. Найти вероятность того, что из трех проверенных станков два работают.
2. Вероятность того, что покупателю понадобится пальто 48-го размера равна 0.6. Какова вероятность того, что из 10 покупателей не более двоих спросят пальто 48-го размера.
3. Вероятность того, что при упаковке люстра будет повреждена, равна 0.2. Найти вероятность того, что после упаковки 100 люстр поврежденными окажутся: а) 30 штук; б) не более 30 штук.
4. При попадании снаряда в первый отсек самолет сбивается с вероятностью 0.15, во второй – с вероятностью 0.6. Попадания в каждый отсек равновероятны. Самолет сбит одним выстрелом. Какова вероятность, что попали в первый отсек?
5. В мастерской работают три мотора. При существующем режиме работы вероятность того, что мотор в данный момент работает с полной нагрузкой, равна 0.8. Построить ряд распределения случайной величины Х – числа работающих с полной нагрузкой моторов. Найти М(Х), D(X).
6. Случайная величина Х задана функцией распределения F(x). Требуется: а) найти функцию плотности f(x); б) найти M(X) и D(X); в) построить графики F(x) и f(x).                      0, при х < -1;                                                                                                               F(x)= , при -1 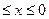;                                                                                                                                                   1, при x > 0.

Контрольная работа по теории вероятностей

Вариант 10

1. Посажены семь семян со всхожестью 60%. Какова вероятность того, что взойдет не менее двух из них?
2. В аквариуме 8 золотых и 3 красных рыбок. Выловили 5 рыбок. Какова вероятность того, что среди них 3 золотых?
3. Вероятность опечатки на странице 0.0025. В книге 800 страниц. Какова вероятность того, что с опечатками будут не более 5 страниц?
4. С поляны ведет три дороги, вероятности выйти по которым из леса равны 0.9, 0.7 и 0.3 соответственно. Чему равна вероятность выйти из леса, если выбор дороги произволен?
5. Рабочий обслуживает три станка. Вероятность того, что в течение часа станок не потребует внимания рабочего, равна для первого станка 0.9, для второго – 0.8, а для третьего – 0.6. Построить ряд распределения случайной величины Х – числа станков, не требующих в течение часа внимания рабочего. Найти М(Х), D(X).
6. Случайная величина Х задана функцией распределения F(x). Требуется: а) найти функцию плотности f(x); б) найти M(X) и D(X); в) построить графики F(x) и f(x).                      0, при х < 0;                                                                                                               F(x)= 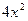 , при 0 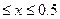;                                                                                                                                               1, при x > 0.5