Контрольная работа по теории вероятностей

(Номер варианта соответствует последней цифре номера зачётки. Если эта цифра – 0, то решается 10 вариант)

Вариант 1

1. Вероятность прижиться для саженца сливы равна 0.6, а для саженца яблони – 0.8. Посадили яблоню и сливу. Найти вероятность того, что из двух посаженных приживется только один саженец.
2. Вероятность того, что арбуз спелый для данной партии равна 0.7. Какова вероятность того, что из 3 купленных арбузов будет 2 спелых?
3. В среднем 30% изготовленных заводом часов спешат. Какова вероятность того, что из 350 часов число часов, которые спешат, окажется: а) равным 100; б) не более 100?
4. По линии передаются два сигнала: А и В с вероятностями 0.7 и 0.3 соответственно. Из-за помех пятая часть сигналов А искажается и принимается как сигнал В, а восьмая часть переданных сигналов В принимается как А. Найти вероятность того, что будет принят сигнал А.
5. В некоторой торговой фирме при перевозке бракуется 5 % товара. Наудачу взяты 3 единицы товара. Построить ряд распределения случайной величины Х – числа единиц брака в выборке. Найти М(Х), D(X).
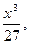6. Случайная величина Х задана функцией распределения F(x). Требуется: а) найти функцию плотности f(x); б) найти M(X) и D(X); в) построить графики F(x) и f(x).                      0, при х < 0;                                                                                                               F(x)=   при 0 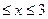;                                                                                                                                                 1, при x > 3.

Контрольная работа по теории вероятностей

Вариант 2

1. Вероятность проиграть в некоторой игре равна 0.5. Найти вероятность того, что из 6 партий не меньше трех будет проиграно.
2. При транспортировке винограда из каждых 100 ящиков в среднем один оказывается испорченным. Найти вероятность того, что из 3 ящиков: а) ни один не будет испорчен; б) не более одного будет испорченным.
3. Вероятность отказа элемента равна 0.001 и не зависит от состояния других элементов. Найти вероятность того, что из 10000 элементов откажут: а) два элемента; б) не менее двух элементов.
4. Число легковых машин, проезжающих по шоссе возле бензоколонки относится к числу грузовых машин как 3:4. Вероятность того, что будет заправляться грузовая машина, равна 0.1, легковая – 0.2. Для заправки подъехала машина. Какова вероятность, что это грузовая?
5. Два стрелка стреляют каждый по своей мишени, делая независимо друг от друга по одному выстрелу. Вероятность попадания для первого стрелка равна 0.6, для второго – 0.7. Построить ряд распределения случайной величины Х – разности числа попаданий первым стрелком и вторым. Найти М(Х), D(X).
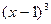6. Случайная величина Х задана функцией распределения F(x). Требуется: а) найти функцию плотности f(x); б) найти M(X) и D(X); в) построить графики F(x) и f(x).                      0, при х < 1;                                                                                                               F(x)=   при 1 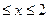;                                                                                                                                                   1, при x > 2.

Контрольная работа по теории вероятностей

Вариант 3

1. Вероятность ровно одного попадания в цель при залпе из двух орудий равна 0.38. Найти вероятность поражения цели при одном выстреле вторым орудием, если для первого орудия эта вероятность равна 0.7.
2. В лотерее выпущено 100 билетов. Выигрыш падает на 10 билетов. Какова вероятность, что из трех билетов хоть один выигрышный?
3. Среди семян имеется 0.2% сорняков. Какова вероятность того, что из 5000 семян окажется не менее 5 сорняков?
4. В группе учатся 5 отличников, 6 хорошистов, 7 троечников и два студента не успевают. Вероятность правильного ответа на вопрос отличника – 0.9, хорошиста – 0.7, троечника – 0.5, неуспевающего – 0.2. Найти вероятность того, что студент, правильно ответивший на вопрос, является хорошистом.
5. Производятся испытания трех изделий на надежность, причем, вероятность выдержать испытания для каждого равна 0.8. Построить ряд распределения случайной величины Х – числа изделий, выдержавших испытания. Найти М(Х), D(X).
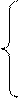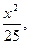6. Случайная величина Х задана функцией распределения F(x). Требуется: а) найти функцию плотности f(x); б) найти M(X) и D(X); в) построить графики F(x) и f(x).                       0, при х < 0;                                                                                                   F(x)=    при 0 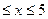;                                                                                                                                                           1, при x > 5.

Вариант 4

1. Вероятность того, что автомат по продаже газет сработает при бросании монеты, равна 0.9. Найти вероятность того, что при двух бросаниях монет автомат сработает только один раз.
2. Вероятность того, что лампа перегорит равна 0.2. Найти вероятность того, что из 7 ламп: а) перегорят две лампы; б) хотя бы две лампы перегорят.
3. На каждую тысячу букв текста русского языка в среднем приходится 110 букв «О». Какова вероятность того, что из 2000 букв в тексте буква «О» встретится от 200 до 250 раз?
4. Стоящие в пирамиде 10 карабинов составляют 4 группы, различающиеся по своим боевым качествам. В первой группе - 2 карабина, во второй – 4, в третьей – 3, в четвертой – 1 карабин. Вероятность попадания в мишень для данного стрелка из карабина 1-й группы – 0.9, второй – 0.8, третьей – 0.7, четвертой – 0.6. Стрелок берет карабин наугад и стреляет. Какова вероятность того, что мишень не будет поражена?
5. Игральную кость бросили 3 раза. Построить ряд распределения случайной величины Х – числа выпадения двух очков. Найти М(Х), D(X).
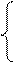6. Случайная величина Х задана функцией распределения F(x). Требуется: а) найти функцию плотности f(x); б) найти M(X) и D(X); в) построить графики F(x) и f(x).                      0, при х < 0;                                                                                                               F(x)= 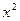, при 0 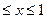;                                                                                                                                                  1, при x > 1.

Вариант 5

1. Студент может получить “пятерку” на экзамене по философии с вероятностью 0.5, а по математике – с вероятностью p. Определить p, если вероятность того, что студент получит “пятерку” хотя бы по одному из названных предметов равна 0.65.
2. Среди 20 пар обуви 16 – первого сорта, а остальные - второго. Какова вероятность того, что из 3 взятых наудачу пар одна будет второго сорта?
3. В зале 700 мест. Считая, что в году 365 дней, найти вероятность того, что в полном зале а) 3 зрителя родились 8 марта; б) не более трех родились в этот же день.
4. Производительность первого станка в три раза больше производительности второго. Вероятность брака для первого станка - 0.02, для второго – 0.03. Найти вероятность того, что взятая наугад деталь стандартна.
5. Имеется 20 лампочек, среди которых 4 дефектных. Наудачу выбраны 3 лампочки для проверки. Построить ряд распределения случайной величины Х – числа дефектных лампочек в выборке. Найти М(Х), D(X).
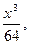6. Случайная величина Х задана функцией распределения F(x). Требуется: а) найти функцию плотности f(x); б) найти M(X) и D(X); в) построить графики F(x) и f(x).                      0, при х < 0;                                                                                                               F(x)=   при 0 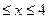;                                                                                                                                                 1, при x > 4.

Вариант 6

1. В среднем 30% часов, выпускаемых некоторым заводом, спешат. Найти вероятность того, что при проверке случайным образом отобранных пяти часов этого завода не более двух будут спешить.
2. Вероятность своевременной починки аппарата – 0.8. Какова вероятность того, что из 10, принятых в ремонт, своевременно будут починены 9 аппаратов?
3. Вероятность пробоя конденсатора во время испытания равна 0.01. Какова вероятность того, что из 100 конденсаторов не выдержат испытания не более трех?
4. Вероятности того, что во время работы ЭВМ произойдет сбой в арифметическом устройстве, в оперативной памяти, в остальных устройствах относятся как 3:2:5. Вероятности обнаружения перечисленных сбоев соответственно равны 0.8, 0.9, 0.7. Найти вероятность того, что возникший в машине сбой будет обнаружен.
5. Опыт состоит из четырех независимых бросаний монеты. Построить ряд распределения случайной величины Х – числа появлений герба. Найти М(Х), D(X).
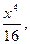6. Случайная величина Х задана функцией распределения F(x). Требуется: а) найти функцию плотности f(x); б) найти M(X) и D(X); в) построить графики F(x) и f(x).                      0, при х < 0;                                                                                                               F(x)=   при 0 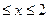;                                                                                                                                                   1, при x > 2.

Вариант 7

1. В среднем восьми из десяти зрителей нравится игра актера А, и пяти из 20 не нравится игра актера В. Некоторого зрителя спросили об игре актеров А и В. Какова вероятность, что ему понравился хотя бы один из них?
2. Из 10 часов 2 требуют чистки. Мастер наугад берет трое часов. Какова вероятность того, что из них: а) ни одни часы не потребуют чистки; б) не более одних часов требуют чистки.
3. Вероятность перерасхода отпущенного кредита равна 0.015 для каждого предприятия. Найти вероятность того, что из 400 предприятий: а) у 395 не будет перерасхода; б) перерасход будет не менее, чем у трех предприятий.
4. У колхоза вероятность получить прибыль в урожайный год равна 0.13, в неурожайный – 0.08. Вероятность урожайного года – 0.8. Какова вероятность получить прибыль в будущем году?
5. Построить ряд распределения случайной величины Х – числа попаданий мячом в корзину при двух бросках, если вероятность попадания при одном броске равна 0.3. Найти М(Х), D(X).
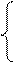6. Случайная величина Х задана функцией распределения F(x). Требуется: а) найти функцию плотности f(x); б) найти M(X) и D(X); в) построить графики F(x) и f(x).                      0, при х < 1;                                                                                                               F(x)=   при 1 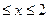;                                                                                                                                                   1, при x > 2.

Вариант 8

1. Вероятность того, что год будет урожайным – 0.8. Какова вероятность того, что из пяти рассматриваемых лет более двух неурожайных?
2. Вероятность получить телефонный разговор в течение получаса равна 0.7. Какова вероятность того, что из 4 абонентов больше получаса будут ожидать разговор 2?
3. Вероятность изготовления бракованного генератора равна 0.001.Найти вероятность того,что из 3000 генераторов окажется: а)2 бракованных;б)не более 2 бракованных.
4. Для покупки билета пассажир может обратиться в одну из трех касс. Вероятность обращения в каждую из них зависит от их местоположения и равна соответственно 0.1, 0.5, 0.4. Вероятности того, что к моменту прихода пассажира билеты на нужный рейс будут распроданы, равны 0.7, 0.8, 0.5 соответственно. Пассажир купил билет. Какова вероятность того, что он обратился в кассу с номером 1?
5. Производится испытание трех изделий на надежность. Вероятности выдержать испытания для каждого, соответственно, равны 0.7, 0.8, 0.9. Построить ряд распределения случайной величины Х – числа изделий, выдержавших испытания. Найти М(Х), D(X).
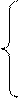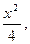6. Случайная величина Х задана функцией распределения F(x). Требуется: а) найти функцию плотности f(x); б) найти M(X) и D(X); в) построить графики F(x) и f(x).                       0, при х < 0;                                                                                                               F(x)=    при 0 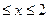;                                                                                                                                                  1, при x > 2.

Вариант 9

1. Вероятность простоя станка равна 0.2. Найти вероятность того, что из трех проверенных станков два работают.
2. Вероятность того, что покупателю понадобится пальто 48-го размера равна 0.6. Какова вероятность того, что из 10 покупателей не более двоих спросят пальто 48-го размера.
3. Вероятность того, что при упаковке люстра будет повреждена, равна 0.2. Найти вероятность того, что после упаковки 100 люстр поврежденными окажутся: а) 30 штук; б) не более 30 штук.
4. При попадании снаряда в первый отсек самолет сбивается с вероятностью 0.15, во второй – с вероятностью 0.6. Попадания в каждый отсек равновероятны. Самолет сбит одним выстрелом. Какова вероятность, что попали в первый отсек?
5. В мастерской работают три мотора. При существующем режиме работы вероятность того, что мотор в данный момент работает с полной нагрузкой, равна 0.8. Построить ряд распределения случайной величины Х – числа работающих с полной нагрузкой моторов. Найти М(Х), D(X).
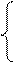6. Случайная величина Х задана функцией распределения F(x). Требуется: а) найти функцию плотности f(x); б) найти M(X) и D(X); в) построить графики F(x) и f(x).                      0, при х < -1;                                                                                                               F(x)= , при -1 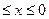;                                                                                                                                                   1, при x > 0.

Вариант 10

1. Посажены семь семян со всхожестью 60%. Какова вероятность того, что взойдет не менее двух из них?
2. В аквариуме 8 золотых и 3 красных рыбок. Выловили 5 рыбок. Какова вероятность того, что среди них 3 золотых?
3. Вероятность опечатки на странице 0.0025. В книге 800 страниц. Какова вероятность того, что с опечатками будут не более 5 страниц?
4. С поляны ведет три дороги, вероятности выйти по которым из леса равны 0.9, 0.7 и 0.3 соответственно. Чему равна вероятность выйти из леса, если выбор дороги произволен?
5. Рабочий обслуживает три станка. Вероятность того, что в течение часа станок не потребует внимания рабочего, равна для первого станка 0.9, для второго – 0.8, а для третьего – 0.6. Построить ряд распределения случайной величины Х – числа станков, не требующих в течение часа внимания рабочего. Найти М(Х), D(X).
6. Случайная величина Х задана функцией распределения F(x). Требуется: а) найти функцию плотности f(x); б) найти M(X) и D(X); в) построить графики F(x) и f(x).                      0, при х < 0;                                                                                                               F(x)= 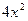 , при 0 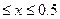;                                                                                                                                               1, при x > 0.5

Контрольная работа по теории вероятностей

(Номер варианта соответствует последней цифре номера зачётки. Если эта цифра – 0, то решается 10 вариант)

Вариант 1

1. Вероятность прижиться для саженца сливы равна 0.6, а для саженца яблони – 0.8. Посадили яблоню и сливу. Найти вероятность того, что из двух посаженных приживется только один саженец.
2. Вероятность того, что арбуз спелый для данной партии равна 0.7. Какова вероятность того, что из 3 купленных арбузов будет 2 спелых?
3. В среднем 30% изготовленных заводом часов спешат. Какова вероятность того, что из 350 часов число часов, которые спешат, окажется: а) равным 100; б) не более 100?
4. По линии передаются два сигнала: А и В с вероятностями 0.7 и 0.3 соответственно. Из-за помех пятая часть сигналов А искажается и принимается как сигнал В, а восьмая часть переданных сигналов В принимается как А. Найти вероятность того, что будет принят сигнал А.
5. В некоторой торговой фирме при перевозке бракуется 5 % товара. Наудачу взяты 3 единицы товара. Построить ряд распределения случайной величины Х – числа единиц брака в выборке. Найти М(Х), D(X).
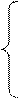6. Случайная величина Х задана функцией распределения F(x). Требуется: а) найти функцию плотности f(x); б) найти M(X) и D(X); в) построить графики F(x) и f(x).                      0, при х < 0;                                                                                                               F(x)= 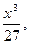  при 0 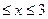;                                                                                                                                                 1, при x > 3.