Вариант 5

1. Студент может получить “пятерку” на экзамене по философии с вероятностью 0.5, а по математике – с вероятностью p. Определить p, если вероятность того, что студент получит “пятерку” хотя бы по одному из названных предметов равна 0.65.
2. Среди 20 пар обуви 16 – первого сорта, а остальные - второго. Какова вероятность того, что из 3 взятых наудачу пар одна будет второго сорта?
3. В зале 700 мест. Считая, что в году 365 дней, найти вероятность того, что в полном зале а) 3 зрителя родились 8 марта; б) не более трех родились в этот же день.
4. Производительность первого станка в три раза больше производительности второго. Вероятность брака для первого станка - 0.02, для второго – 0.03. Найти вероятность того, что взятая наугад деталь стандартна.
5. Имеется 20 лампочек, среди которых 4 дефектных. Наудачу выбраны 3 лампочки для проверки. Построить ряд распределения случайной величины Х – числа дефектных лампочек в выборке. Найти М(Х), D(X).
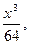6. Случайная величина Х задана функцией распределения F(x). Требуется: а) найти функцию плотности f(x); б) найти M(X) и D(X); в) построить графики F(x) и f(x).                      0, при х < 0;                                                                                                               F(x)=   при 0 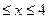;                                                                                                                                                 1, при x > 4.

Контрольная работа по теории вероятностей

Вариант 6

1. В среднем 30% часов, выпускаемых некоторым заводом, спешат. Найти вероятность того, что при проверке случайным образом отобранных пяти часов этого завода не более двух будут спешить.
2. Вероятность своевременной починки аппарата – 0.8. Какова вероятность того, что из 10, принятых в ремонт, своевременно будут починены 9 аппаратов?
3. Вероятность пробоя конденсатора во время испытания равна 0.01. Какова вероятность того, что из 100 конденсаторов не выдержат испытания не более трех?
4. Вероятности того, что во время работы ЭВМ произойдет сбой в арифметическом устройстве, в оперативной памяти, в остальных устройствах относятся как 3:2:5. Вероятности обнаружения перечисленных сбоев соответственно равны 0.8, 0.9, 0.7. Найти вероятность того, что возникший в машине сбой будет обнаружен.
5. Опыт состоит из четырех независимых бросаний монеты. Построить ряд распределения случайной величины Х – числа появлений герба. Найти М(Х), D(X).
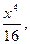6. Случайная величина Х задана функцией распределения F(x). Требуется: а) найти функцию плотности f(x); б) найти M(X) и D(X); в) построить графики F(x) и f(x).                      0, при х < 0;                                                                                                               F(x)=   при 0 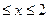;                                                                                                                                                   1, при x > 2.

Контрольная работа по теории вероятностей

Вариант 7

1. В среднем восьми из десяти зрителей нравится игра актера А, и пяти из 20 не нравится игра актера В. Некоторого зрителя спросили об игре актеров А и В. Какова вероятность, что ему понравился хотя бы один из них?
2. Из 10 часов 2 требуют чистки. Мастер наугад берет трое часов. Какова вероятность того, что из них: а) ни одни часы не потребуют чистки; б) не более одних часов требуют чистки.
3. Вероятность перерасхода отпущенного кредита равна 0.015 для каждого предприятия. Найти вероятность того, что из 400 предприятий: а) у 395 не будет перерасхода; б) перерасход будет не менее, чем у трех предприятий.
4. У колхоза вероятность получить прибыль в урожайный год равна 0.13, в неурожайный – 0.08. Вероятность урожайного года – 0.8. Какова вероятность получить прибыль в будущем году?
5. Построить ряд распределения случайной величины Х – числа попаданий мячом в корзину при двух бросках, если вероятность попадания при одном броске равна 0.3. Найти М(Х), D(X).
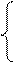6. Случайная величина Х задана функцией распределения F(x). Требуется: а) найти функцию плотности f(x); б) найти M(X) и D(X); в) построить графики F(x) и f(x).                      0, при х < 1;                                                                                                               F(x)=   при 1 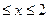;                                                                                                                                                   1, при x > 2.