1 Навіщо необхідно застосовувати перетворення проекційного кресленика?
2 Які ви знаєте способи перетворення кресленика?
3 Суть способу і алгоритм розв’язування задач на обертання навколо осі.
4 Чому вісь обертання вибирають із прямих особливого положення?
5 Скільки перетворень і у якій послідовності необхідно виконати,щоб відрізок із загального положення перевести до положення проекційного?
6 Яким чином треба розташувати нову площину проекцій, щоб площина загального положення стала проекційною?
7 Скільки перетворень і у якій послідовності необхідно виконати, щоб відсік площини із загального положення перевести до положення площини рівня?
ЛЗ-5. Дослідження властивостей багатогранних поверхонь
Мета вивчення теми і виконання графічної роботи:
- набуття вміння будувати креслеників технічних форм і розв’язувати за ними різні інженерно-технічних завдання.
знати: - теоретичні основи побудови креслень;
уміти: - виконувати кресленика простих технічних форм;
- навчитися самостійно працювати над розв’язанням індивідуального завдання.
Література:
[1,с. 140 - 178], [2, с. 35 - 43], [3, с. 50-54]; [4, с. 42 – 48].
Навести відповіді та виконати графічні побудови в робочому зошиті на поставлені запитання
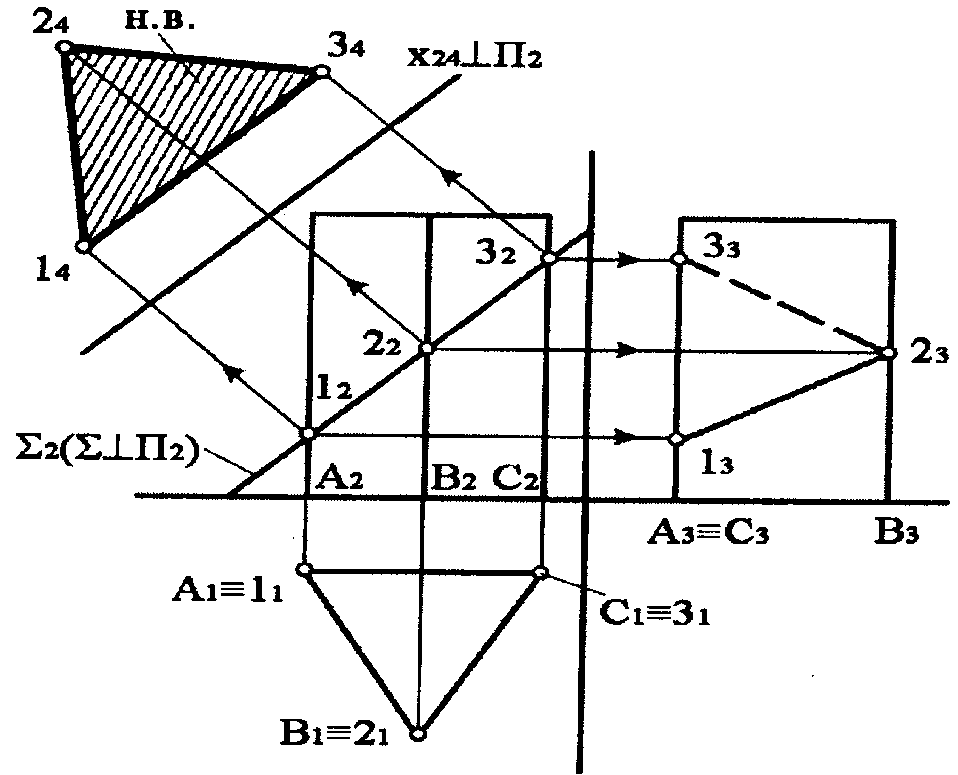
5.1 Дати відповіді на запитання стосовно кресленика, що наведене на рисунку 5.1.
1) Який багатогранник заданий на рисунку?
- На рисунку 5.1 заданий багатогранник, що називається _______
__________________________________________________________________
2) З яких багатокутників складаються грані багатогранника?
- Грані багатогранника складаються з ________________________ .
3) Які положення у просторі займають ребра і грані багатогранника?
- Ребра багатогранника займають ___________________________ положення. Дві грані займають ___________________________ положення, а одна грань ___________________________ положення.
|
| Рисунок 5.1 |
4) Яке положення у просторі займає січна площина S ?
- Січна площина S займає _______________________ положення.
5) По якій фігурі січна площина S перетинає багатогранник і чому?
- Січна площина S перетинає багатогранник по ______________, тому що вона перетинає ____ грані багатогранника.
6) По якому найбільшому багатокутнику може перетинати січна площина заданий багатогранник і яким чином вона повинна бути розташовано відносно заданого багатогранника?
- Січна площина може перетинати заданий багатогранник по
_____________, якщо вона буде розташовано відносно багатогранника таким чином, що перетинатиме ___________________________________ .
7) Яким способом на рисунку 5.1 визначена фігура перерізу багатогранника січною площиною?
- Фігура перерізу багатогранника січною площиною визначена як результат перетину фронтальних проекцій ________________ багатогранника з ____________________ слідом-проекцією січної площини.
8) Яким способом визначена натуральна величина фігури перерізу багатогранника січною площиною?
- Натуральна величина фігури перерізу багатогранника січною площиною визначена способом ___________________________________.
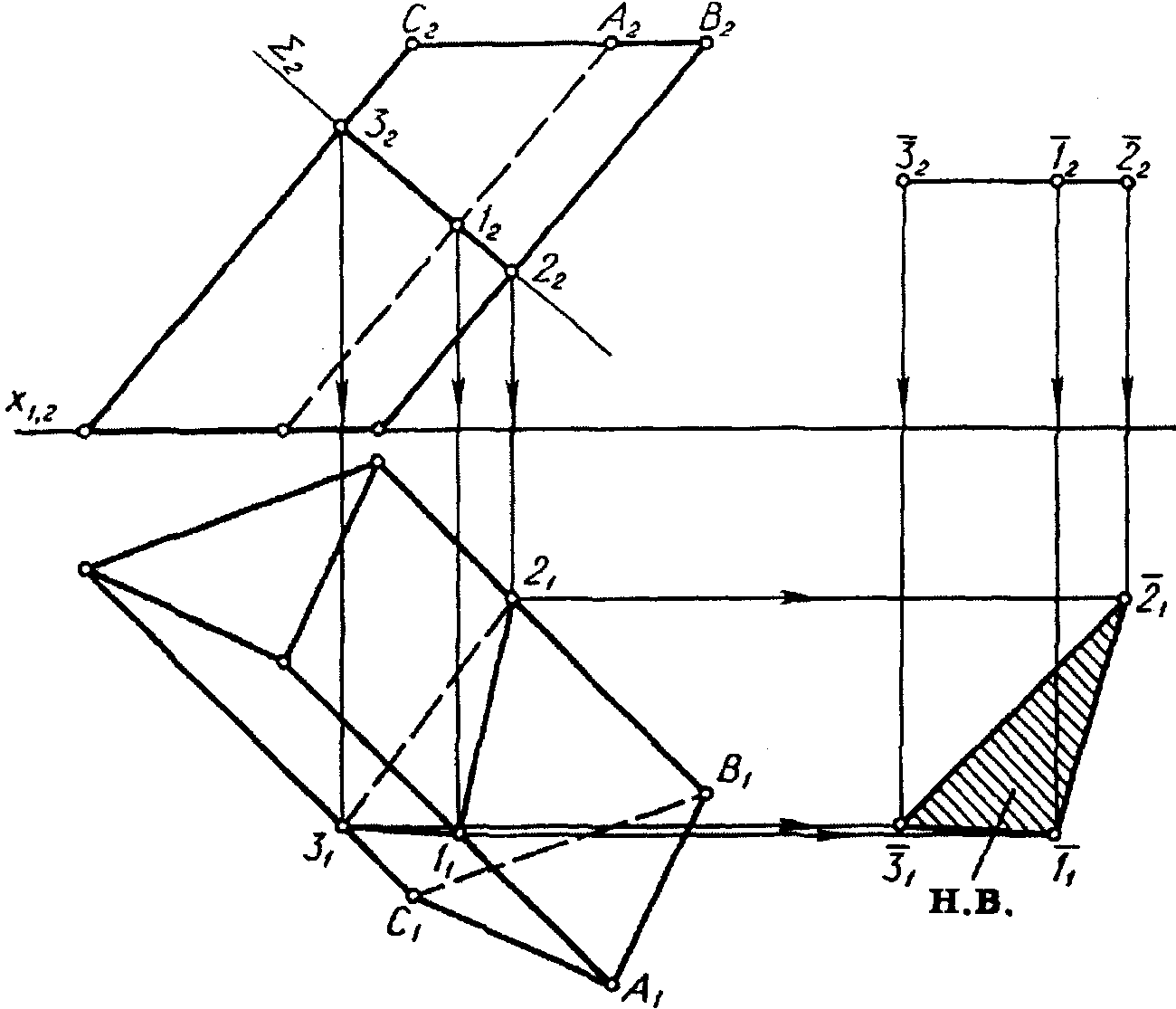
5.2 Дати відповіді на запитання стосовно кресленика, що наведене на рисунку 5.2.
1) Який багатогранник заданий на рисунку?
- На рисунку 5.2 заданий багатогранник, що називається _______
__________________________________________________________________
2) З яких багатокутників складаються грані багатогранника?
- Грані багатогранника складаються з ________________________ .
3) Які положення у просторі займають ребра і грані багатогранника?
- Ребра і грані багатогранника займають ____________________ положення.
4) Яке положення у просторі займає січна площина S ?
- Січна площина S займає _______________________ положення.
5) По якій фігурі січна площина S перетинає багатогранник і чому?
- Січна площина S перетинає багатогранник по ______________, тому що вона перетинає ____ грані багатогранника.
6) Яким способом на рисунку 5.2 визначена фігура перерізу багатогранника січною площиною?
- Фігура перерізу багатогранника січною площиною визначена як результат перетину фронтальних проекцій ________________ багатогранника з ______________________ слідом-проекцією січної площини.
7) Яким способом визначена натуральна величина фігури перерізу багатогранника січною площиною?
- Натуральна величина фігури перерізу багатогранника січною площиною визначена способом ___________________________________ .
|
| Рисунок 5.2- Знаходження натуральної величини перерізу призми методом плоско паралельного переміщення |
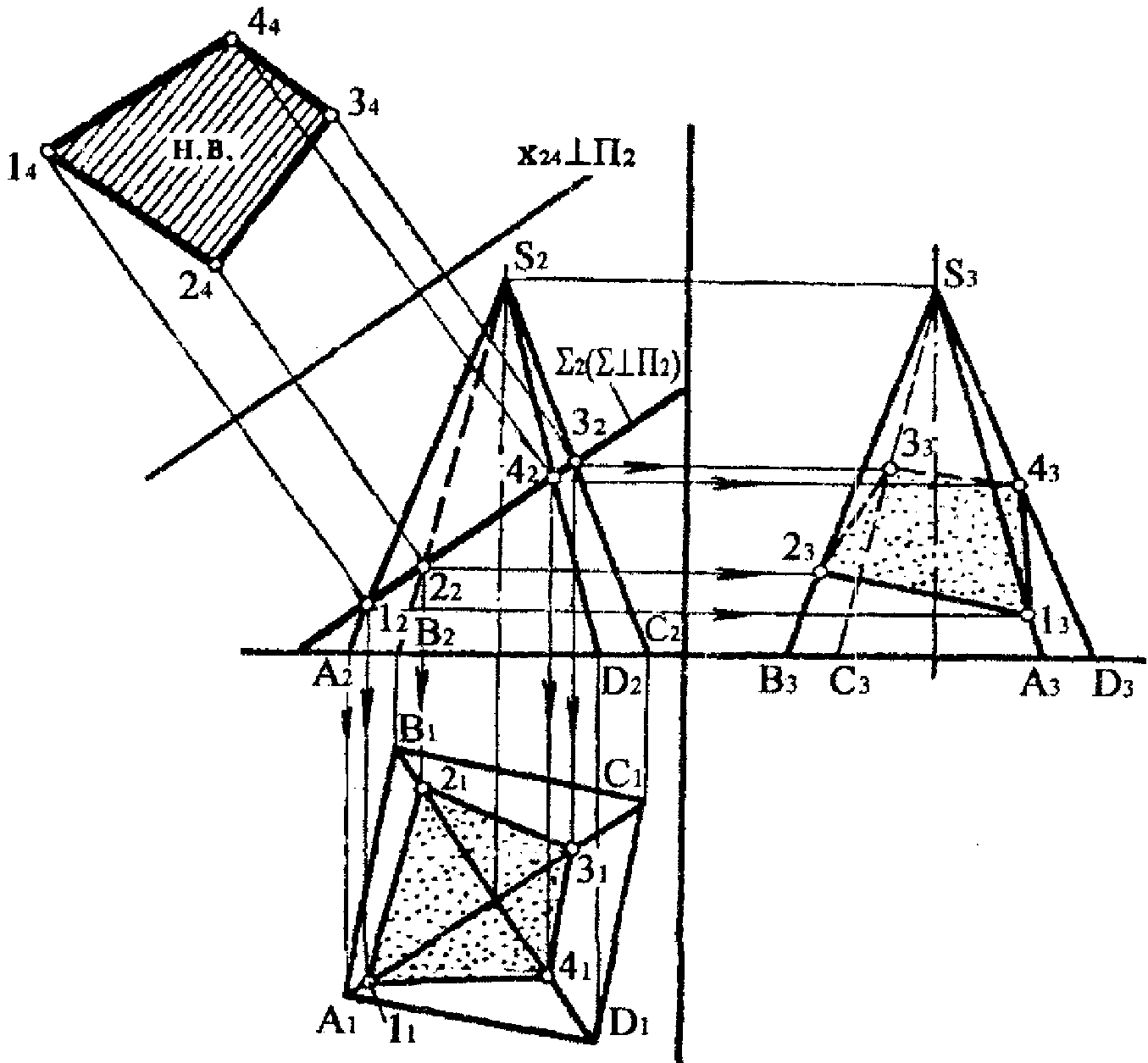
5.3 Дати відповіді на запитання стосовно кресленика, що наведене на рисунку 5.3.
1) Який багатогранник заданий на рисунку?
- На рисунку 5.3 заданий багатогранник, що називається _____________________
_____________________________________________________________________________
2) З яких багатокутників складаються грані багатогранника?
- Грані багатогранника складаються з _____________________________________ .
3) Які багатогранники називають тетраедрами?
- Тетраедром називають тригранну піраміду, у якій бокові грані і основа є ____________________________________________.
|
| Рисунок 5.3 |
4) Які положення у просторі займають ребра і грані багатогранника, що наведений на рисунку 5.3?
- Ребра і грані багатогранника займають ___________________ положення.
5) Яке положення у просторі займає січна площина S ?
- Січна площина S займає ________________________ положення.
6) По якій фігурі січна площина S перетинає багатогранник і чому?
- Січна площина S перетинає багатогранник по _____________, тому що вона перетинає ____ грані багатогранника.
7) Яким способом на рисунку 5.3 визначена фігура перерізу багатогранника січною площиною?
- Фігура перерізу багатогранника січною площиною визначена як результат перетину фронтальних проекцій ________________ багатогранника з ______________________ слідом-проекцією січної площини.
8) Яким способом визначена натуральна величина фігури перерізу багатогранника січною площиною?
- Натуральна величина фігури перерізу багатогранника січною площиною визначена способом ___________________________________.
5.4 Наведіть алгоритм побудови точок перетину прямої з чотирьохгранної призмою (рисунок 5.4 а, б) одночасно для двох рисунків а) і б).
|
| а) б) Рисунок 5.4 |
1) ___________________________________________________________
__________________________________________________________________
__________________________________________________________________
2) ___________________________________________________________
__________________________________________________________________
__________________________________________________________________
5.5 Навести алгоритм побудови проекцій лінії перетину двох призм, що наведені на рисунку 5.5.
1) ___________________________________________________________
__________________________________________________________________
__________________________________________________________________
2) ___________________________________________________________
____________________________________________________________________
| |
| Рисунок 5.5 |
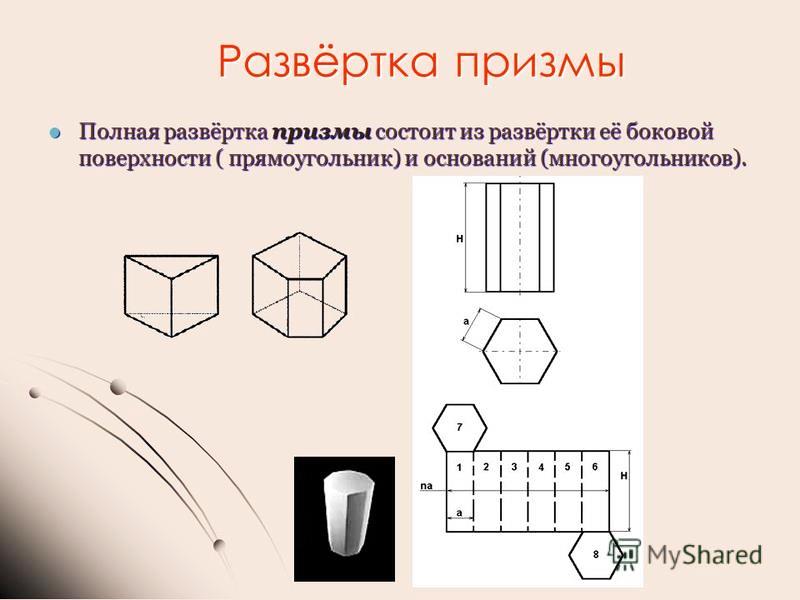
Рисунок 5.6 – Приклад розгортки прямої призми
ЗАПИТАННЯ ДЛЯ САМОПЕРЕВІРКИ
з теми “ Багатогранники. Взаємний перетин багатогранників ”
1 Що називають багатогранником?
2 Що створює сітку багатогранника?
3 Як утворюється ребро багатогранника?
4 Як будуються проекції багатогранника?
5 Які плоскі фігури можуть утворитися при перетині куба площиною?
6 Якими способами можна побудувати переріз багатогранника площиною?
7 Якими способами можна побудувати лінію перетину двох багатогранників?
ЛЗ-6 Дослідження властивостей поверхонь обертання
Мета вивчення теми і виконання графічної роботи:
- набуття вміння будувати кресленика технічних форм і розв’язувати за ними різні інженерно-технічних завдання.
знати:
- теоретичні основи побудови креслень;
уміти:
- виконувати кресленика простіших технічних форм;
- навчитися самостійно працювати над розв’язанням індивідуального завдання.
Література:
[1,с. 140 - 178], [2, с. 62 - 75], [3, с. 61-71]; [4, с. 49 – 53].
Навести відповіді та виконати графічні побудови в робочому зошиті на поставлені запитання
6.1 Яким чином утворюються поверхні обертання і який вигляд має їх визначник?
_____________________________________________________________
__________________________________________________________________
__________________________________________________________________
6.2 Які лінії утворюють ортогональну сітку поверхонь обертання? Наведіть їх назви і як вони утворюються?
_____________________________________________________________
__________________________________________________________________
__________________________________________________________________
6.3 Які лінії на поверхні обертання називають екватором, а які шийкою?
_____________________________________________________________
__________________________________________________________________
6.4 Яким чином на кресленні задають поверхню обертання?
_____________________________________________________________
__________________________________________________________________
6.5 Яким чином на кресленні за заданими віссю обертання і твірною будують головний меридіан поверхні?
1) ___________________________________________________________
2) ___________________________________________________________
__________________________________________________________________
__________________________________________________________________
6.6 Які поверхні обертання називають поверхнями другого порядку?
_____________________________________________________________
__________________________________________________________________
__________________________________________________________________
6.7 Запишіть теорему про перетин двох алгебраїчних поверхонь.
Теорема. _____________________________________________________
__________________________________________________________________
__________________________________________________________________
6.8 По яким лініям поверхня обертання другого порядку може пересікатися із січною площиною, назвіть їх.
- Поверхня обертання 2-го порядку із січною площиною може пересікатися по кривим _____________ порядку:
- по ____________________________,
- по ____________________________,
- по ____________________________ ,
або по __________ прямим:
6.9 Сфера із січною площиною перетинається по ______________ .
6.10 Поверхня циліндру обертання в залежності від розташування січної площини відносно неї може бути перерізаною по:
- ______________________________ ,
- ______________________________ , або
- __________________________________ .
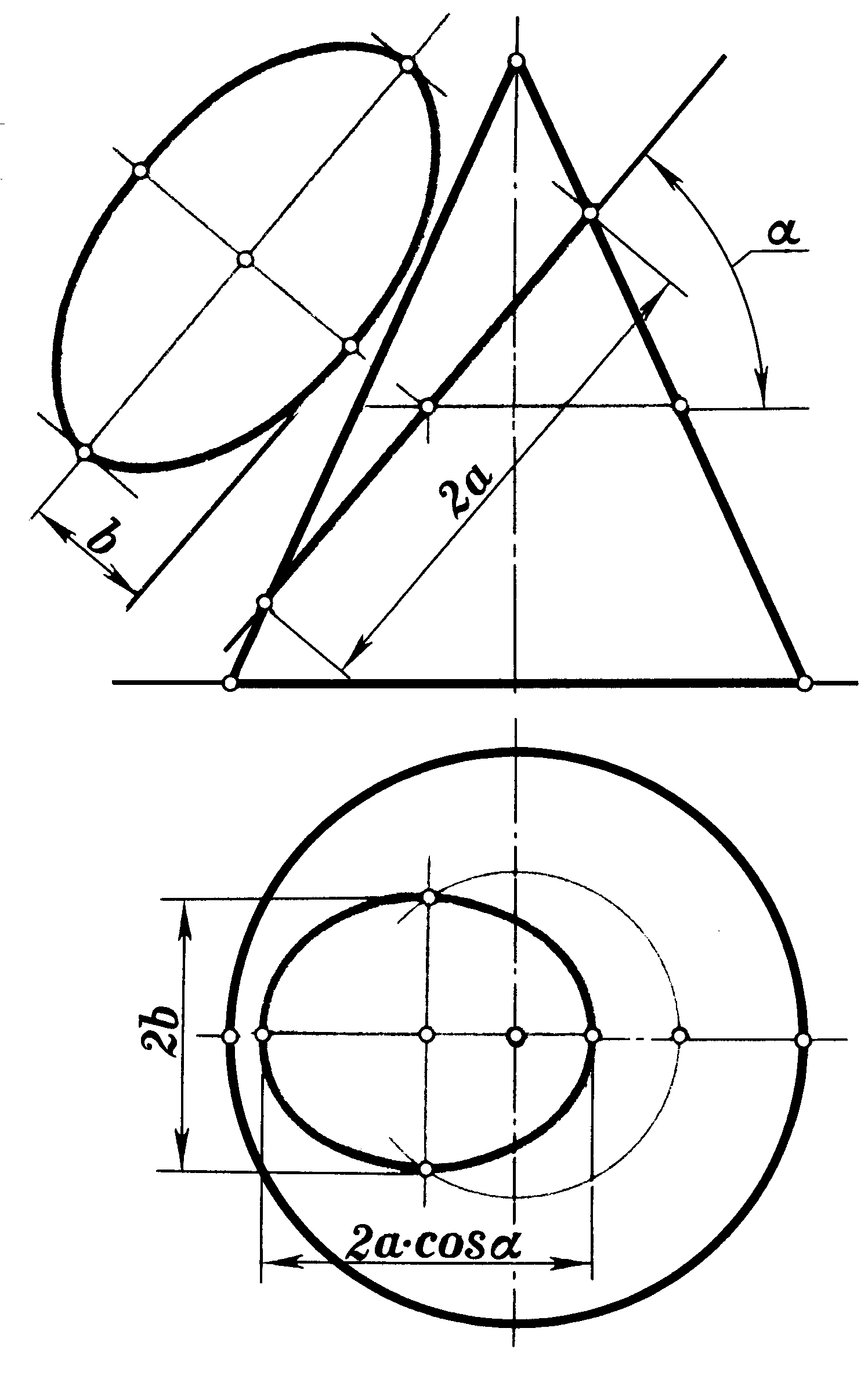
6.11 Назвіть назву лінії перерізу конічної поверхні січною площиною (рисунки 6.1; 6.2; 6.3). Відповіді наведіть у таблиці 6.1.
| 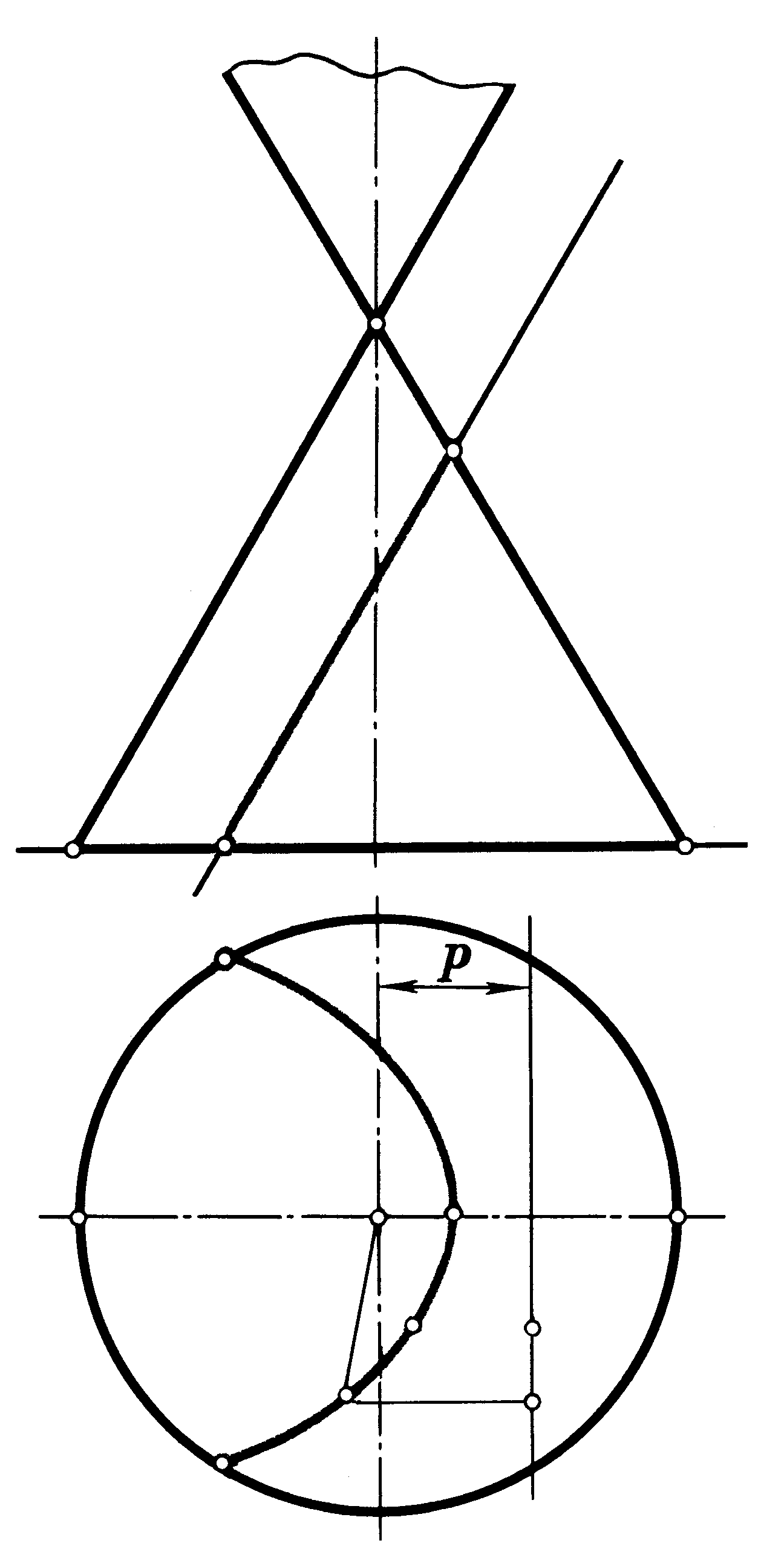
| 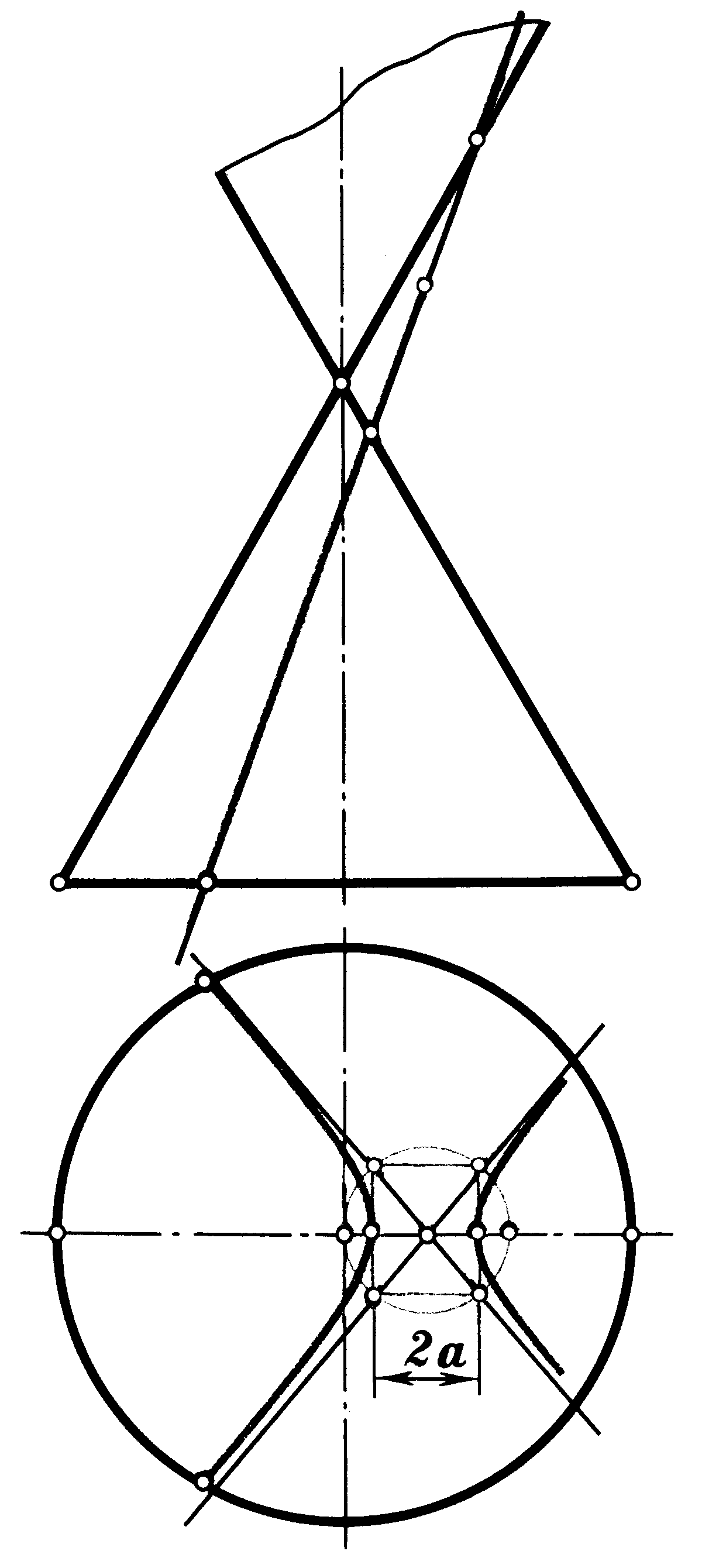
|
| Рисунок 6.1 | Рисунок 6.2 | Рисунок 6.3 |
Таблиця 6.1 – Відповіді на запитання 6.11
| Рисунок | Назва лінії перерізу конічної поверхні січною площиною і як вона розташована відносно конічної поверхні |
| 6.1 | |
| 6.2 | |
| 6.3 |
6.12 На рисунку 6.4 наведене кресленика конусу, поверхня якого перерізана призматичним вікном. Грані вікна перерізали конічну поверхню по відповідним лініям. Назвати ці лінії, відповіді записати у таблицю 6.2. Визначити, яким способом побудовані проекції ліній перетину конічної поверхні з гранями призматичного вікна.

|
| Рисунок 6.4 |
Таблиця 6.2 – Відповіді на запитання 6.12
| Назва грані призми | Назва лінії перерізу конічної поверхні гранями призматичного вікна і обґрунтуйте цей тип лінії |
| 1- 8 | |
| 3- 8 | |
| 1- 3 |
- Проекції ліній перетину поверхні конусу гранями призматичного вирізу побудовані за допомогою способу ___________________________
__________________________________________________________________.
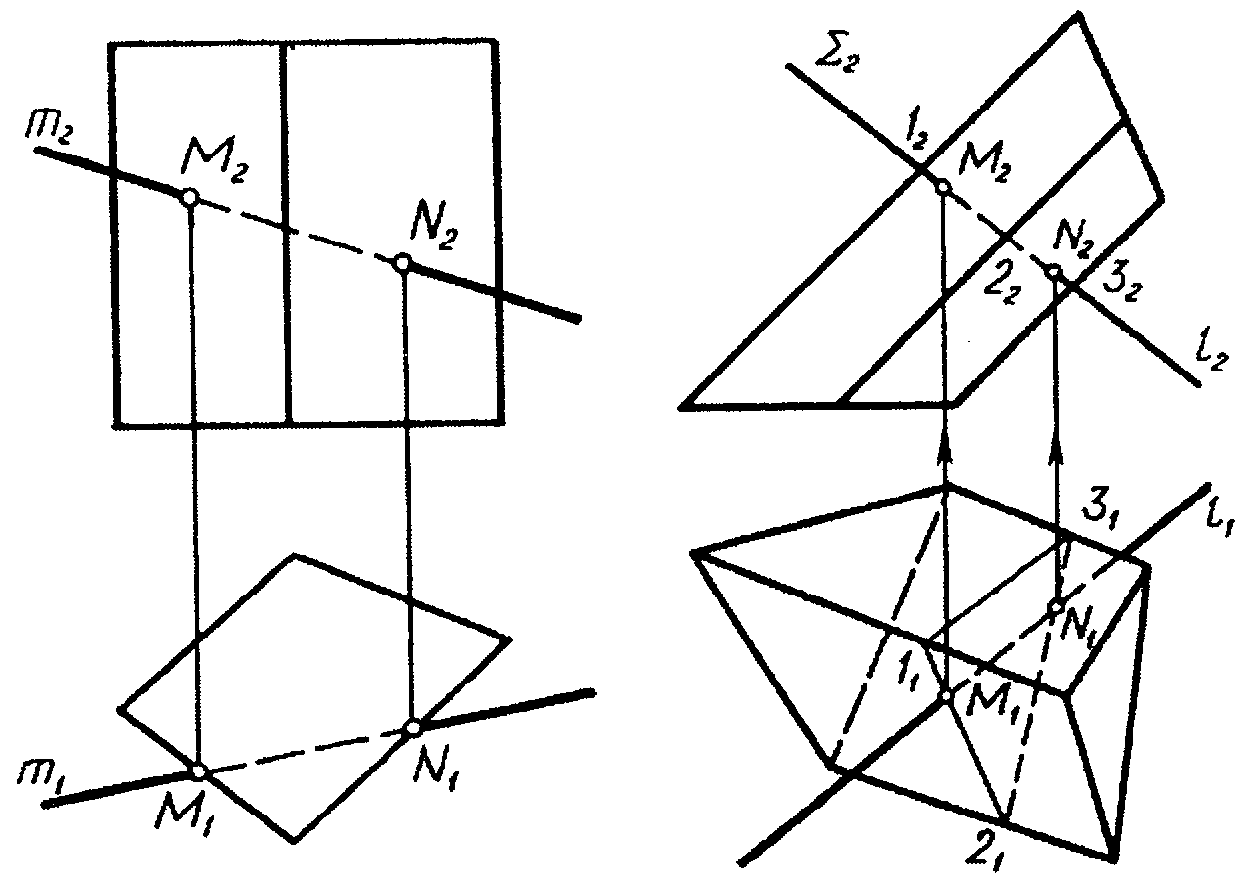
6.13 По якій лінії перерізана куля фронтально-проекційною площиною Ф (рисунок 6.5) і яким чином вона проектувалась на площини проекцій П1, П2, П3 ? Яким способом побудовані проекції точок перерізу кулі фронтально-проекційною площиною Ф ?
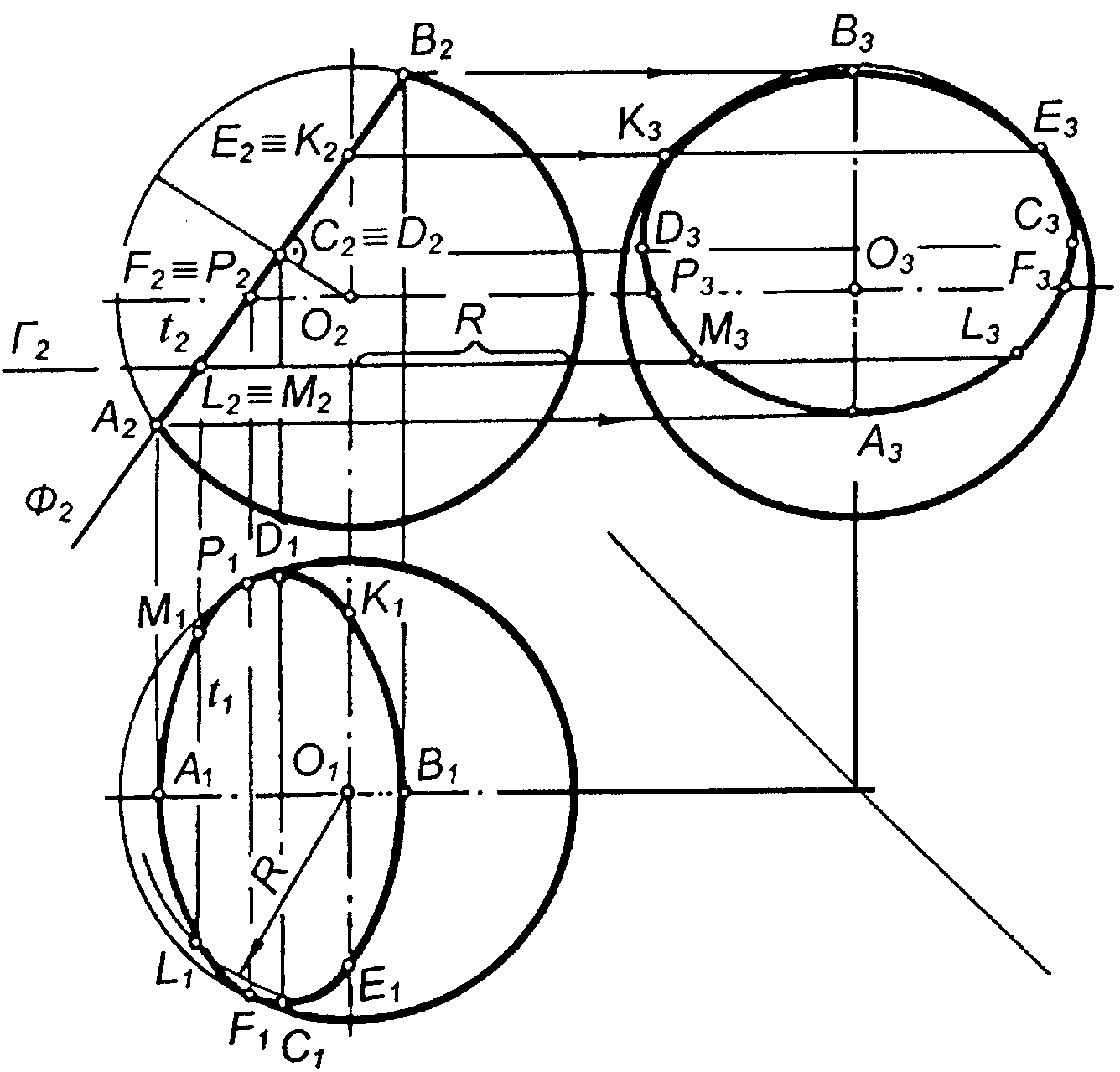
|
| Рисунок 6.5 |
Відповідь: куля перерізана фронтально-проекційною площиною Ф по __________________(вид перерізу), проекціями якого на площини проекцій П1 і П3 є ___________________, а на П2 - ________________________ .
Для побудови проекцій точок лінії перерізу кулі площиною застосований спосіб _____________________________________________ .
6.14 Запишіть теорему Монжа про розпадання кривої 4-го порядку при взаємному перетинанні двох поверхонь 2-го порядку на дві плоскі криві другого порядку (рисунок 6.6).________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
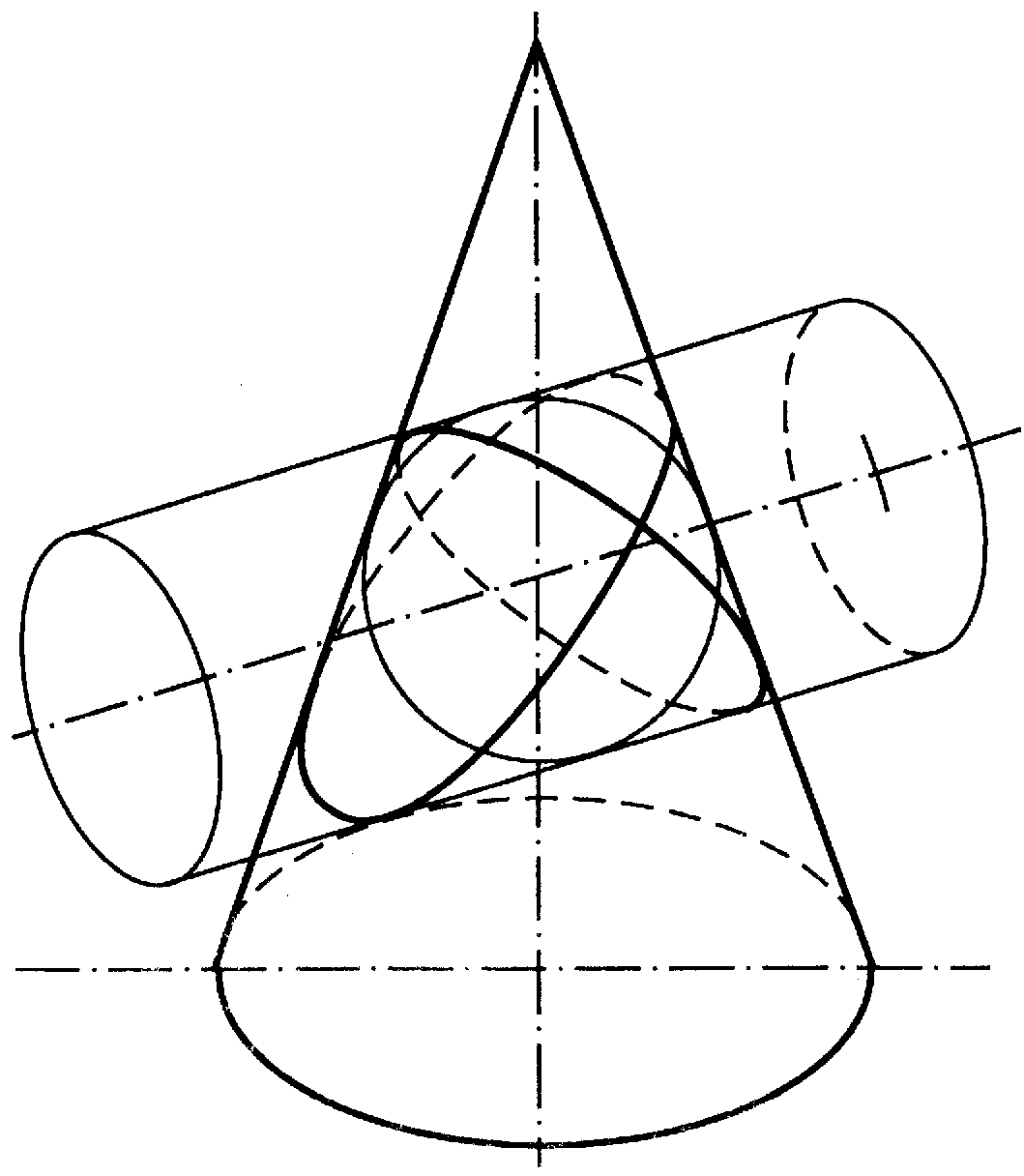
|
| Рисунок 6.6 |
Теорема Монжа. _____________________________________________
__________________________________________________________________
__________________________________________________________________
__________________________________________________________________
6.15 Визначити, за якими лініями перетинаються дві поверхні, що задані на рисунках 6.7; 6.8; 6.9. Відповідь наведіть у таблиці 6.3.

| 
| 
|
| Рисунок 6.7 | Рисунок 6.8 | Рисунок 6.9 |
Таблиця 6.3 – Відповіді на запитання 6.15
| Рисунок | Назва ліній перетину заданих поверхонь і чому саме такі лінії |
| 6.7 | |
| 6.8 | |
| 6.9 |
Відповідь. _____________________________________________________________
________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
6.17 Назвіть вид проекцій на П1 і П2 просторової лінії 4-го порядку як перетину двох заданих поверхонь обертання другого порядку (рисунки 6.10; 6.11).
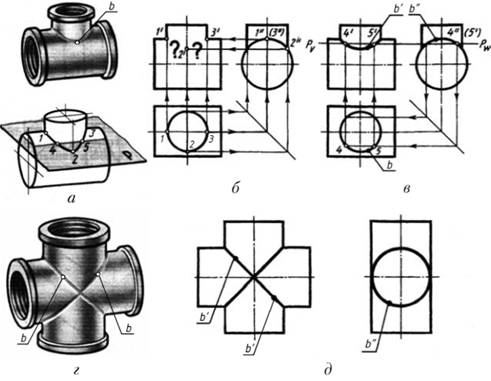
Рисунок 6.10
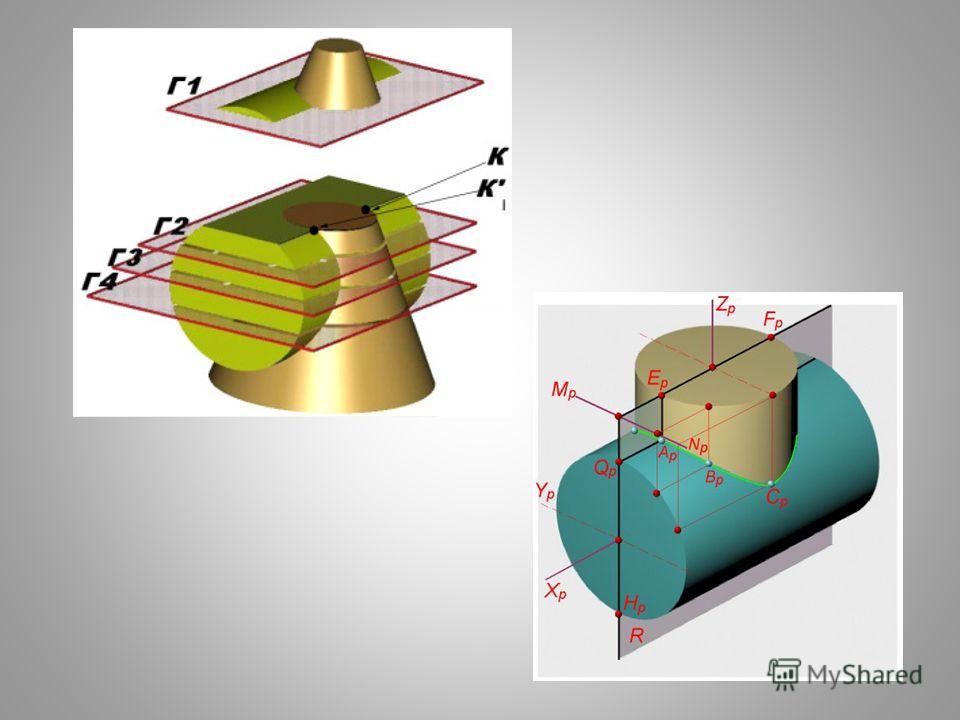
Рисунок 6.11
6.18 Наведіть алгоритм розв’язування задач на побудову лінії перетину двох поверхонь
1)__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
2) ___________________________________________________________
3) ___________________________________________________________
4) ___________________________________________________________
__________________________________________________________________
5) ___________________________________________________________
__________________________________________________________________
ЗАПИТАННЯ ДЛЯ САМОПЕРЕВІРКИ
з теми “ Поверхні обертання. Взаємний перетин поверхонь обертання ”
1 Визначення поверхні.
2 Основні способи завдання поверхонь.
3 Що називається визначником поверхні і із яких основних частин він складається?
4 Що називається безперервним каркасом ліній поверхні?
5 Що є основою кресленика поверхні?
6 Що таке обрис поверхні?
7 За якими критеріями класифікують поверхні?
8 Як утворюються поверхні обертання?
9 Назвіть характерні лінії поверхні обертання.
10 Як побудувати обрис поверхні обертання на кресленні, якщо твірна – просторова крива.
11 Які поверхні обертання називають поверхнями другого порядку?
12 Алгоритм визначення точок лінії перетину поверхні з площиною.
13 Які точки лінії перетину площини з кривою поверхнею називають головними або опорними?
14 Коли у перерізі конічної поверхні 2-го порядку отримують коло? Еліпс? Параболу? Гіперболу? Дві прямі?
15 Назвіть алгоритм графічних побудов при визначенні точок перетину поверхні прямою лінією.
16 Яку площину-посередник треба застосувати для побудови точок перетину прямої загального положення з поверхнею прямого кругового конуса?
17 Алгоритм побудови точок лінії перетин двох кривих поверхонь обертанні 2-го порядку.
18 Які поверхні-посередники зручно використовувати при побудові точок лінії перетину двох поверхонь обертання 2-го порядку?
19 Назвіть сутність способу застосовування січних площин-посередників при побудові точок лінії перетину двох поверхонь обертання 2-го порядку.
20 Які поверхні обертання називають співвісними?
21 По яким лініям перетинаються співвісні поверхні обертання?
22 Коли можна використати січні сфери при побудові точок лінії перетину двох кривих поверхонь?
23 По яким лініям перетинаються два прямих кругових циліндра однакового діаметру, якщо їх осі перетинаються? Чому?
24 Як визначається порядок лінії перетину двох алгебраїчних поверхонь?
25 Чому дорівнює порядок проекції лінії перетину двох алгебраїчних поверхонь при проекціюванні її на спільну площину симетрії двох поверхонь?
Дата: 2018-12-21, просмотров: 829.