1) Вивчити положення основного методу нарисної геометрії – методу проекціювання і надати курсантові методичну допомогу з цього напрямку.
2) Засвоїти терміни і поняття, що відносяться до методу проекціювання, розвинути технічне мислення і просторове уявлення.
В результаті вивчення теми і виконання графічних завдань курсант (студент) повинен
знати:
- теоретичні основи побудови комплексних креслень (епюрів) основних геометричних фігур: точок, прямих, площин;
уміти:
- будувати ортогональні проекції точок, прямих, площин;
- читати комплексні кресленика основних геометричних фігур, тобто визначати їх положення у просторі відносно координатних площин проекцій;
- за комплексним кресленикам відрізку прямої знаходити її дійсну величину та кути нахилу до координатних площин проекцій;
- навчитися самостійно працювати над розв’язанням індивідуального завдання.
Література:
[ 3, с. 20-24] ; [ 4, с. 11-18] ; [ 5, розділи с.11-19] .
Самостійна теоретична підготовка до заняття:
Навести відповіді на поставлені запитання та виконати необхідні графічні побудови в робочому зошиті
2 .2.1 Для побудови комплексного кресленика застосовують основний метод нарисної геометрії – метод ___________________________________
на ___________________________________ площини проекцій.
(яким чином розташовані?)
2.2.2 Лінія перетину двох координатних площин проекцій називається _____________________________________________________________________________.
2.2.3 Лінія, що зв’язує між собою дві проекції точки, називається лінією ___________________________________________________________.
2.2.4 Якщо на будь-якій прямій або осі проекцій встановити систему координат, то вона перетворюється у ________________________________________________________.
2.2.5 До системи координат відносять: 1) _________________________. 2) _____________________________________, 3) _______________________ .
2.2.6 Координата – це _____________, що визначає положення точки у заданій системі координат.
2.2.7 Положення точки у тривимірному просторі (R3) визначається (скількома?) ____________ координатами (назвіть їх) __________________.
2.2.8 Під вимірністю простору розуміють ___________________________________
_________________________________________________________________.
2.2.9 Координатні площини проекцій позначають великою літерою грецького алфавіту П (пі) з нижніми індексами 1, 2 або 3.
Площина П1 – це _________________________ площина проекцій;
площина П2 – це _________________________ площина проекцій;
площина П3 – це _________________________ площина проекцій.
На рисунку 2.1 позначте три координатні площини проекцій П1, П2, П3 і відповідні їм осі проекцій, як результат перетину двох площин проекцій.
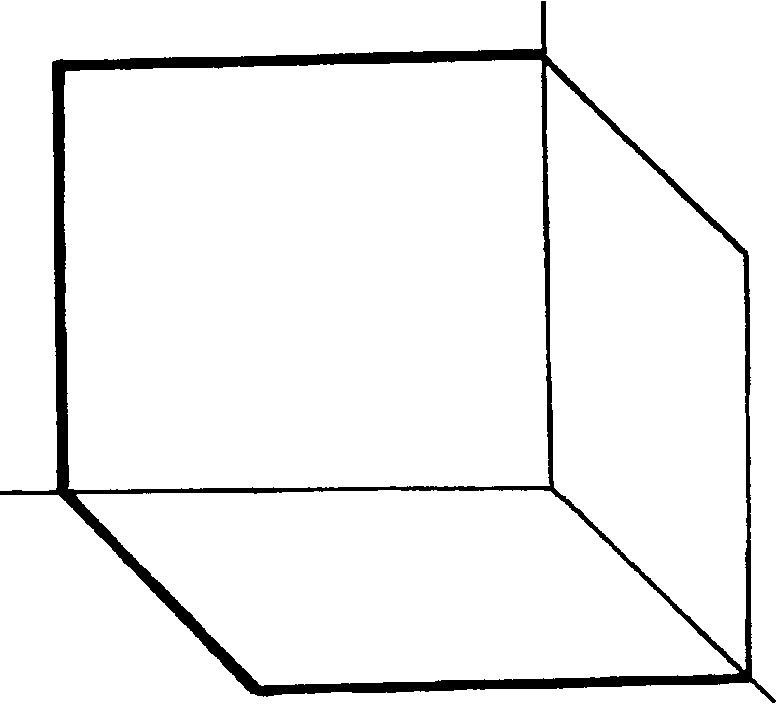
Рисунок 2.1 – Координатні площини та осі проекцій
2.2.11 Вісь проекцій відрізняється від осі координат тим, що _________
__________________________________________________________________.
2.2.12 Моделлю тривимірного простору є ________________________
__________________________________________________________________.
2.2.13 Проекційною моделлю тривимірного простору є _____________
__________________________________________________________________.
2.2.14 Запис типу А (30, 20, 35) означає, що 30 – це координата _____, яка визначає відстань точки А від координатної площини ______; 20 – це координата ____, яка визначає відстань точки А від координатної площини ______, 35 – це координата ____, яка визначає відстань точки А від координатної площини ______.
На моделі тривимірного простору (R3) – декартовій системі осей координат Oxyz (рисунок 2.2) :
– побудувати точку А за допомогою заданих її трьох координат x , y , z;
– навести координатну ламану Oxyz точки А суцільною товстою основною лінією;
– побудувати три проекції А1, А2, А3 точки А.
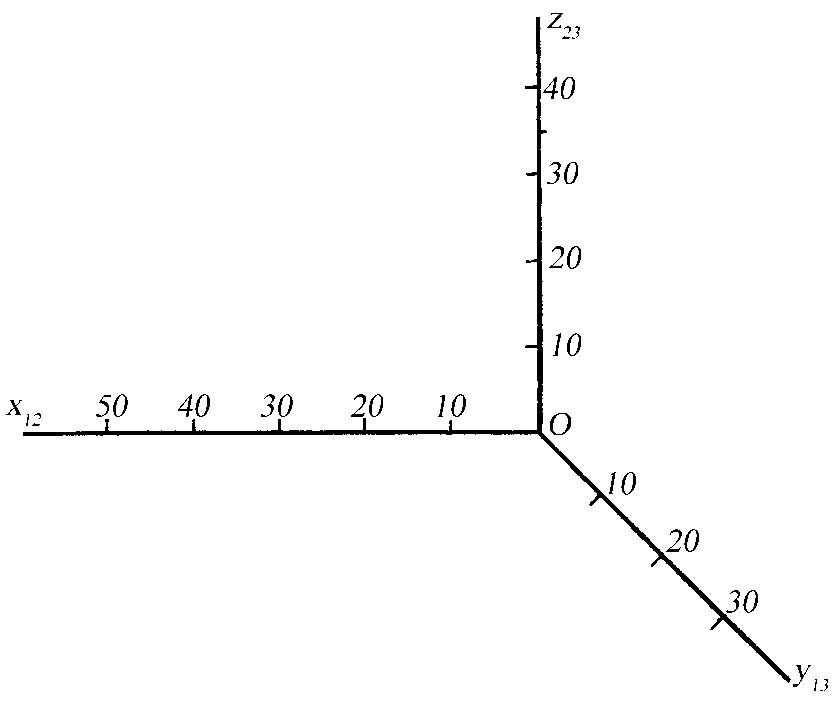
Рисунок 2.2 – Модель тривимірного простору
2.2.15 Задані три точки: А (20, 10, 45);
В (50, 20, 25);
С (35, 35, 0).
Точка ____ має найбільше віддалення від площини проекцій _______, бо вона має найбільшу координату x = 50 мм, точка ______ розташована у площині проекцій ________, бо її координата z = 0 мм, точка ______ однаково віддалена від площин проекцій ______ і ______ , бо її координати x = y = 35 мм.
Якщо точка однакова віддалена від будь-яких двох координатних площин проекцій, то вона розташована у бісекторній площині, що поділяє двогранний прямий кут між цими площинами навпіл.
2 .2.16 Що називається визначником геометричної фігури?
Визначником геометричної фігури називається ____________________
__________________________________________________________________
______________________. Наприклад, визначником точки є ______________
__________________________________________________________________.
2.2.17 Яким чином отримують епюр (або комплексне кресленика) геометричної фігури, наприклад, точки ?
______________________________________________________________________________________________________________________________________________________________________________________________________
На рисунку 2.3 побудуйте епюр точки А, просторове зображення якої наведено на рисунку 2.2.
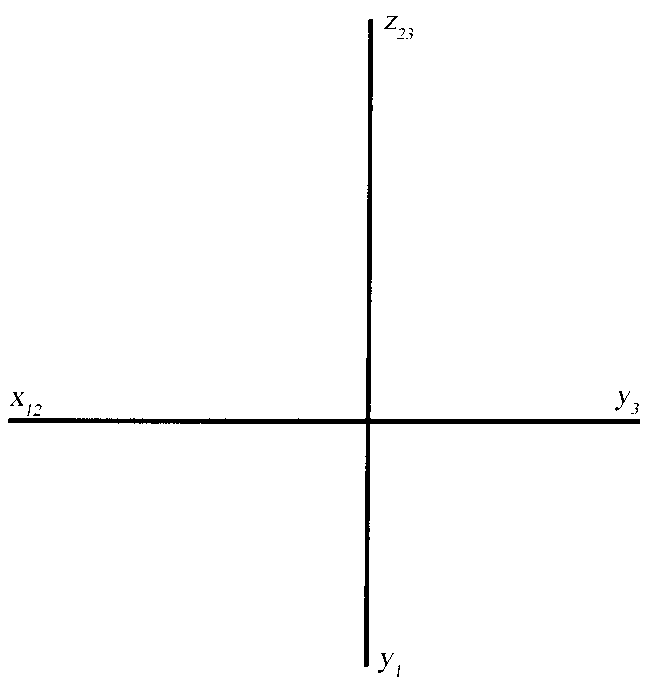
Рисунок 2.3 – Епюр точки А , або комплексне кресленика її
2.2.18 На епюрі положення фігури у тривимірному просторі визначають будь-які її _______ проекції (і чому?), бо вони утримують у собі всі (скільки?) ___________________ координати.
2.2.19 Основні позиційні властивості проекцій точки на епюрі зводяться до наступних:
- горизонтальна А1 і фронтальна А2 проекції точки А завжди розташовуються на одній __________________( якій?) лінії проекційного зв’язку;
- фронтальна А2 і профільна А3 проекції точки А завжди розташовуються на одній __________________( якій?) лінії проекційного зв’язку.
2.2.20 .Наведіть алгоритм побудови епюру точки за її координатами.
1) _____________________________________________________________________
_____________________________________________________________________________
2) _____________________________________________________________________
____________________________________________________________________________________________________________________________________
3) _____________________________________________________________________
__________________________________________________________________
2.2.21 Горизонтальна проекція А1 точки А визначається координатами ____ і _____;
фронтальна проекція А2 точки А визначається координатами ____ і
_____;
профільна проекція А3 точки А визначається координатами _____ і_____.
2.2.22 Лабораторне заняття 2:
Виконання практичних вправ за методом ортогонального проекціювання.
2.2.23 За наведеними нижче рисунками 2.4 - 2.10 аксонометричних зображень різних положень у просторі відрізків прямих поруч накреслити їх епюри в системі трьох площин проекцій і написати назву положення у просторі R3 цих прямих.
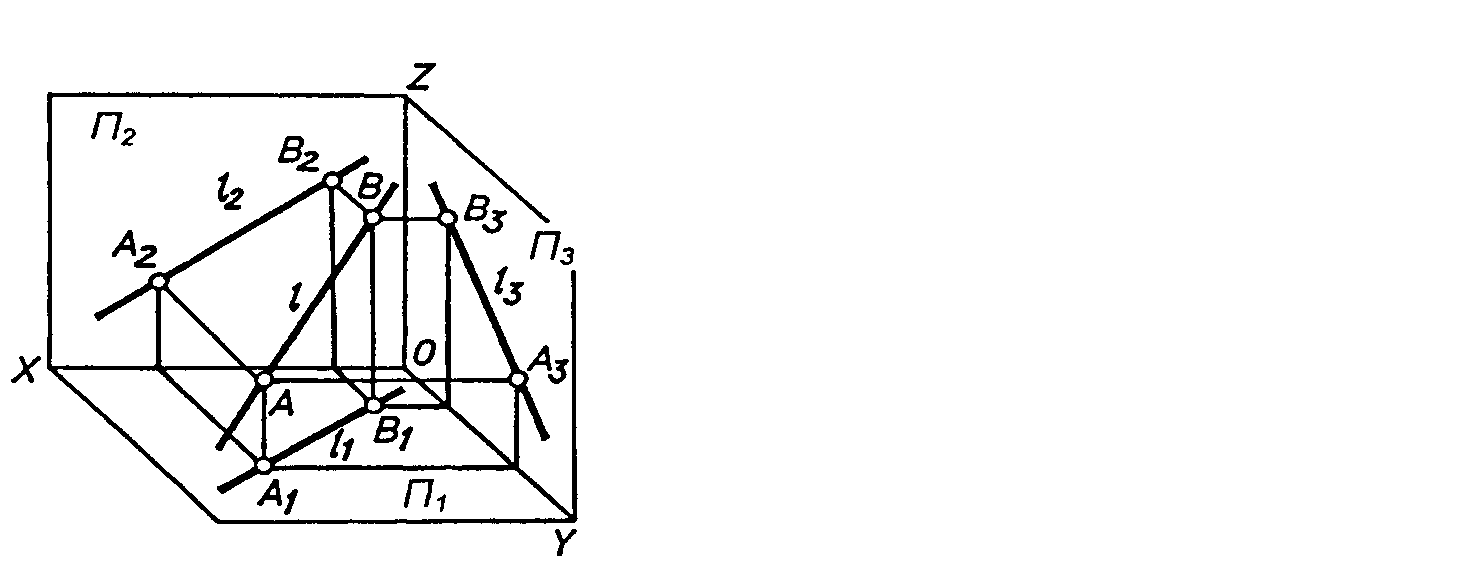
Рисунок 2.4 – Аксонометричне зображення
і епюр прямої ________________положення
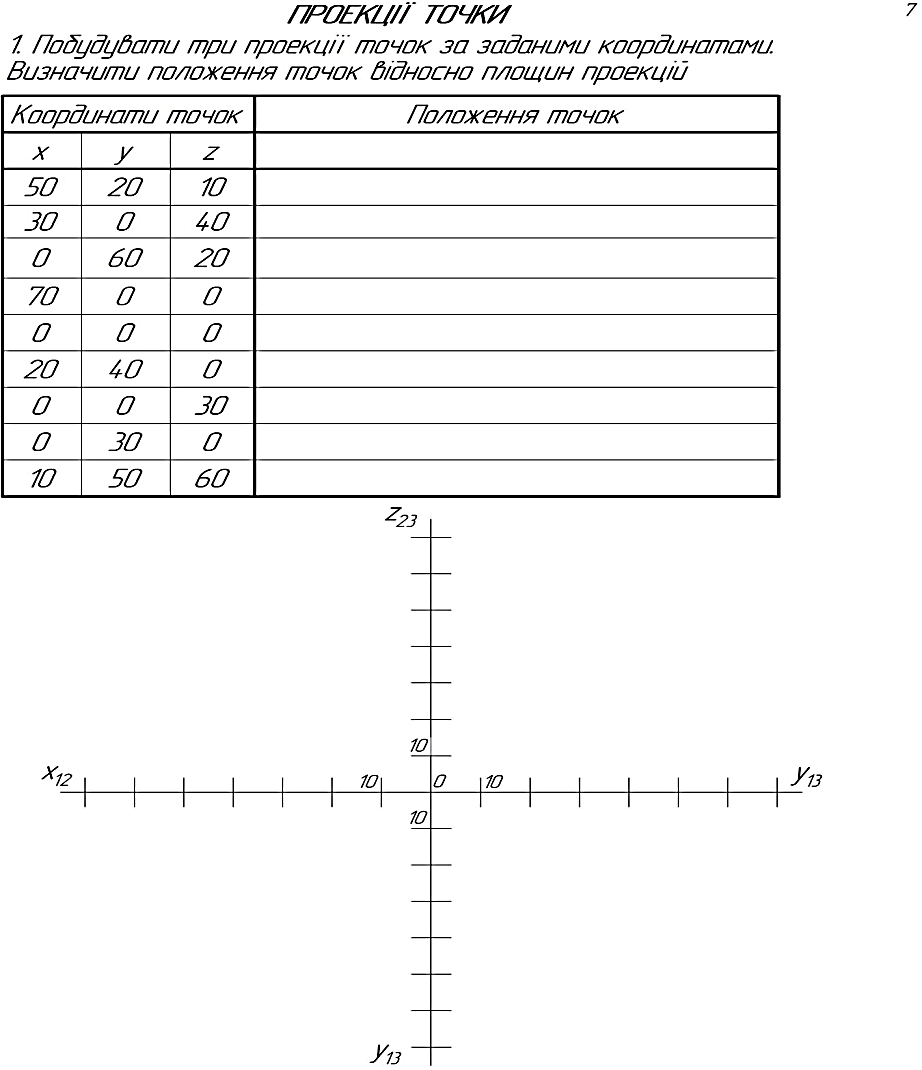
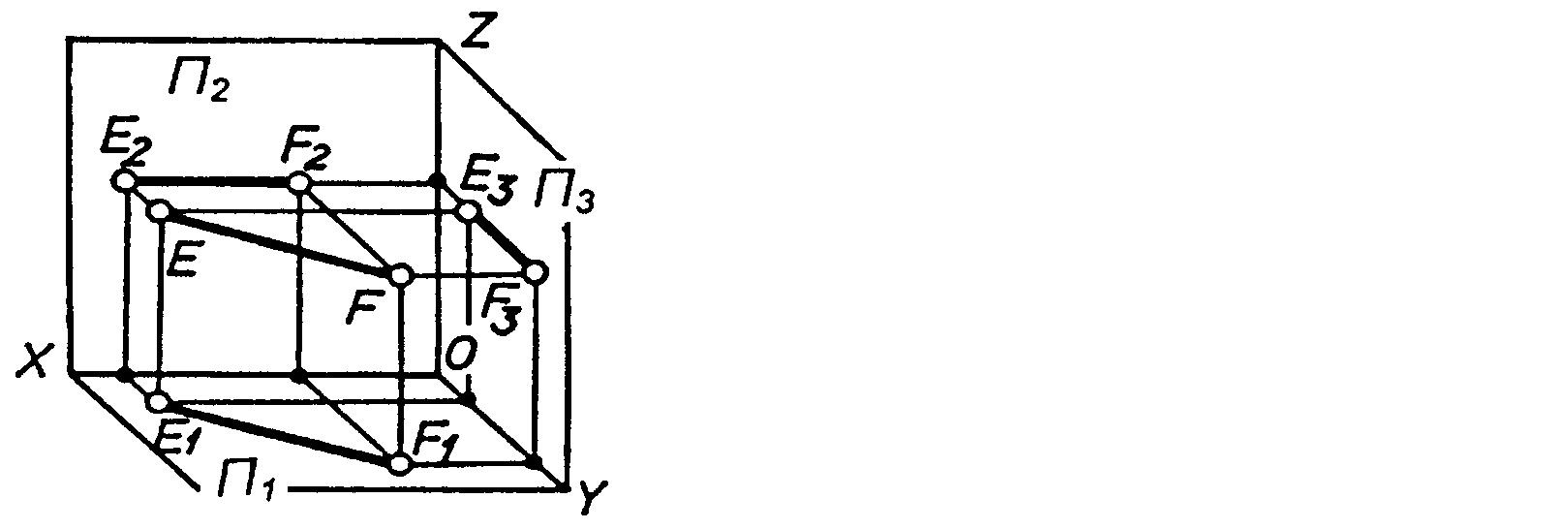
Рисунок 2.5 – Аксонометричне зображення і епюр прямої ________________
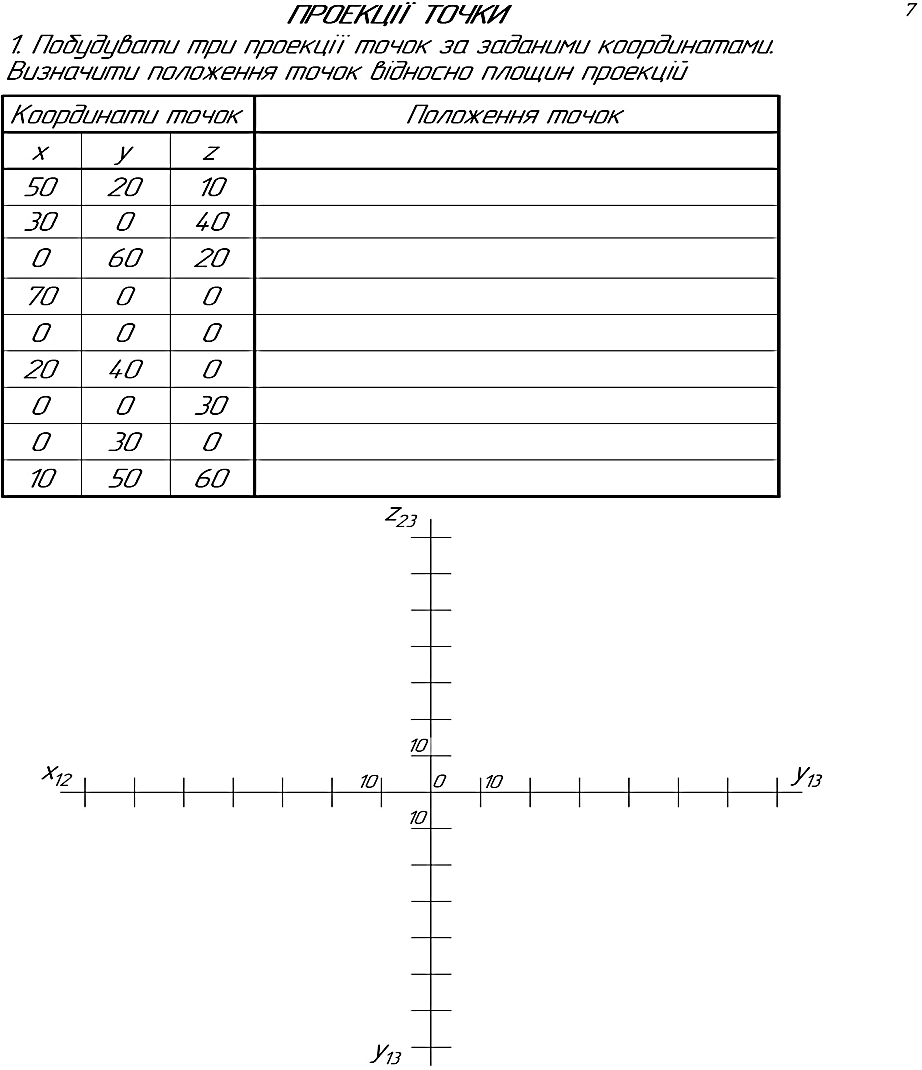
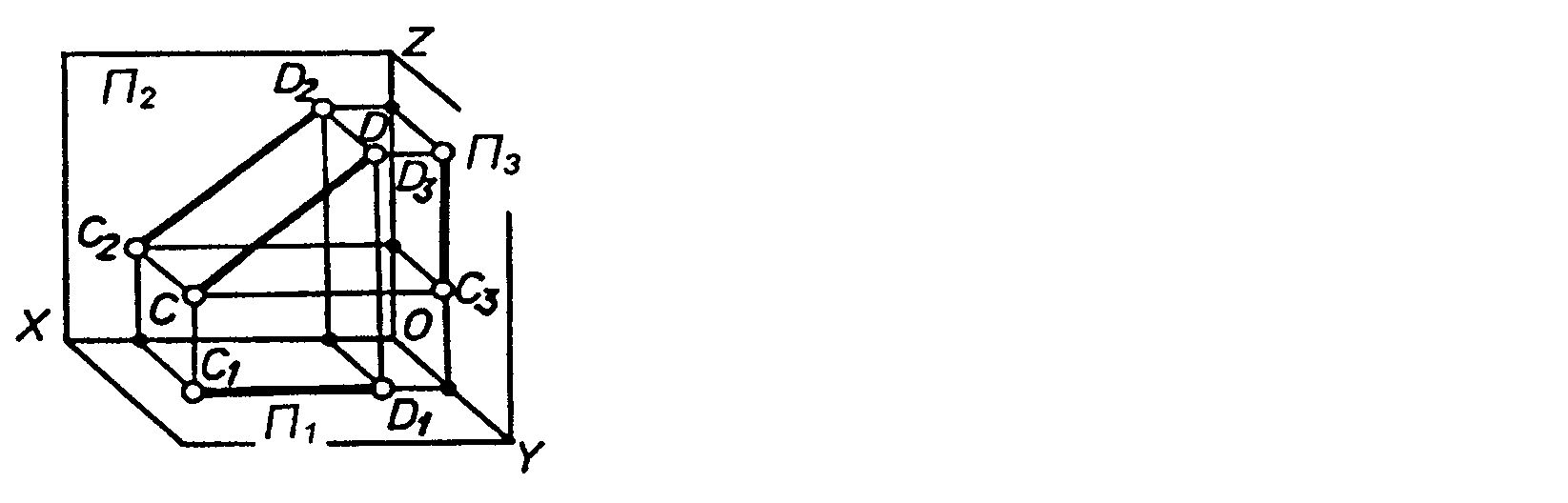
Рисунок 2.6 – Аксонометричне зображення і епюр прямої ________________
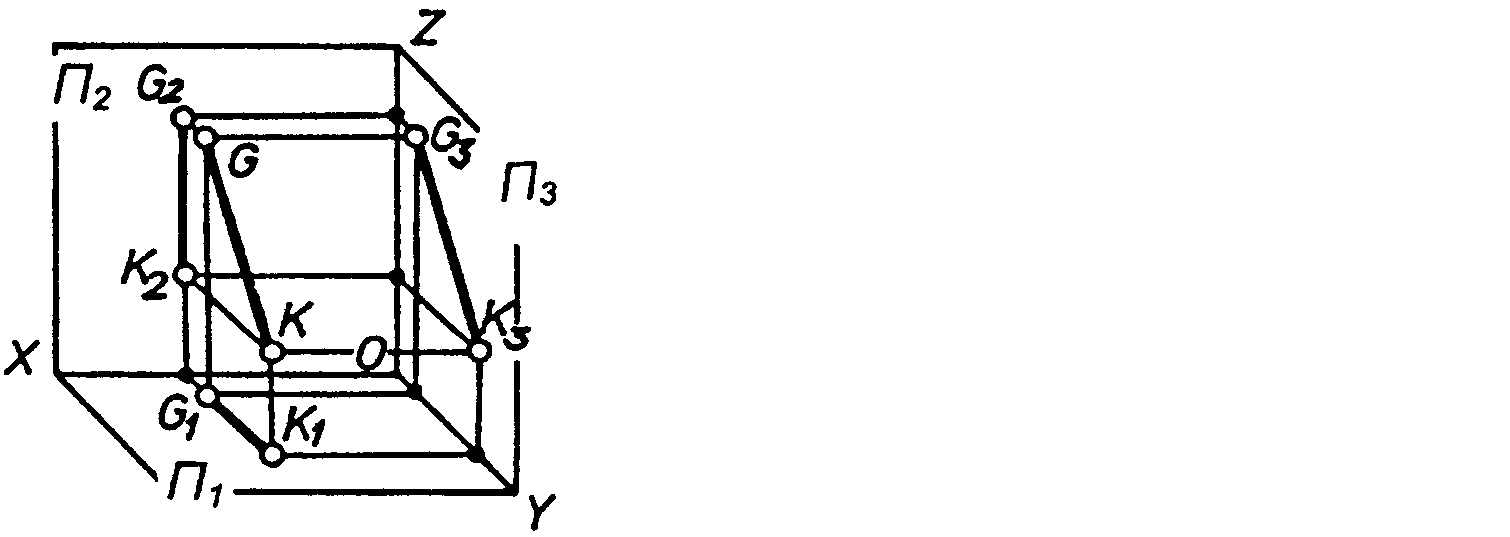
Рисунок 2.7 – Аксонометричне зображення і епюр прямої ________________
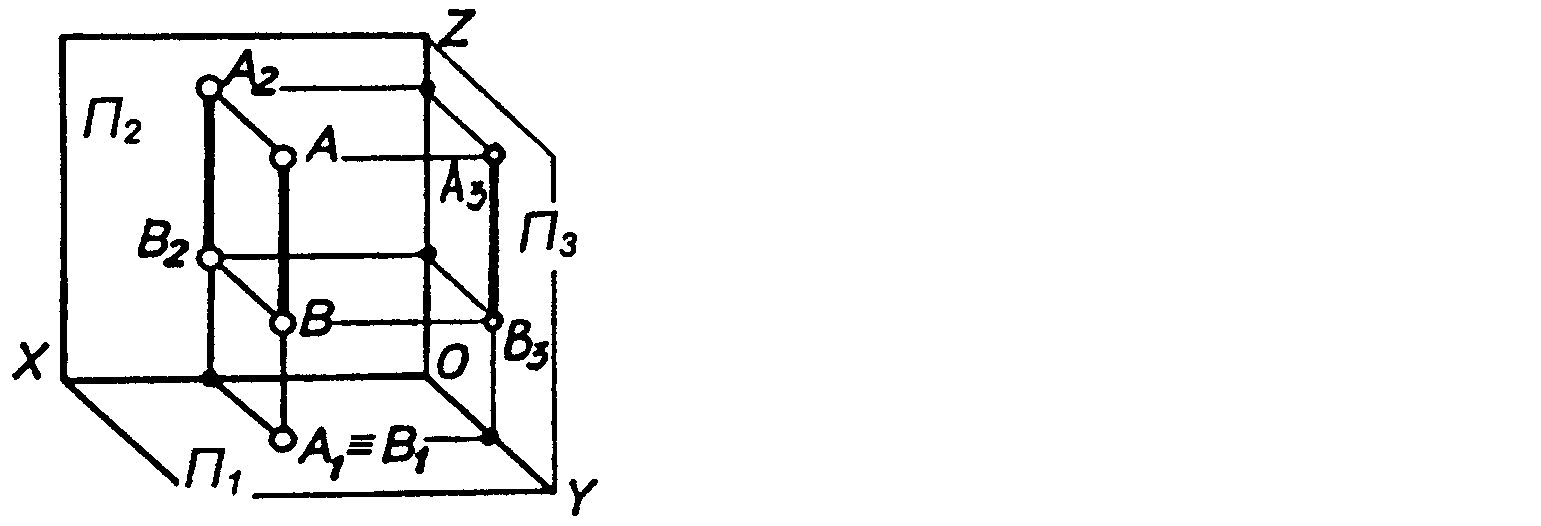
Рисунок 2.8 – Аксонометричне зображення і епюр прямої ________________
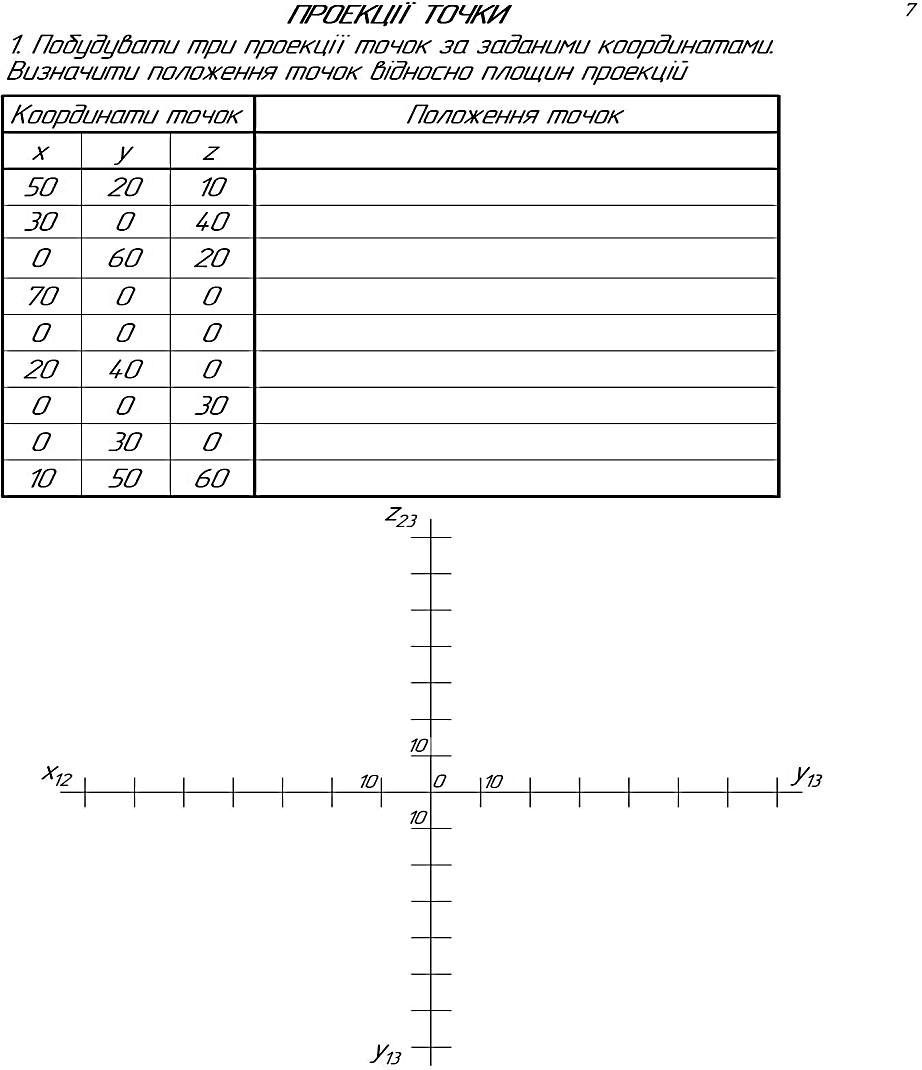
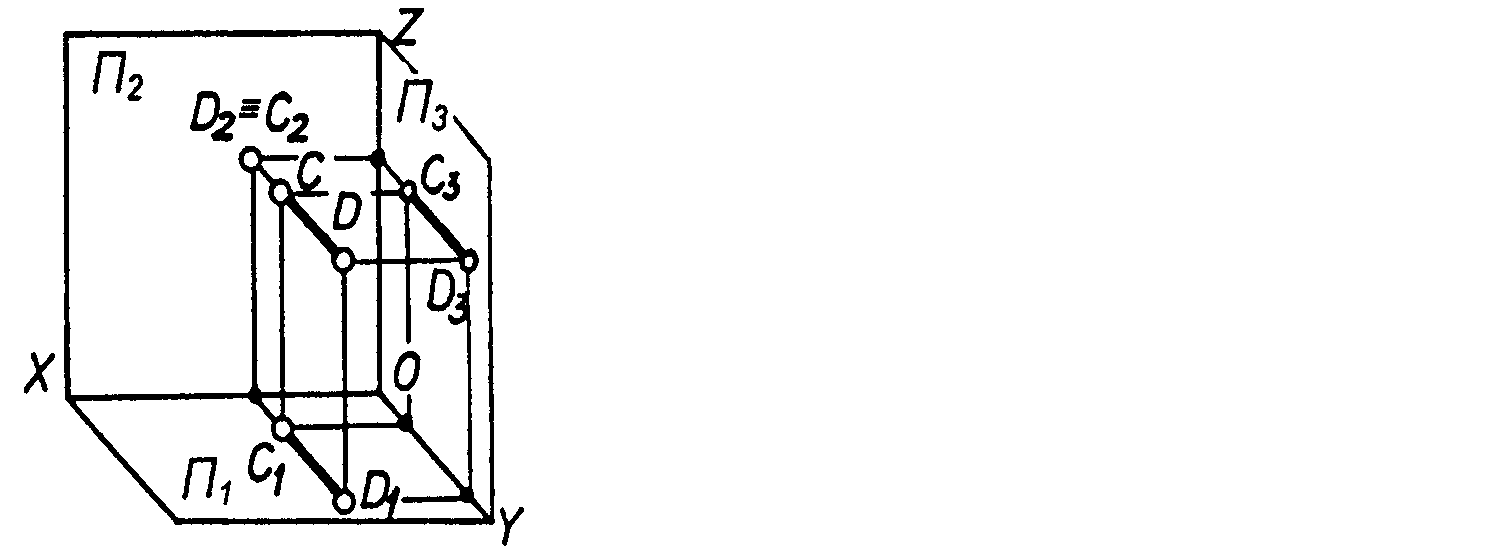
Рисунок 2.9 – Аксонометричне зображення і епюр прямої ________________
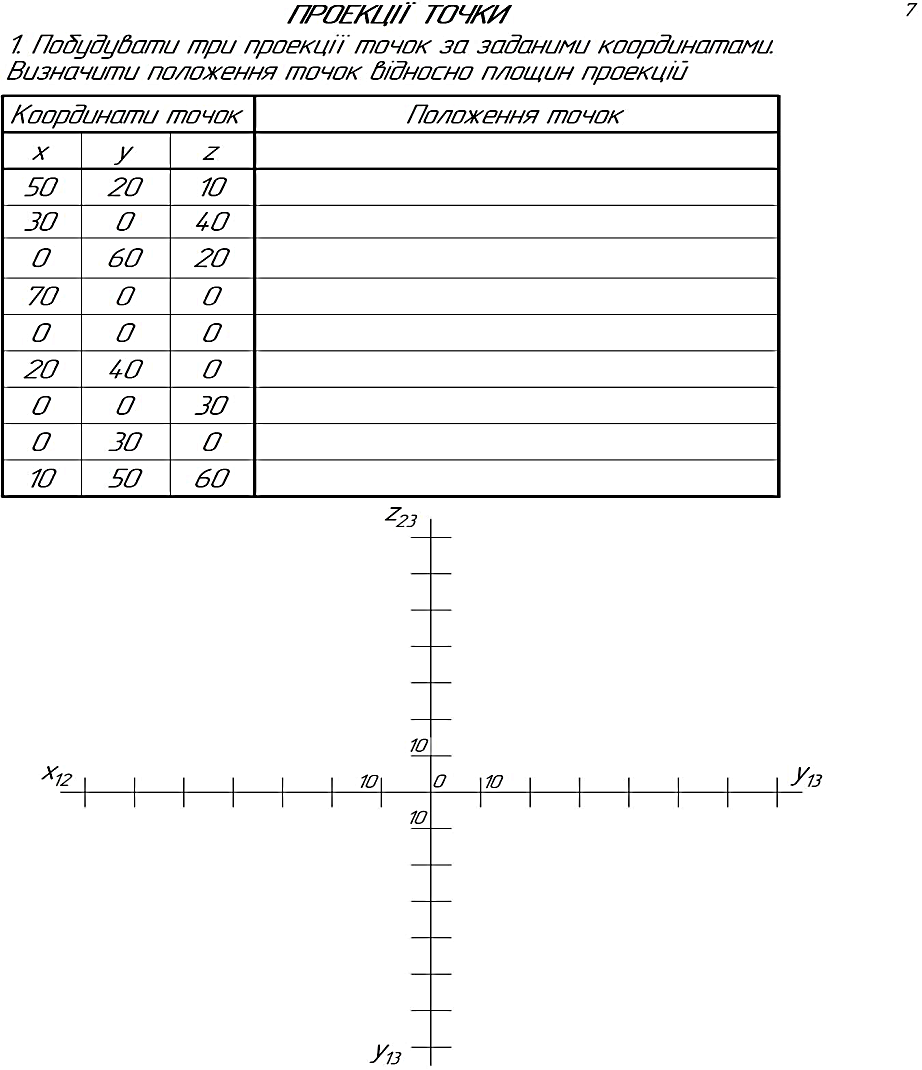
Рисунок 2.10 – Аксонометричне зображення і епюр прямої ________________
2.2.24 Щоб визначити величини прямих загального положення, необхідно скористатися способом прямокутного трикутника, суть якого полягає в наступному:
Правило прямокутного трикутника:
Щоб на епюрі визначити довжину відрізка загального положення, необхідно:
Дата: 2018-12-21, просмотров: 721.
