1) Вивчення позиційних властивостей проекцій шести пар геометричних фігур, що можна створити з основних трьох: Точки – Прямої - Площини .
2) Уміння за епюром будь-якої парі геометричних фігур визначити їх взаємне розташування у просторі.
В результаті вивчення теми і виконання графічних завдань курсант (студент) повинен
знати:
- теоретичні основи побудови креслень (епюрів) пар проекцій основних геометричних фігур: точок, прямих, площин, що певним чином розташовані між собою;
уміти:
- визначати за креслениками взаємні положення основних геометричних фігур між собою;
- будувати кресленика пар геометричних фігур за наперед заданими умовами їх взаємного розташування;
- навчитися самостійно працювати над розв’язанням індивідуального завдання.
Література:
[1,113 – 126], [2, с. 20 – 28], [3, с. 34-43]; [4, с. 19-34].
Самостійна підготовка до заняття курсанта(студента):
Навести відповіді на поставлені запитання та виконати графічні побудови в робочому зошиті
3.1 Дві точки у просторі можуть збігатися або не збігатися між собою. Якщо дві точки у просторі збігаються між собою, то насправді це буде одна точка, а не дві. На кресленику для однозначного визначення точки необхідно мати будь-які дві її проекції, бо вони мають всі три координати її, а відтак – її положення у просторі.
Інша справа, коли на кресленні якісь проекції двох точок збігаються між собою, але це ще не означає, що ми маємо справу з однією точкою.
3.1.1 Як розташовані у просторі дві точки, якщо одна пара однойменних проекцій їх збігається?
Якщо одна пара однойменних проекцій точок збігається між собою, то вони знаходяться на ____________________________________ .
3.1.2 Які точки називають конкуруючими?
Конкуруючими називають точки, що знаходяться на ________
__________________________________________________________________________ .
3.2 Визначити взаємне розташування точок, що показані на рисунку 3.1 а, b, c. Відповідь наведіть у таблиці 3.1.
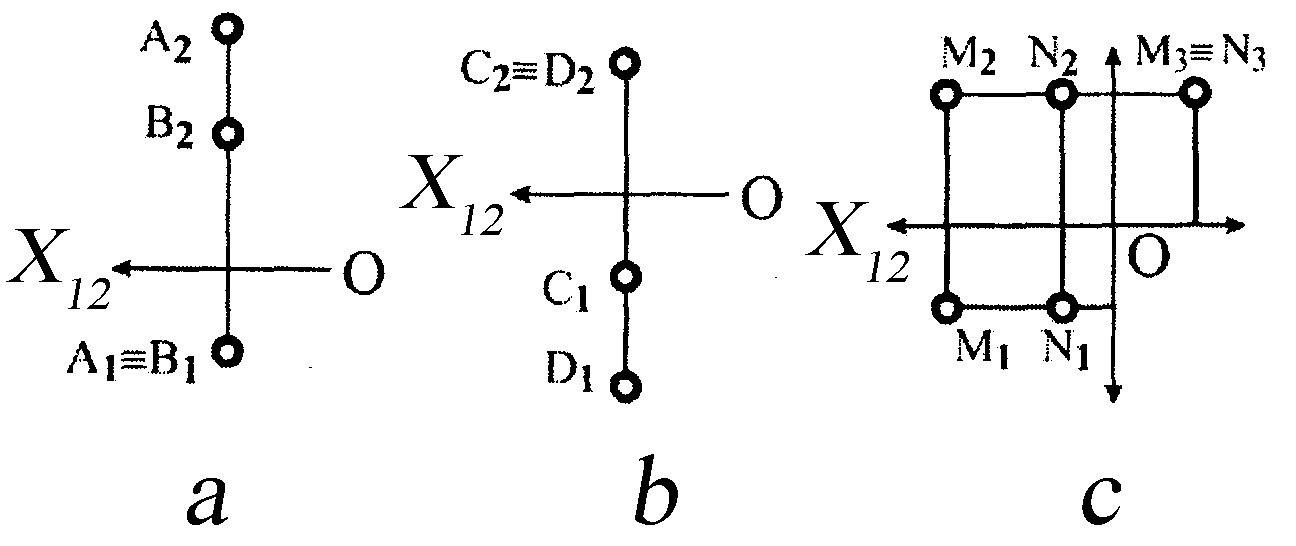
|
| Рисунок 3.1 |
Таблиця 3.1 – Відповіді на запитання 3.2
| Точки | Відповідь - точки розташовані: |
| А, В | на |
| C,D | на |
| M,N | на |
3.3 Визначити взаємне розташування точки відносно заданої прямої (рисунки 3.2; 3.3; 3.4; 3.5). Відповідь наведіть у таблиці 3.2.
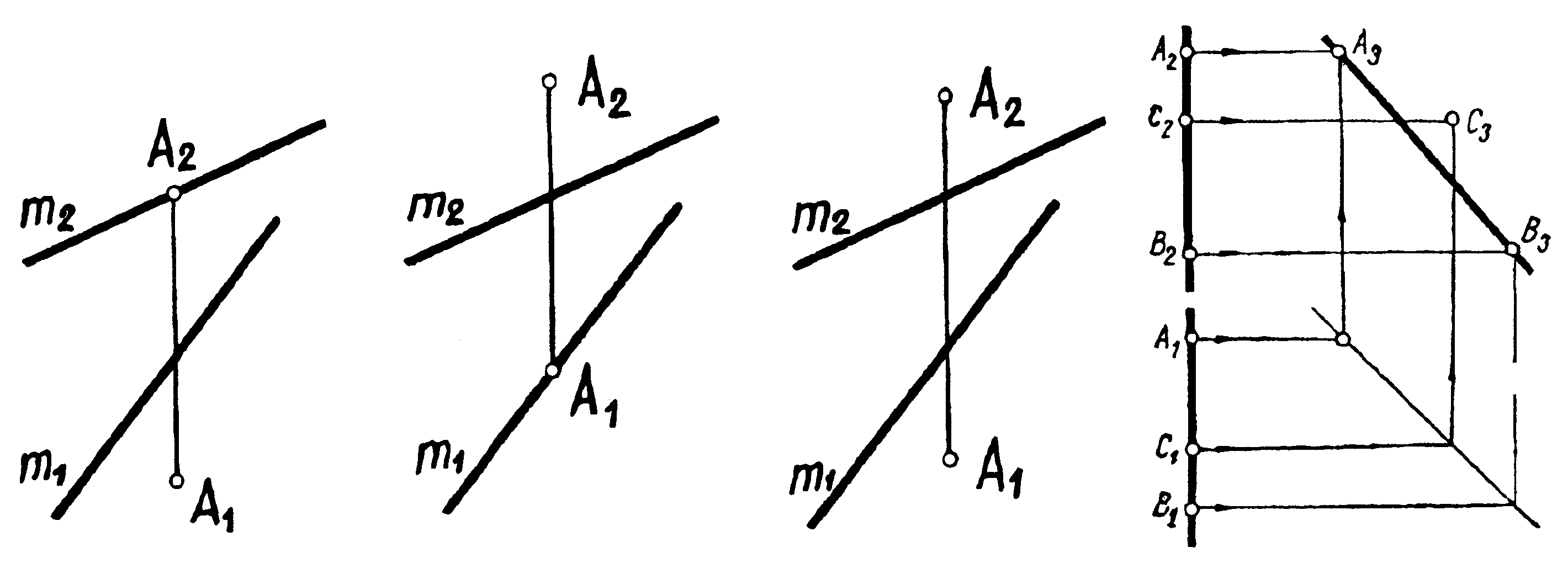
|
| Рисунок 3.2 Рисунок 3.3 Рисунок 3.4 Рисунок 3.5 |
Таблиця 3.2 – Відповіді на запитання 3.3
| Рисунок | Відповідь про взаємне розташування заданої точки і прямої |
| 3.2 | |
| 3.3 | |
| 3.4 | |
| 3.5 |
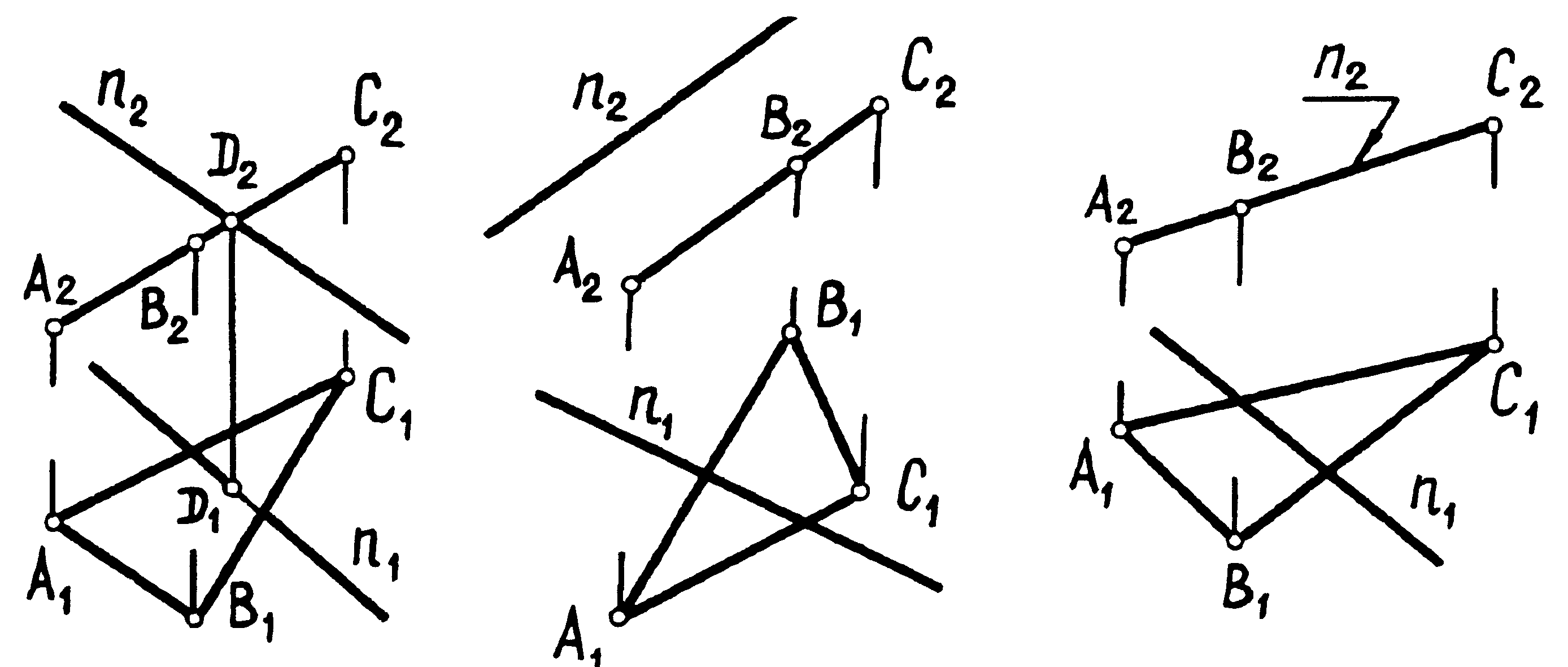
3.4 За заданими епюрами двох прямих (рисунки 3.6; 3.7; 3.8) визначити їх взаємне розташування. Відповіді наведіть у таблиці 3.3.
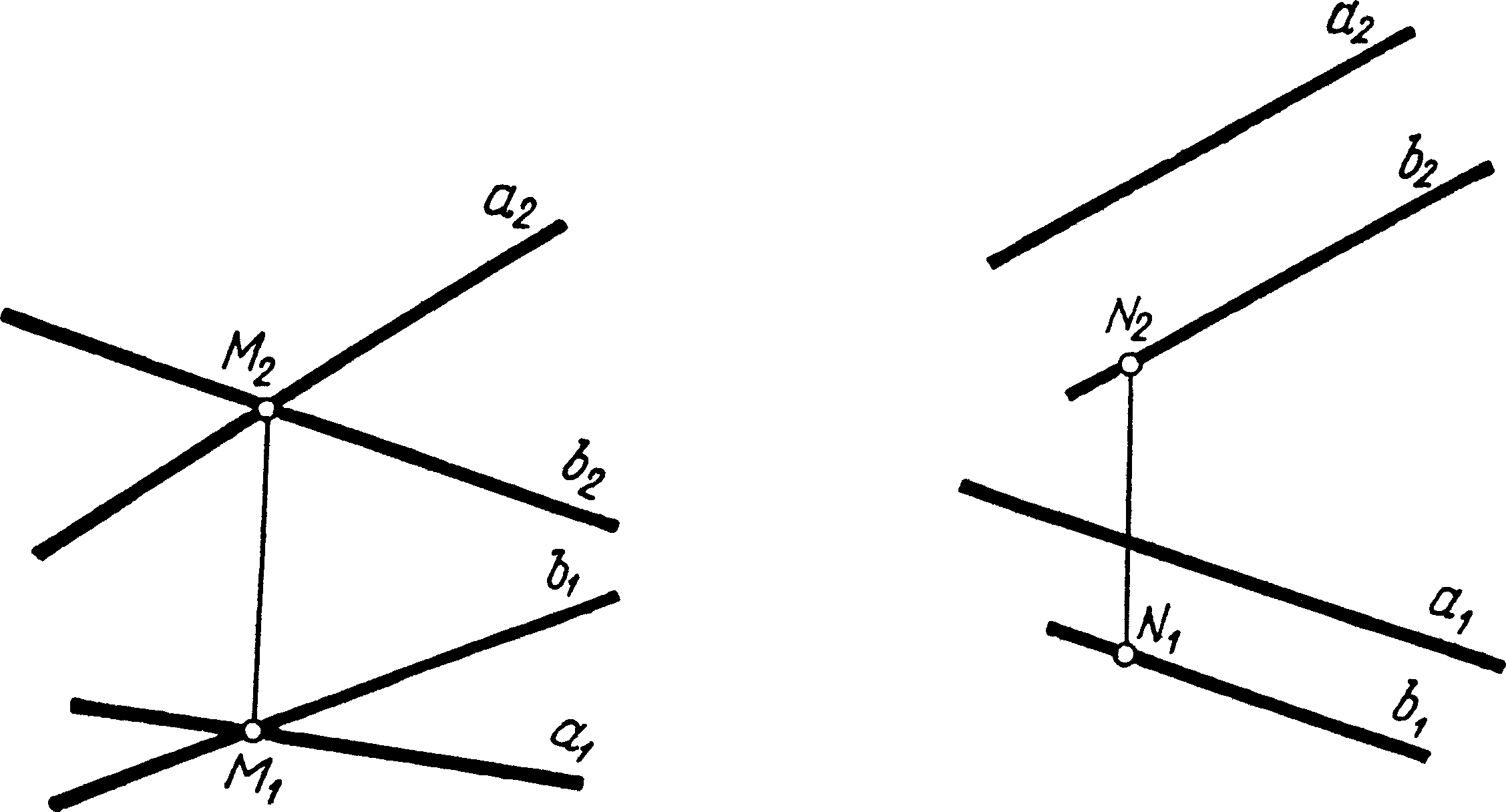  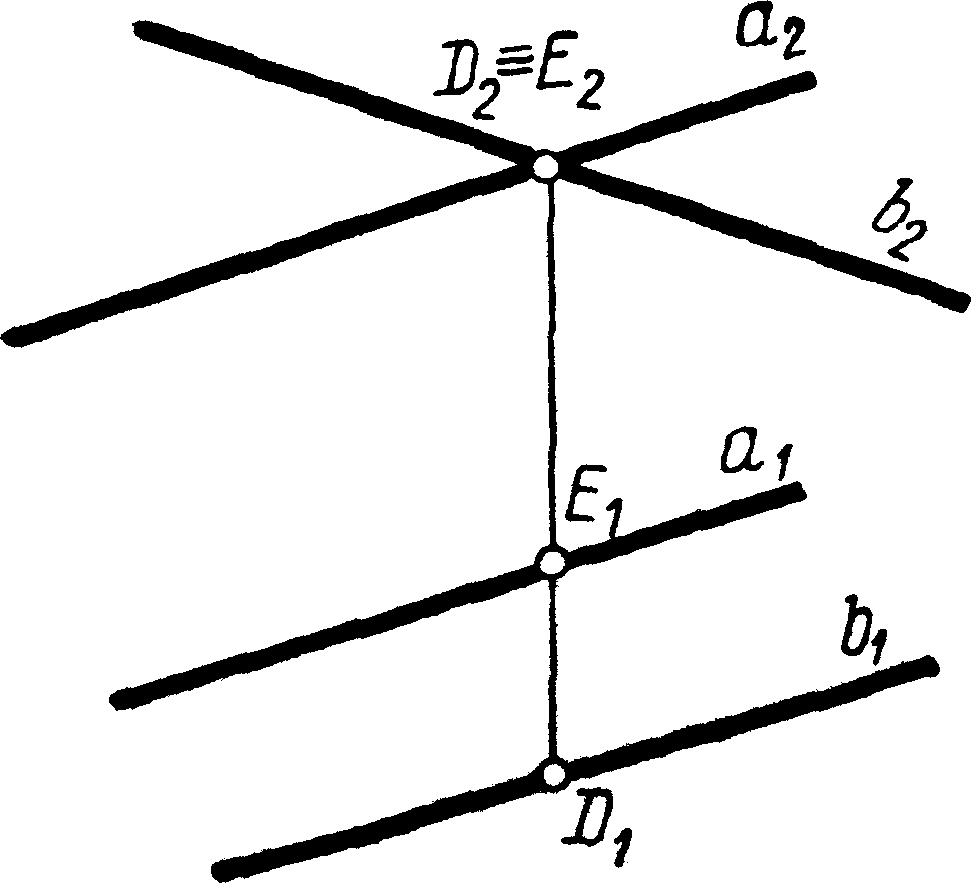
|
| Рисунок 3.6 Рисунок 3.7 Рисунок 3.8 |
Таблиця 3.3 – Відповіді на запитання 3.4
| Рисунок | Відповідь про взаємне розташування двох прямих |
| 3.6 | |
| 3.7 | |
| 3.8 |
3.5 Запишіть теорему про проекціювання прямого кута, що утворений двома прямими, які перетинаються між собою.
Теорема про проекціювання прямого кута. ________________________________
__________________________________________________________________________________________________________________________________________________________
3.6 За заданими епюрами прямої і площини (рисунки 3.9; 3.10; 3.11) визначити їх взаємне розташування. Відповіді наведіть у таблиці 3.4.
|
| Рисунок 3.9 Рисунок 3.10 Рисунок 3.11 |
Таблиця 3.4 – Відповіді на запитання 3.6
| Рисунок | Відповідь про взаємне розташування прямої і площини |
| 3.9 | |
| 3.10 | |
| 3.11 |
3.7 За даними, що наведені на рисунку 3.12 наведіть алгоритм побудови точки перетину прямої з площиною.
3.8 За наведеними аксонометричними рисунками 3.13 і 3.14, що наочно демонструють алгоритм побудови лінії перетину двох площин, навести його для випадку її побудови для розв’язаної вже задачі на рисунку 3.15. Алгоритм наведіть для побудови спільних двох точок 3 і 6, що визначають спільну лінію перетину заданих площин (3 - 6).
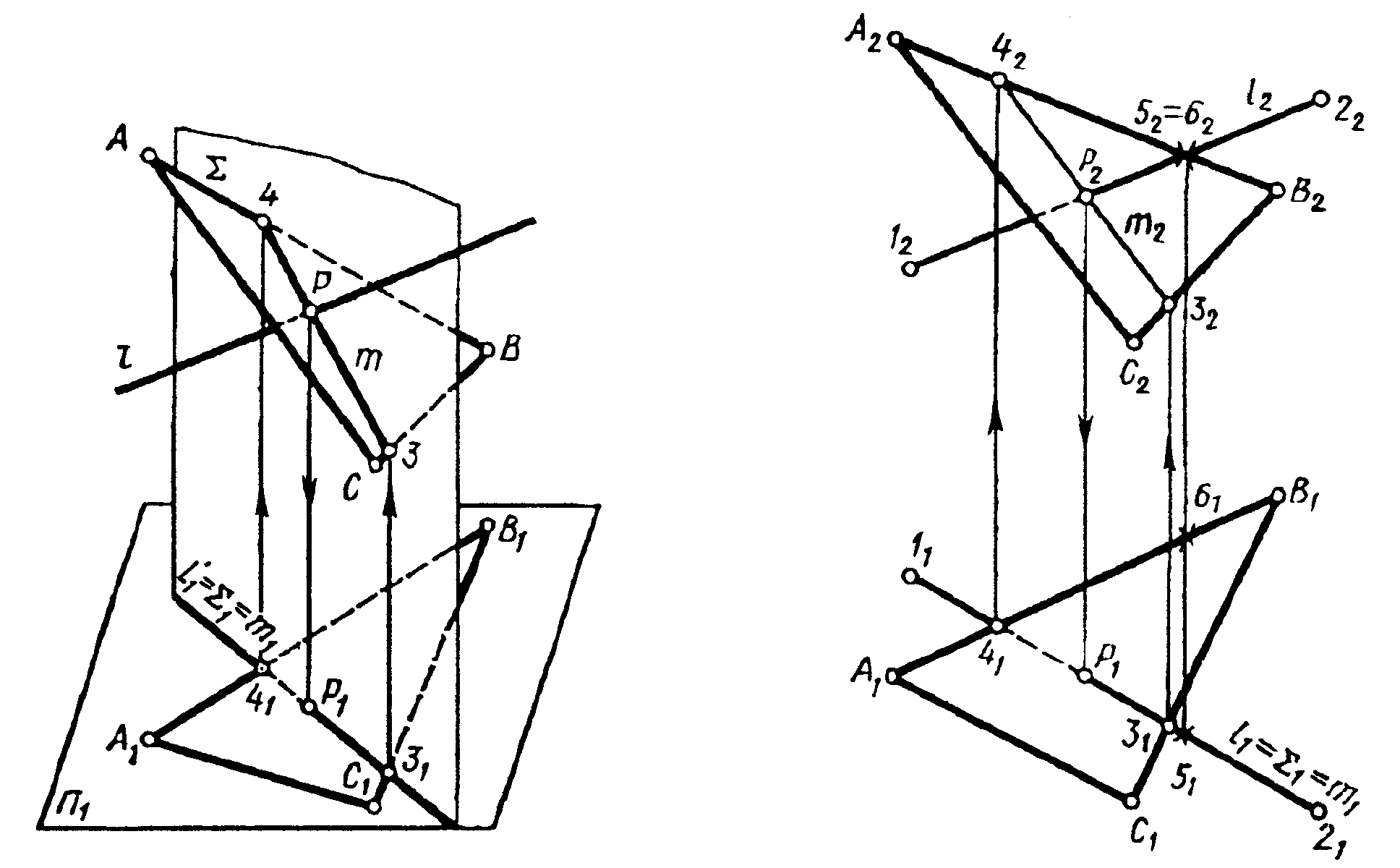
|
| а) б) Рисунок 3.12 – Побудова точки перетину прямої з площиною загального положення: а) наочне зображення; б) на епюрі |
Алгоритм побудови точки перетину прямої з площиною складається з таких кроків:
1) __________________________________________________________________
2) __________________________________________________________________
__________________________________________________________________________
__________________________________________________________________________
__________________________________________________________________________
3) __________________________________________________________________
__________________________________________________________________________.
| Робота на занятті: РОЗВЯЗОК ВПРАВ НА ПЕРЕТИН ПРЯМОЇ З ПЛОЩИНОЮ |
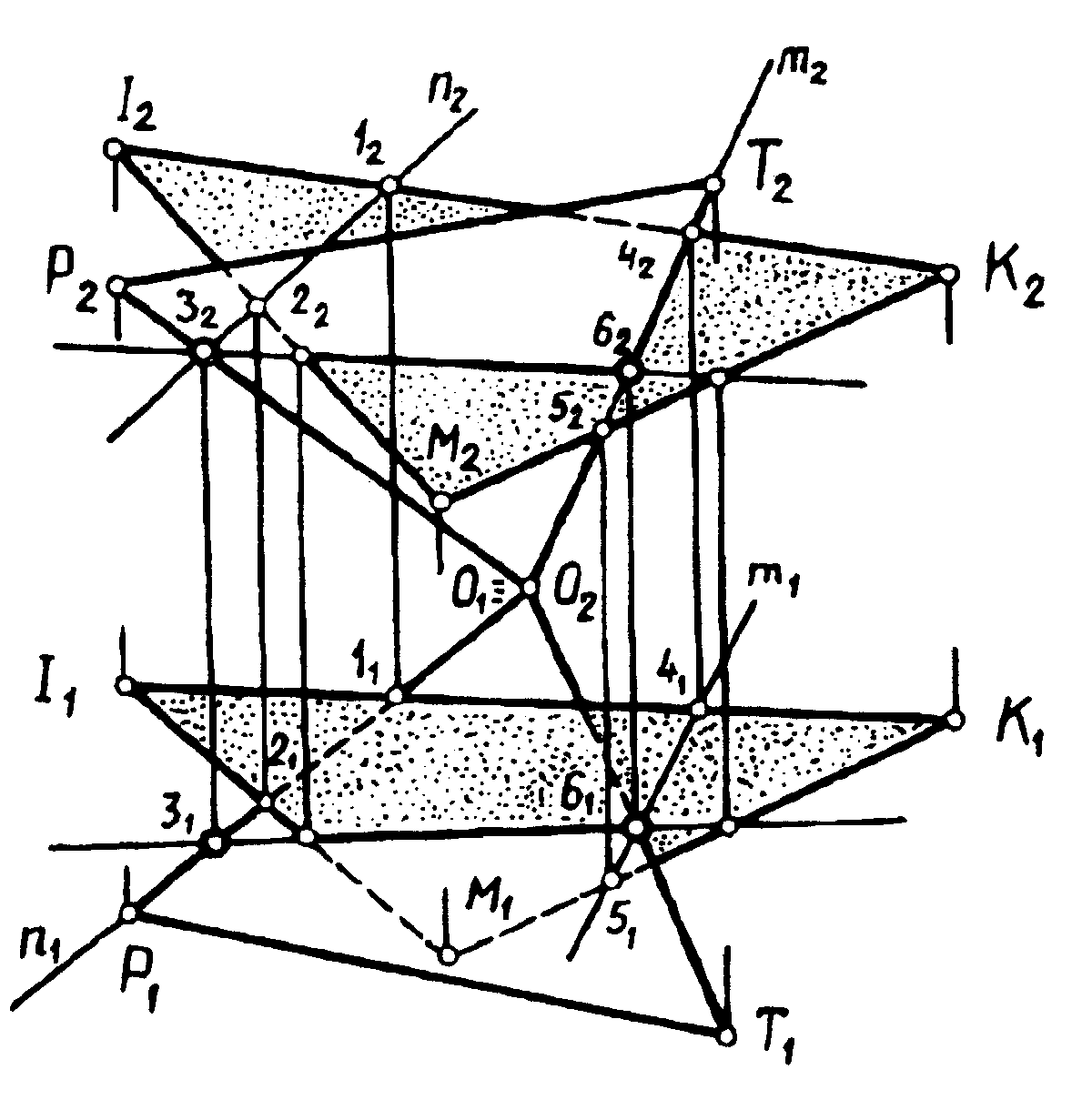
|
| Рисунок 3.13 – Побудова лінії перетину двох площин |
Дата: 2018-12-21, просмотров: 426.