Эта работа выполняется только в случае соответствия результатов расчёта требованиям, предъявляемым к качеству обработки, оговоренному в п. 2.3.5.
Поправки в приращения координат определяют по формулам:
vхi = – 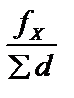 ´ di vyi = –
´ di vyi = – 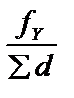 ´ di (27)
´ di (27)
где fx и fy – невязки в приращениях координат, м;
åd - периметр теодолитного хода, м;
di - горизонтальное проложение, по которому вычислено i-е приращение координат.
Из формулы (27) следует, что величина поправки распределяется по приращениям координат пропорционально величинам горизонтальных проложений и со знаком, обратным знаку невязки.
Величину поправки следует округлять до 0,01 м и подписать ее значение над вычисленным приращением координат (табл. 2).
Необходимо обеспечить выполнение следующих равенств:
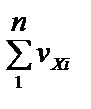 = – fx
= – fx 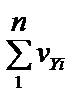 = – fy (28)
= – fy (28)
В результате округления равенства (3.28) могут не выполняться на 0,01 - 0,02 м. В этом случае производят корректировку величин поправок: в случае åvx,y > fx,y уменьшают на 0.01 м поправки, полученные по меньшим горизонтальным проложениям; в случае åvx,y < fx,y увеличивают на 0,01 м поправки, полученные по большим горизонтальным проложениям.
Исправление приращений координат выполняют алгебраическим суммированием с учетом величины и знака приращения координат и учётом величины и знака его поправки по формулам:
DХ1 испр = DХ1 выч + v x1 DY1 испр = DY1 выч + vy1 (29)
DХ2 испр = DХ2 выч + v x2 DY2 испр = DY2 выч + v y2 и т.д.
Контролем исправления приращений координат является выполнение условия (для замкнутого теодолитного хода):
åDХ испр = åDХ теор = 0 (30)
åDY испр = åDY теор = 0
Если условие (30) не выполнено, то:
1. Проверьте знаки невязок fx и fy.
2. Проверьте выполнение условия (28).
Таблица 2. ВЕДОМОСТЬ ВЫЧИСЛЕНИЯ КООРДИНАТ ТОЧЕК ТЕОДОЛИТНОГО ХОДА
| №№ точек | Горизонтальные углы b | Дирекционные углы a | Горизонтальное проложение d, м | Приращения координат | Координаты точек | №№ точек | ||||||
| вычисленные | исправленные | |||||||||||
| измер. | исправл. | DX | DY | DX | DY | X | Y | |||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
| В | 247° 30,9¢ |
|
|
|
|
| 4947,19 | 5204,81 | В | |||
| А | прим. g1 = 157° 18,4¢ | 4021,54 | 2968,42 | А | ||||||||
| 224° 49,3¢ |
|
|
|
|
| |||||||
| 1 |
|
|
|
| 1 | |||||||
|
|
|
|
|
|
| |||||||
| С |
|
| 2424,76 | 4251,08 | С | |||||||
| 321° 13,5¢ |
|
|
|
|
| |||||||
| А | прим. g2 = 83° 32,2¢ | 4021,54 | 2968,42 | А | ||||||||
| 224° 48,7¢ |
|
|
|
|
| |||||||
| 1 |
|
|
|
| 1 | |||||||
|
|
|
|
|
|
| |||||||
| А | – 0,2¢ 87° 19,4¢ |
87° 19,2¢ | 4021,54 | 2968,42 | А | |||||||
| 224° 49,0¢ | 69,24 | + 0,03 – 49,12 | +0,01 – 48,80 |
– 49,09 |
– 48,79 | |||||||
| 1 | – 0,3¢ 95° 48,7¢ |
95° 48,4¢ | 3972,45 | 2919,63 | 1 | |||||||
| 309° 00,6¢ | 82,49 | + 0,03 + 51,92 | +0,01 – 64,10 |
+ 51,95 |
– 64,09 | |||||||
| 2 | – 0,2¢ 101° 56,0¢ |
101° 55,8¢ | 4024,40 | 2855,54 | 2 | |||||||
| 27° 04,8¢ | 76,15 | + 0,03 + 67,80 | +0,01 + 34,67 |
+ 67,83 |
+ 34,68 | |||||||
| 3 | – 0,2¢ 74° 56,8¢ |
74° 56,6¢ | 4092,23 | 2890,22 | 3 | |||||||
| 132° 08,2¢ | 105,43 | + 0,04 – 70,73 | +0,02 + 78,18 |
– 70,69 |
+ 78,20 | |||||||
| А |
|
| 4021,54 | 2968,42 | А | |||||||
| 224° 49,0¢ |
|
|
|
|
| |||||||
| 1 | 1 | |||||||||||
Sbизм = 360° 00,9¢ Sbизм = 360° 00,9¢ Sd = 333,31 fX = – 0,13 fY = – 0,15 SDX = 0 SDY = 0
Sbтеор = 360° 00,9¢ fабс = 0,139
fb = + 0,9¢ f b доп = ± 2,0¢ fотн = 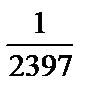 <
< 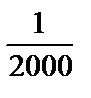
nb = – 0,2¢ в три угла, – 0,3¢ в один угол
3. Проверьте знаки поправок. Знаки поправок должны быть обратными знаку невязки.
4. Проверьте правильность суммирования по формуле (29) с учетом знаков приращений координат и их поправок.
При выполнении условия (30) вычисляют координаты точек теодолитного хода последовательно по движению в прямом (по ходу часовой стрелки) направлении:
Х1 = ХА исх + DХ1 испр Y1 = YА исх + DY1 испр
Х2 = Х1 + DХ2 испр Y1 = Y1 + DY2 испр (31)
Х3 = Х2 + DХ3 испр Y1 = Y2 + DY3 испр
Контрольным вычислением является определение координат точки А при замыкании по ходу через точку 3:
ХА контр = Х3 + DХА испр YА контр = Y3 + DYА испр (32)
При этом должно быть выполнено равенство:
ХА контр = ХА исх YА контр = YА исх (33)
Если равенство (33) не выполняется, то:
1. Еще раз посмотрите, выполнилось ли у Вас условие (30).
2. Проверьте, правильно ли Вы учитывали значения и знаки исправленных приращений координат при суммировании по формулам (31) и (32).
Если у Вас что-то снова не получается, посмотрите ниже пример обработки для вар. № А.
Пример.
Исправление приращений координат и вычисление координат
vx1 = – 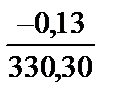 ´69,24 = +0,027=+0,03; vy1 = –
´69,24 = +0,027=+0,03; vy1 = – 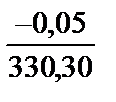 ´69,24 = +0,010=+0,01
´69,24 = +0,010=+0,01
vx2 = – 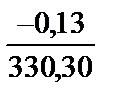 ´82,49 = +0,032=+0,03; vy2 = –
´82,49 = +0,032=+0,03; vy2 = – 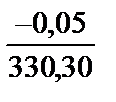 ´82,49 = +0,012=+0,01
´82,49 = +0,012=+0,01
vx3 = + 0,03 vy3 = +0,01
vxA = + 0,04 vyA = +0,02
åvx = +0,13 = – fx (= – 0,13) åvy = +0,05 = – fy (= – 0,05)
Условие (28) выполнено
DХ1 испр = – 49,12 + 0,03 = – 49,09; DY1 испр = – 48,80 + 0,01 = – 48,79
DХ2 испр = +51,92 + 0,03 = +51,95; DY2 испр = – 64,10 + 0,01 = – 64,09
DХ3 испр = +67,80 + 0,03 = +67,83; DY3 испр = +34,67 + 0,01 = +34,68
DХА испр = - 70,73 + 0,04 = -70,69; DYА испр = +78,18 + 0,02 = +78,20
åDХ испр = 0 åDY испр = 0
Условие (3.30) выполнено
Х1 = 4021,54 - 49,09 = 3972,45 Y1 = 2968,42 - 48,79 = 2919,63
Х2 = 3972,45 + 51,95 = 4024,40 Y1 = 2919,63 - 64,09 = 2855,54
Х3 = 4024,40 + 67,83 = 4092,23 Y1 = 2855,54 + 34,68 = 2890,22
Контрольное вычисление:
ХА контр = 4092,23 - 70,69 = 4021,54 Y1 = 2890,22 + 78,20 = 2968,42
Условие (33) выполнено.
Обработка ведомости высот
Образец ведомости высот и пример ее обработки для варианта А приведены в табл. 3.
Таблица 3. ВЕДОМОСТЬ ВЫСОТ ТОЧЕК ТЕОДОЛИТНОГО ХОДА
| №№ точки | Горизонтальное проложение, м | Угол наклона в прямом направлении | Превышения | Высоты точек Н, м | №№ точки | |
| вычисленные | исправленные | |||||
| А | – 0,01 | 64,33 | А | |||
| 69,24 | + 4° 25,6¢ | + 5,36 | + 5,35 | |||
| 1 | – 0,01 | 69,68 | 1 | |||
| 82,49 | + 1° 19,2¢ | + 1,90 | + 1,89 | |||
| 2 | – 0,01 | 71,57 | 2 | |||
| 76,15 | – 5° 33,5¢ | – 7,41 | – 7,42 | |||
| 3 | – 0,01 | 64,15 | 3 | |||
| 105,43 | + 0° 06,2¢ | + 0,19 | + 0,18 | |||
| А | 64,33 | А | ||||
fh = + 0,04 м Shиспр = 0
fh доп = ± 0,067 м
Исходными данными в ведомости высот являются (выделено):
· горизонтальные проложения (см. ведомость координат);
· углы наклона (см. приложение 3);
· абсолютная высота точки А (см. приложение 2).
Дата: 2018-12-21, просмотров: 1105.