Азимутальная привязка теодолитного хода
Для азимутальной привязки необходимо знать величины дирекционных углов aВА и aСА, получить которые можно из решения обратной геодезической задачи по координатам Х и Y точек А, В и С.
Дирекционный угол – это горизонтальный угол, отсчитываемый от северного направления осевого меридиана (либо линии, параллельной ему) по часовой стрелке до направления линии в данной точке.
Значение дирекционного угла должно находится в пределах от 0° до 360°
Порядок решения обратной геодезической задачи следующий:
a) Вычислить приращения координат DХ и DY для точки А по отношению к точкам В и С:
DХА(В) = ХА - ХВ DХА(С) = ХА - ХС
DYА(В) = YА - YВ DYА(C) = YА - YC (1)
где ХА, YА, ХВ, YВ, ХС и YС - прямоугольные координаты точек А, В и С
(см. приложение 1);
b) По знакам приращений координат, пользуясь табл. 1, определить четверть и формулу для расчёта дирекционного угла по значению румба (r) данной линии.
Таблица 1
| DХ | + | – | – | + |
| DY | + | + | – | – |
| Четверть | I (СВ) | II (ЮВ) | III (ЮЗ) | IV (СЗ) |
| a = f (r) | a = r | a = 180°– r | a = 180°+ r | a = 360°– r |
c) Вычислить значение румба линии:
r = arctg 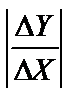 (2)
(2)
d) Вычислить значение дирекционного угла линии:
a = f (r) - по табл. 1 (3)
Значение дирекционного угла необходимо округлить до 0,1¢.
Пример
Решение обратной геодезической задачи (вариант А)
aВА
DХА(В) = 4021,54 – 4947,19 = – 925,65 м
DYА(В) = 2968,42 – 5204,81 = – 2236,39 м
III четверть (ЮЗ); a = 180°+ r
rВА = arctg 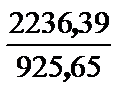 = arctg 2,416021 = 67° 30,9¢
= arctg 2,416021 = 67° 30,9¢
aВА = 180° 00,0¢ + 67° 30,9¢ = 247° 30,9¢
aСА
DХА(С) = 4021,54 – 2424,76 = + 1596,78 м
DYА(С) = 2968,42 – 4251,08 = – 1282,66 м
IV четверть (СЗ); a = 360°– r
rСА = arctg 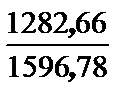 = arctg 0,803279 = 38° 46,5¢
= arctg 0,803279 = 38° 46,5¢
aСА = 360° 00,0¢ – 38° 46,5¢ = 321° 13,5¢
В ведомость координат внести исходные данные из приложений 2 и 3 и результаты решения обратной геодезической задачи.
Посмотрите порядок записи в ведомость координат (табл. 2).
Азимутальная привязка линии А1 теодолитного хода заключается в передаче дирекционных углов направлений ВА и СА на линию А1 по формулам:
aА1(ВА) = aВА + 180° + g1
a А1(СА) = aСА + 180° + g2 (4)
(Для левых по ходу примычных углов g1 и g2).
Значения полученных дирекционных углов aА1(ВА) и aА1(СА) не должны отличаться друг от друга более, чем на 1¢:

 aА1(ВА) - aА1(СА)
aА1(ВА) - aА1(СА) 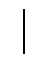 £ 1¢ (5)
£ 1¢ (5)
Величину дирекционного угла следует приводить к полному кругу от 0° до 360°
Если a > 360°, то его необходимо уменьшить на 360°. Если a < 0°, то его необходимо увеличить на 360°.
Если у Вас не выполняется условие (3.5), то:
1. Проверьте исходные данные: Х, Y, g1, g2.
2. Проверьте правильность знаков DХ и DY и выбора формулы расчёта дирекционного угла по значению румба.
3. Проверьте правильность вычисления r., например, r = 46,237568°
При этом 0,237568° ´ 60 = 14,254¢ = 14,3¢
Следовательно, r = 46,237568° = 46° 14,3¢
4. При использовании в вычислениях углов, заданных в градусах, минутах и долях минуты, следует не забывать, что 1° = 60¢.
При выполнении условия (3.5) вычисляют среднее арифметическое значение дирекционного угла
aА1 = 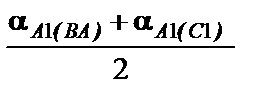 (6)
(6)
Результаты расчётов заносят в табл. 2.
Пример
Азимутальная привязка линии теодолитного хода
aА1(ВА) = 247° 30,9¢ + 180° + 157° 18,4¢ = 584° 49,3¢ = 224° 49,3¢
aА1(СА) = 321° 13,5¢ + 180° + 83° 35,2¢ = 584° 48,7¢ = 224° 48,7¢
Поскольку 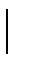 224° 49,3¢ - 224° 48,7¢ 224° 49,3¢ - 224° 48,7¢ 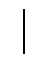 = 0,6¢ < 1¢, то условие (5) выполнено.
aА1 = = 0,6¢ < 1¢, то условие (5) выполнено.
aА1 = 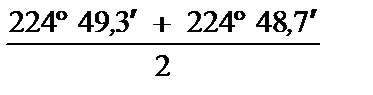 = 224° 49,0¢.
Посмотрите форму записи результатов в ведомости координат. = 224° 49,0¢.
Посмотрите форму записи результатов в ведомости координат.
|
Дата: 2018-12-21, просмотров: 726.