Приращения координат вычисляют по формулам:

DХ = d ´ cosa                                

DY = d ´ sina                                      (19)

где d – горизонтальное проложение линии;

a – дирекционный угол той же линии по ходу часовой стрелки.

Так, в принятой системе обозначений для данного теодолитного хода,

DХ₁ = d_А1 ´ cosa_А1            DY₁ = d _А1 ´ sina_А1       

DХ₂ = d₁₂ ´ cosa₁₂                 DY₂ = d ₁₂ ´ sina₁₂

DХ₃ = d₂₃ ´ cosa₂₃                 DY₃ = d ₂₃ ´ sina₂₃       (20)

DХ_А = d_3А ´ cosa_3А           DY_А = d _3А ´ sina_3А

Для замкнутого теодолитного хода суммы приращений координат должны быть равны нулю:

åDХ_теор. = 0                       åDY_теор. = 0              (21)

Из-за ошибок в измерении горизонтальных углов, как это следовало из обработки угловых измерений, ошибок в определении горизонтальных проложений, связанных с ошибками в измерении наклонных расстояний и углов наклона, суммы приращений координат могут оказаться не равными нулю, а равными какой-либо величине

f_x = åDХ_выч.              f_y = åDY_выч.                                 (22)

называемыми невязками в приращениях координат.

Геометрический смысл невязок f_x и f_y в приращениях координат поясняется на рис. 2

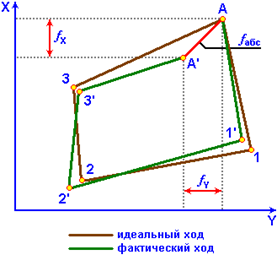
Рисунок 2. Невязки в приращениях координат

Точки А, 1, 2 и 3 закрепленные на местности образуют идеальный теодолитный ход, не содержащий погрешностей. В результате измерений ошибки в значениях углов и расстояний приводят к тому, что при движении, например, из т. А в т.1 измеренное положение т. 1 не совпадает в общем случае с идеальным положением т. 1. И так по всему ходу. И в конце хода образуется его незамыкание на исходную точку А.

Величина незамыкания f_абс называется абсолютной невязкой хода.

Величину абсолютной невязки хода легко получить по величинам ее проекций на координатные оси:

f_абс = 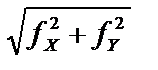                                                  (23)

Для сравнительной оценки точности теодолитного хода вычисляют относительную невязку:

f_отн = 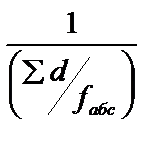 = 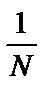,                                        (3.24)

где åd - периметр теодолитного хода.

Контролем качества теодолитного хода является выполнение условия:

f_отн £ f_{отн допустимая}                                             (25)

В задании f_{отн доп} = .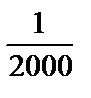

Если условие (25) не выполняется, то:

1. Проверить правильность вычисления f_x и f_y.

2. Проверить знаки приращения координат.

3. Проверить дальнейшие арифметические действия

Предварительная оценка ошибки в вычислениях может быть выполнена по величине дирекционного угла абсолютной невязки теодолитного хода. Определить величину дирекционного угла можно из решения обратной геодезической задачи. (см. п. 2.3.1). При этом

rf_абс = arctg 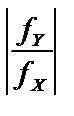                                                        (26)

По знакам f_x и f_y определяют четверть, формулу определения дирекционного угла af_абс и вычисляют его значение.

Наиболее вероятна ошибка в линиях, дирекционный угол которых близок к af_абс и af_абс ±180°.

Пример Вычисление приращений координат и оценка точности теодолитного хода DХ1 = 69,24´cos224° 49,0¢ = -49,12; DY1 = 69,24´sin224° 49,0¢ = -48,80 DХ2 = 82,49´cos309° 00,6¢ = +51,92 DY2 = 82,49´sin309° 00,6¢ = -64,10 DХ3 = 76,15´cos 27° 04,8¢ = +67,80 DY3 = 76,15´sin 27° 04,8¢ = +34,67 DХА = 105,43´cos132°08,2¢= -70,73 DYА = 05,43´sin132°08,2¢=+78,18 åDХ = fx = - 0,13                åDY = fy = - 0,05 fабс = 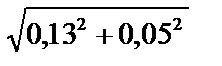 = 0,139 м åd = 333,30 м fотн = 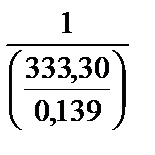=  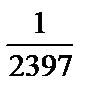=  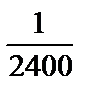< 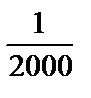Условие (25) выполнено.   Предположим, что условие (25) не выполнено. Тогда: rfабс = arctg 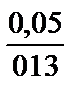 @ 21° afабс = (III четверть (ЮЗ)) = 180° +21° @ 201°. Т.е., см. табл. 2, наиболее вероятна ошибка в линии 2-3 или в линии А-1, поскольку afабс @ 201°, afабс ± 180° @21° и a23 @ 27°, а aА1 @ 224°. Посмотрите форму записи результатов в ведомости координат (табл. 2).