Логическая автономность математики не означает автономности функ­циональной: математика развивается не для самой себя, а в ориентации на запросы научного знания. Особенности развития математического знания могут быть в полной мере поняты только с учетом этой внешней связи. Развитие математики в Новое время, конечно, не было автоном­ным, оно было продиктовано развитием техники, промышленности и теоретического естествознания. Развитие математического анализа, как известно, самым тесным образом связано с проблемами механики и те­оретической физики в целом. Расширяющееся приложение математики к нематематическим наукам составляет суть процесса, который мы на­зываем математизацией знания.

Общая схема математизации знания предельно проста и сводится в ко­нечном итоге к интерпретации математической теории через понятия тео­рии содержательной или, если идти со стороны содержания, к выявлению математических связей и отношений, отражающих определенные аспекты реальности, зафиксированные в содержательной теории. Классическим примером эффективной математизации является применение математики к проблемам механики. Это применение основано на структурном тожде­стве математических и содержательных законов. Мы замечаем, что если дана формула, выражающая зависимость пройденного пути от времени, то производная от этого выражения по времени будет соответствовать вели­чине скорости движения, а вторая производная — величине ускорения. Это замечательное соответствие математических и физических понятий позволяет все понятия и связи механики записать в виде математических функций и установить между этими функциями четкие, чисто математиче­ские связи. Проблемы механики переводятся таким образом в чисто мате­матическую плоскость, точно таким же образом, как проблемы геометрии были в свое время преобразованы Декартом в проблемы алгебры благода­ря выявлению соответствия между геометрическими и алгебраическими понятиями. В процессе математизации, однако, математическая теория интерпретируется не в понятиях другой математической теории, а в поня­тиях теории содержательной.

Важно заметить, что процесс математизации зависит как от развития математики, так и от зрелости содержательной науки. Математизация механики не состоялась бы, если бы не была разработана в достаточной мере теория дифференциального исчисления, но, с другой стороны, она не состоялась бы без ясного определения таких понятий, как масса, ус­корение, количество движения и т.д. Без этих понятий мы не сформули­ровали бы в ясной форме законов механики и не смогли бы выявить их

58                                       1. Философские проблемы математики

собственно формальную или математическую структуру. Математика применяется к тем областям знания, которые достигли достаточно вы­сокой степени структуризации своего объекта. Практика показывает, что далеко не все науки способны к ясной структуризации предмета, обеспечивающей использование математического метода.

Пример механики позволяет нам ввести важное понятие классичес­кой или полной математизации. Мы будем называть математизацию те­ории полной,если:

• качественные характеристики объектов теории допускают адекват­ную меру;

• все основные понятия и принципы теории поддаются выражению в математических понятиях;

• математическая теория позволяет осуществить достаточно точные предсказания в области действия (приложения) этой теории.

Очевидно, что классическая механика уже в XVIII в. достигла степени полной математизации. Не только исходные понятия теории, какими явля­ются сила, масса и ускорение, определены через строгие формальные отно­шения к другим понятиям, но и все производные понятия выведены на ос­нове исходных. То же самое относится и к единицам измерения. Исходные величины, а именно величины массы, длины и времени определены через общезначимые эталоны, производные же величины — через исходные на основе теоретических связей между ними. Полная математизация имеет место также и в других физических теориях, таких, как термодинамика, электродинамика, квантовая механика и теория поля. Принципы этих тео­рий имеют адекватное математическое представление, все их внутренние величины определены через исходные, и эти теории обладают высокой адекватностью отражения реальности в том смысле, что они способны да­вать точные предсказания и описания процессов, протекающих в природе и в различного рода технических устройствах.

Для математизации научной теории принципиально важным являет­ся допустимый в ней способ измерения величин. Мы должны различать адекватные и неадекватные меры. Меру величины можно назвать адек­ватной, если мы убеждены, что большей величине соответствует боль­шая мера, равным величинам — равные меры и при увеличении величи­ны в некоторое число раз ее мера увеличивается в то же самое число раз. Адекватная мера предполагает наличие способа измерения, прежде все­го, единиц измерения, зафиксированных в виде устойчивых эталонов. Все физические величины обладают в этом смысле адекватной мерой, поскольку они выражаются в конечном итоге через меры длины, массы и времени, которые фиксируются с предельной определенностью.

Основной недостаток теорий за пределами физики заключается в от­сутствии адекватных мер, и поэтому приходится прибегать, как правило, к условным мерам, которые мало пригодны для точного выражения функ-

1.6. Фшюсофско-методологические и исторические проблемы...                               59

циональных связей. У нас нет адекватной меры для определения величи­ны грамотности общества, и мы вынуждены пользоваться для выражения ее такими условными характеристиками, как среднее число лет, которое затрачивается в данной стране на обучение ребенка, уровень финансиро­вания системы образования и т.д. Конечно, мы имеем качественные при­знаки, позволяющие отличить развитую экономику от менее развитой, но не существует единого показателя, позволяющего дать точное количест­венное выражение качества экономической системы. Условность измере­ния ведет к условности устанавливаемых функциональных связей и к ог­раничению теоретического анализа в смысле точности предсказаний.

Существенное отличие современной математизации от классической состоит в том, что она не является полной. Она фрагментарна в том смыс­ле, что математическому моделированию поддаются лишь некоторые ча­стные процессы, исследуемые теорией, но не теория в целом. Мы строим здесь модель для некоторого процесса, не имея математического представ­ления об основных понятиях и принципах теории. Примером такой час­тичной математизации является математическая модель сосуществования хищников и жертв в биоценозе, предложенная В. Вольтерра. Интуитивно ясно, что увеличение числа зайцев в лесу как потенциальных жертв ведет к увеличению числа волков как особей, потребляющих зайцев в пищу, и что слишком бурное размножение волков должно привести к уменьшению числа зайцев и, в конце концов, к сокращению числа волков. Намечается, таким образом, некоторое взаимодействие двух линий развития во време­ни. Эта ситуация может быть записана в следующих уравнениях:

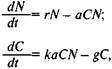
где N — число жертв, С— число хищников, а, г, к, g — коэффициенты, ха­рактеризующие взаимодействие хищников и жертв, устанавливаемые на основе опыта. Эти уравнения допускают уточнение и в принципе могут служить для предсказания тенденций увеличения или уменьшения основ­ных видов в биоценозе. Известно, что математическое моделирование процессов в биоценозе дает неплохие результаты в прогнозах вылова раз­личных пород рыб по сезонам в замкнутых водных бассейнах¹.

Этот пример показывает особенности неклассической (фрагментар­ной) математизации. Такая математизация не захватывает принципов на-

Детальный анализ уравнений Вольтерра см.: Тутубалин В.Н., Барабашева Ю.М., Гри­ горян А.А., Девяткова Г.Н., Угер Е.Г. Математическое моделирование в экологии. Истори-ко-методологический анализ. М, 1999.

60                                        1. Философские проблемы математики

уки в целом, она относится исключительно к некоторым выделенным, изолированным фрагментам. Важно также то, что такого рода математиза­ция не опирается на адекватные меры и не обеспечивает точного предска­зания. Математизация знания за пределами физики является фрагментар­ной и неточной из-за отсутствия адекватно измеряемых величин. Имеются серьезные доводы в пользу того, что математизация за пределами физики не имеет шансов стать полной и адекватной математизацией в определен­ном выше смысле. Ни одна гуманитарная наука, конечно, не может до­стичь такой законченной аксиоматической структуры изложения, кото­рую приобрела механика уже на ранней стадии своего развития. Опыт науки последних десятилетий показывает, однако, что несмотря на указан­ные недостатки фрагментарной математизации, она завоевывает все но­вые и новые области, демонстрируя таким образом свою полезность. Все говорит о том, что гуманитарные науки по мере своего развития будут тре­бовать все более широкого использования математических методов.

В философском плане основная проблема математизации состоит в прояснении ее онтологической основы, ее обусловленности сложностью предмета науки. История науки ясно показывает, что математической об­работке поддаются только те теории, в которых могут быть выявлены мо­дели, пригодные для количественной обработки и для определения в точ­ных понятиях. Математизация знания зависит, таким образом, в первую очередь от внутренних особенностей самого этого знания, от его способ­ности к внутренней определенности, от наличия в нем достаточно опре­деленных и вместе с тем достаточно содержательных схем. Научные тео­рии сильно различаются по своей способности к строгому определению понятий и в разной степени способны к представлению своих законов в математических понятиях. Проблема состоит в уяснении условий, обус­ловливающих возможность математизации знания, в установлении тре­бований, позволяющих понять возможную сферу эффективности матема­тического метода. В настоящее время мы не имеем здесь сколько-нибудь ясных представлений, и можно сказать, что существующая теория мате­матизации знания ограничивается покалишь анализом ее истории и срав­нением типов задач и используемого математического аппарата.

Современная математизация знания отличается от классической и в том смысле, что она тесно связана с развитием вычислительной техники и в этом плане может быть квалифицирована так же, как его компьюте­ризация. Это обстоятельство объясняется прежде всего тем, что модель­ный и приближенный характер современной математизации требует со­вершенствования (подгонки) модели к условиям реальности. Такого рода совершенствование модели не может быть достигнуто средствами тради­ционного теоретического анализа, но во многих случаях легко достигает­ся на основе вычислительного эксперимента. Можно сказать, что вычис­лительный эксперимент позволяет преодолеть самый существенный

1.6. Философско-методологические и исторические проблемы...                               61

недостаток фрагментарной математизации — отсутствие адекватных мер и точности предсказания. Известно, что достаточно точные модели пове­дения объектов могут быть построены и в тех случаях, где еще не достиг­нуто адекватного теоретического описания и даже нет ясного понимания процесса. Продвижение математических методов в психологию и гума­нитарные науки было бы невозможным, если бы мы должны были опи­раться здесь только на достигнутое теоретическое понимание процессов и на строгую дедукцию из принципов. Современная математизация об­ладает, таким образом, некоторой независимостью от теории, что являет­ся одним из ее преимуществ перед математизацией классической.

Для понимания математизации знания и общего механизма соотно­шения математики и опыта в процессе развития науки важно также по­яснить такие относящиеся к ней явления, как математическое предвос­хищение и математическая гипотеза. Явление математического предвосхищения состоит в применении к описанию реальности матема­тических понятий и теорий, созданных первоначально исключительно из теоретических соображений, без прямой связи с опытом. Так, мате­матическая теория групп, созданная Лежандром, Абелем и Галуа, нашла в прошлом столетии использование в квантовой механике и теории эле­ментарных частиц, а неевклидовы геометрии — в теории относительно­сти. Аналогичным образом обнаружилась тесная связь с опытом абст­рактных топологических пространств и даже закономерностей распределения простых чисел, которые открывались, конечно, без вся­кой связи с запросами теоретического естествознания. А. Эйнштейн в статье о Кеплере высказывал восхищение загадочной гармонией приро­ды и мысли, благодаря которой геометрические фигуры, придуманные древними, а именно эллипс и гипербола, нашли в Новое время реализа­цию в орбитах небесных тел¹. Н. Бурбаки также усматривает проблему в том, что некоторые аспекты экспериментальной действительности «как будто в результате предопределенности» укладываются в некоторые из существующих математических форм². Конечно, здесь не следует усма­тривать какой-либо мистики. Эти факты показывают, однако, наличие глубинных связей между развитием математики и опытных наук, кото­рые не сводятся к простому взаимовлиянию структур и которые нам предстоит еще понять в процессе методологического анализа.

Явление математической гипотезы состоит в том, что чисто формаль­ные, иногда даже непреднамеренные изменения математических урав­нений, описывающих определенные стороны реальности, приводят к закономерностям, описывающим другие стороны реальности или сущест-

' См.: Эйнштейн А. Физика и реальность. М., 1965. С. 109.

² См.: Бурбаки Н. Архитектура математики // Бурбаки Н. Очерки по истории матема­тики. М., 1963. С. 258.

62                                        1. Философские проблемы математики

венно расширяющим поле использования первоначальной теории¹. Впе­чатляющим примером такой формальной вариации является уравнение Шрёдингера, полученное в результате модификации классического волно­вого уравнения. Этот путь привел в конечном итоге к прояснению принци­пов квантовой механики и широкого поля ее приложений. Особенностью этого пути является то, что математический аппарат теории появляется раньше его адекватной содержательной интерпретации. Некоторые иссле­дователи методологии науки видят в этом новую форму взаимодействия между математикой и научной теорией, появившуюся в XX в., которая ха­рактеризуется тем, что математика начинает играть ведущую и решающую роль в становлении физической (содержательной) теории².

Математическая гипотеза родственна математическому предвосхище­нию, так как в том и другом случае речь идет об активной и опережающей роли математики в развитии содержательной теории. Но тут есть и сущест­венное различие: говоря о математическом предвосхищении, мы фиксиру­ем некоторого рода исторически реализующуюся тенденцию, способность математики готовить форму для новых физических теорий, в то время как в случае с математической гипотезой мы говорим о сознательном исполь­зовании этой особенности развития математики, т.е. о некотором методе, основанном на этом свойстве математической теории. Можно сказать, что математическая гипотеза является методологической реализацией, пред­восхищающей способности математического мышления.

Современная математизация знания в методологическом плане пред­ставляет собой сложное, противоречивое и во многих отношениях еще не вполне понятое явление. Мы ясно видим, что, хотя усложнение объекта исследования создает почти непреодолимые затруднения для математиче­ского представления теории, спрос на математику со стороны науки, в том числе и наук за пределами физики, постоянно растет. Вопрос о пер­спективах математизации знания, таким образом, остается открытым. Для понимания этих перспектив необходимо иметь более определенные знания об условиях применения математики к таким объектам, как объ­екты биологии, психологии и социальной науки. Достаточно полной ме­тодологической теории, отвечающей на эти вопросы, мы пока не имеем.

Вопросы для самопроверки

1. Что общего и в чем состоит существенное различие в подходе к методоло­гическим проблемам математики в рамках фундаменталистского и нефундамен­талистского направлений в современной философии математики?

¹ См.: Кузнецов И.В. Избранные труды по методологии физики. М., 1975. С. 85—101.

² См.: Визгин Вл.П. Проблемы взаимосвязи математики и физики. Историко-матема-
тические исследования. М., 1975. Вып. XX; Клайн М. Математика. Утрата определенности.
М., 1988. Гл. 13.

1.6. Философско-методологические и исторические проблемы...            63

2. В чем состоит особая роль геометрии как теоретической науки в становле­нии дедуктивной формы изложения математического знания?

3. Каким образом закономерности развития математики связаны с различи­ем теоретической и практической математики?

4. Укажите основные расхождения между эмпирическим и априористским истолкованием математических понятий.

5. Что значит обосновать математическую теорию с логицистской, интуици­онистской и формалистской точки зрения?

6. В чем состоят особенности современной математизации знания?

Темы рефератов

1. Место математики в культуре.

2. Абстракции и идеальные объекты в математике.

3. Взгляды математиков на методологические проблемы науки (Г. Кантор, Д. Гильтерт, А. Пуанкаре, Г. Вейль, Н.Н. Лузин, А.Н. Колмогоров, В.И. Арнольд, СП. Новиков).

4. Математика и физика в их историческом взаимодействии.

5. Логика и интуиция в математике.

6. Проблема бесконечности в математике.

7. Особенности развития математики.

8. Эмпиризм в философии математики.

9. Априористская концепция математики.

10. Аксиоматический метод в математике.

11. Математическое предвосхищение и математическая гипотеза.

12. Проблема обоснования математики.

13. Методологические особенности современной математизации знания.

14. Философские проблемы теории вероятностей.

15. Роль компьютеров в развитии современной математики.

16. Социокультурные концепции развития математики (работы К. Поппера, И. Лакатоса, Ф. Китчера, А.Г. Барабашева).

17. Развитие математики и проблемы математического образования (работы В.И. Арнольда, A.M. Абрамова, по колмогоровской реформе и др.).

Литература

Абрамов A. M. О педагогическом наследии А.Н. Колмогорова // УМН. 1988. Вып. 6. Т. 43. С. 39-74.

Арнольд В.И. Математическая дуэль вокруг Бурбаки // Вестник РАН. 2002. Т. 72. № 3.

Барабашев А.Г. Будущее математики. Методологические аспекты прогнози­рования. М., 1991.

Бурбаки Н. Очерки по истории математики. М., 1963.

Бычков С.Н. Египетская геометрия и греческая наука // Историко-математи-ческие исследования. Вторая серия. М., 2001. Вып. 6 (41).

64                             1. Философские проблемы математики

Бычков С.Н. Математика в историческом измерении // Вопросы истории ес­тествознания и техники. 2003. № 3.

ВолошиновА.В. Математика и искусство. М., 2000.

Григорян А.А. Закономерности и парадоксы развития теории вероятностей. Философско-методологический анализ. М., 2004.

Закономерности развития современной математики. М., 1987.

Казарян В.П., Лолаев Т.П. Математика и культура. М., 2004.

Кацивели Г. (Шилов Г.Е.). Математика и действительность // Историко-мате-матические исследования. Вып. 20 (1975).

Клайн М. Математика. Поиск истины. М., 1988.

Клайн М. Математика. Утрата определенности. М., 1984.

Колмогоров А. Н. Математика в ее историческом развитии / Под ред. В.А. Успен­ского. М., 1991.

Лакатос И. Доказательства и опровержения. Как доказывают теоремы. М., 1967.

Молодший В.Н. Очерки по философским вопросам математики. М., 1969.

Новиков СП. Вторая половина XX века и ее итог: кризис физико-математи­ческого сообщества в России и на Западе // Историко-математические исследо­вания. Вторая серия. М., 2002. Вып. 7 (42).

Образование, которое мы можем потерять: Сборник / Под общ. ред. В.А. Садов-ничего. М., 2002.

Перминов В.Я. Философия и основания математики. М., 2001.

Степин B. C. Теоретическое знание. М., 2003.

Стили в математике: социокультурная философия математики / Под ред. А. Г. Ба-рабашева. СПб., 1999.

Целищев В.В. Философия математики. Новосибирск, 2002. Ч. I.

Яновская С.А. Из истории аксиоматики // Историко-математические иссле­дования. М., 1958. Вып. 11.

Kitcher Ph. The Nature of Mathematical Knowledge. N.Y., 1983.

Wilder R. Mathematics as a Cultural System. Oxford, 1981.