Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

 Расчет надкрановой части. Этот расчет, выполняемый в плоскости и из плоскости поперечной рамы, производится аналогично расчету сплошных колонн.

Расчет подкрановой части. Расчет выполняется в плоскости и из плоскости поперечной рамы.

РАСЧЕТ В ПЛОСКОСТИ РАМЫ.

Особенностями расчета являются следующие:

1) расчет выполняется по I и II группам предельных состояний;

2) расчет продольной арматуры производится на действие наиболее неблагоприятных (опасных) сочетаний усилий в сечениях 3-3 и 4-4 с M_max, M_min, Q_max:

1. M_max, N_соот, Q_соот;

2. M_min, N_соот, Q_соот;

3. M_соот, N_соот, Q_max.

Сочетание усилий с Q_max используется при расчете ветвей и при расчете средних распорок. Опасным может также оказаться сочетание с небольшой продольной силой N и значительным изгибающимся моментом М, так как в этом случае одна из ветвей может испытывать растяжение – см. ниже формулу (26.3). Продольные силы в ветвях колонны определяются по формулам:

       N_b1,2 = 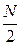±  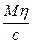                                                           (26.1)

или

 

           

 

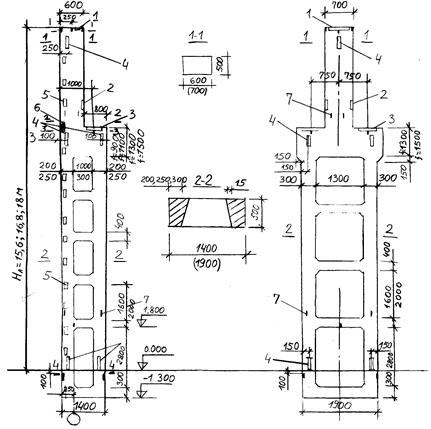
Рис.26.1 Двухветвевые колонны крайнего (а) и среднего (б) ряда

 

N_b1 = 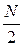+  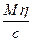;                                                      (26.2)

 

        N_b2 = 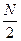 –  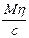,                                                       (26.3)

где с – расстояние между осями подкрановых ветвей (рис.26.2);

ŋ = 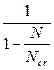      – коэффициент продольного изгиба

При N_b >0 ветвь сжата, при N_b<0 – растянута.

В зависимости от величин М и N возможны два случая напряженного состояния ветвей:

Случай 1. Обе ветви сжаты (N_b1 >0, N_b2 >0). В этом случае поперечная сила передается поровну на каждую ветвь, а момент в ветви равен (рис.26.2, б)

   М_br = 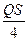,                                                          (26.4)

где Q – величина поперечной силы при рассмотренном сочетании усилий;

S = 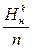    – средний шаг распорок;

n – число проемов.

Расчет арматуры каждой ветви производится методом итераций по формулам внецентренного сжатия для случая симметричного армирования на усилия N_b1, М_br и N_b2, М_br. Изначально принято, что каждая ветвь армирована симметрично, но не обязательно одинаково с другой ветвью (т.к. усилия в ветвях различны).

Случай 2. Одна ветвь сжата (N_b1>0), а другая – растянутая (N_b2<0) (рис.26.2, в). В этом случае из-за возможности образования нормальных трещин считается, что растянутая ветвь имеет пониженную жесткость, вследствие чего вся поперечная сила передается на сжатую ветвь, момент в которой равен:

М_br = 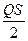,                                                       (26.5)

Арматура сжатой ветви A_s = A  определяется по формулам внецентренного сжатия, а арматура растянутой ветви A_s = A  – по формуле центрального растяжения:

A_s = A´_s =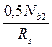

После выполненных расчетов на все опасные сочетания усилий назначается окончательное армирование на стадии эксплуатации из расчета в плоскости поперечной рамы. Оно принимается одинаковым в обеих ветвях (рис.26.3, а) средней колонны, что обусловлено попеременным действием в различных направлениях равных по величине изгибающих моментов. Армирование ветвей крайней колонны может быть как одинаковым (при незначительной разности величин противоположно направленных моментов), так и различным (в случае их значительной разницы) (рис.26.3, б).

Расчет по образованию и раскрытию (в случае образования) нормальных трещин выполняется как в растянутых ветвях, так и во внецентренно сжатых. При а_crc > a_crc,ult производится увеличение арматуры A_s = A .

Расчет поперечной арматуры A_sw выполняется по аналогии с расчетом в колоннах сплошного сечения.

РАСЧЕТ ИЗ ПЛОСКОСТИ РАМЫ

Он производится по аналогии с расчетом колонн сплошного сечения на N_max . При выполнении условия

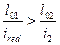                                                                                                (26.6)

этот расчет можно не выполнять.

В условии (26.6):

l_o1,l_o2 – расчетная длина подкрановой части в плоскости и из плоскости рамы, соответсвующая сочетанию N_max ;

i_red = 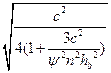     – приведенный радиус инерции в плоскости рамы;

ψ =  ;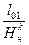

h_b – высота сечения ветви;

n – общее число проемов;

i₂= 0,289b – радиус инерции сечения при расчете из плоскости рамы.

 

 

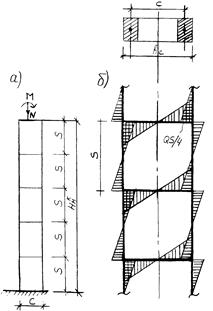
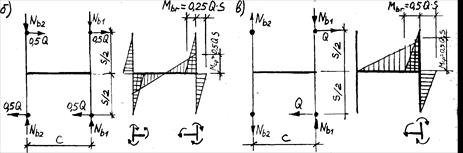
Рис.26.2 К расчету подкрановой части

а – расчетная схема; б – схема усилий и эпюра М от местного изгиба

при двух сжатых ветвях; в – то же, при одной растянутой ветви и другой сжатой.

а)                                                                       б)

 

 

Рис.26.3 Варианты армирования ветвей

а – одинаковое армирование; б – различное

РАСЧЕТ СРЕДНЕЙ РАСПОРКИ

Средняя распорка является изгибаемым элементом. Целью расчета является

определение требуемого количества продольной и поперечной арматуры.

При определении продольной арматуры различают 2 случая:

Случай 1. Обе ветви сжаты (N_b1>0; N_b2>0). В этом случае эпюра является знакопеременной (рис.26.4, а), и арматура распорки принимается симметричной:

A_s = A  = ,

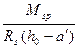где M_sp=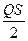  

Случай 2. Одна ветвь сжата (N_b1>0), а другая растянута (N_b2<0) (рис.26.4, б). В этом случае распорка армируется несимметричной арматурой A_s ≠ A . Растянутая арматура определяется по формуле :

A_s  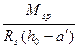=                                                          (26.7)

при M_sp=Q·S.

Сжатая арматура A  устанавливается по конструктивным требованиям.

Расчет поперечной арматуры выполняется на действие поперечной силы, равной:

Q_sp = ,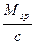

где M_sp= 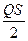    – в случае 1;

 M_sp=Q·S – в случае 2.

Далее производится расчет по образованию и раскрытию нормальных и наклонных трещин.

РАСЧЕТ ПОДКРАНОВОЙ РАСПОРКИ

Подкрановая распорка является одновременно изгибаемым и коротким сжатым элементом (l_пр/h₀ ≤0,9 ,где l_пр – вылет распорки, h₀ – рабочая высота распорки), из-за чего ее разрушение может произойти по нормальному сечению и по наклонной сжатой полосе

                

 

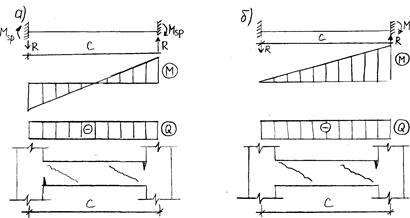
Рис.26.4 К расчету средней распорки (расчетная схема, эпюры М и Q, возможная схема разрушения)

а – в случае обеих сжатых ветвей; б – в случае одной ветви сжатой, а другой – растянутой

(рис.26.5, а).

В соответствии с этим целью расчета является определение требуемого количества продольной и поперечной арматуры. К поперечной арматуре относятся горизонтальные и вертикальные стержни сеток, которыми армируется распорка.

 Расчет выполняется на действие опасных сочетаний усилий в сечении 3–3.

 

                

 

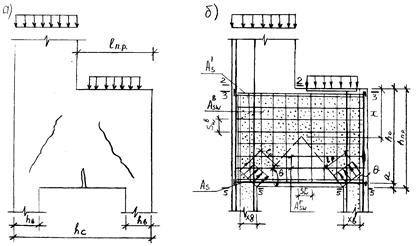
Рис.26.5 К расчету подкрановой распорки

а – возможные схемы разрушения; б – расчетная схема и схема армирования.

 

Нижняя продольная арматура A_s рассчитывается на действие изгиб момента, возникающего от силы N_max (т.о., в этом случае опасным является сочетание усилий M_соот, N_max, Q_соот в сечении 3–3). Ее определение производится методом итераций по формуле:

A_s =      ,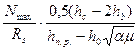

где h_c – высота сечения подкрановой части;

h_b – высота сечения ветви;

h_п.р – высота подкрановой распорки;_.

h₀ – рабочая высота подкрановой распорки;

α = E_s / E_b ;

μ = A_s / bh₀ – коэффициент армирования. В первом приближении принимают μ =0,001bh₀ с последующим уточнением A_s.

Поперечная арматура распорки рассчитывается на действие поперечной силы Q, действующей в сечении 3–3 по оси ветвей и равной наибольшему значению из следующих величин:

 

Q = max 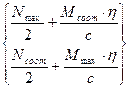                                                   (26.8)

 

 В этом случае распорка рассматривается как короткий сжатый элемент. Расчетным является сечение 5–5 в месте соединения ветви с распоркой. Если вся поперечная сила Q воспринимается сжатым бетоном сечения 5–5, то A_sw ставится конструктивно. Если нет, то A_sw устанавливается по расчету. При этом усилия в A 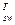 и А 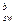 проектируются на плоскость длиной l_p (а затем на сечение 5–5), длина которой зависит от высоты сжатой зоны ветвей (l_p= x_b / sin 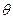), а наклон определяется углом 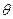, зависящим от величины х в самой распорке (рис.26.5).

 Верхняя продольная арматура A  рассчитывается на срез от силы Q по формуле (26.9) с учетом сопротивления срезу бетона, горизонтальных стержней сеток A 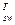 и нижней продольной арматуры A_s:

A = 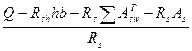,                                     (26.9)

где R_sh = 2R_bt – расчетное сопротивление бетона срезу;

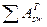– суммарная площадь поперечного сечения горизонтальных стержней сеток;

Q – по формуле (26.8)

Далее выполняется расчет по образованию и раскрытию нормальных и наклонных трещин.