1. Цель работы: ознакомление с устройством спектроскопа и основами спектрального анализа. Градуировка спектроскопа. Исследование спектров испускания водорода.
2. Краткая теория
Спектры, испускания. Излучение света различными телами при их нагревании до высоких температур принято называть тепловым, или температурным излучением.
Если свет от раскалённого тела пропустить через призму, то на экране за призмой получим непрерывную цветную полосу, которая носит название непрерывного, или сплошного спектра испускания. Такой спектр получается, например, от раскалённой вольфрамовой нити лампы накаливания.
Если источником света являются нагретые разреженные газы или излучение, полученное при электрическом разряде в разреженном газе, то картина спектра существенно меняется: вместо непрерывно переходящих одна в другую цветных полос наблюдаются несколько цветных ярких линий, разделённых тёмными промежутками. Такие спектры называются линейчатыми. Линейчатые спектры испускания возникают в тех случаях, когда источником излучения служат отдельные атомы или ионы химических элементов, находящихся в газообразном состоянии.
Если источником излучения служат не атомы или ионы, а отдельные молекулы веществ, то получается, так называемый, полосатый спектр. По виду, полосатый спектр похож на линейчатый, однако, в полосатом спектре наблюдаются широкие цветные полосы на тёмном фоне.
Спектры, образуемые излучением нагретых тел или при электрическом разряде в разреженном газе, называются спектрами испускания, или эмиссионными спектрами.
Спектры поглощения. Если белый свет пропустить сквозь прозрачную среду: твёрдую, жидкую или газообразную, то вследствие поглощения средой некоторых длин волн в спектре белого света будут затемнены соответствующие участки (полосы) или линии, характерные для этой среды.
Совокупность тёмных линий или полос, образующихся в сплошном спектре белого света при прохождении его сквозь данную среду, называется спектром поглощения или абсорбционным спектром.
Согласно закону Кирхгофа, атомы поглощают излучения тех же длин волн, которые они испускают в возбуждённом состоянии, поэтому тёмные линии поглощения наблюдаются в тех же местах, где лежали бы линии спектра испускания.
Спектральный анализ. Спектры испускания и поглощения тесно связаны со строением атомов и молекул вещества. Спектр вещества является одной из важнейших его характеристик. В природе не существует двух разных веществ с одинаковым спектром. Поэтому по характеру спектра можно судить о природе и составе как простых, так и сложных веществ. Метод качественного и количественного (по интенсивности линий) определения состава вещества по его спектру называется спектральным анализом.
Основным преимуществом спектрального анализа перед химическим является то, что он может быть сделан с весьма незначительным количеством веществ, значительно меньшим, чем это требуется для химического анализа. Путём спектрального анализа может быть обнаружено присутствие в веществе примеси в количестве до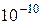 
г. Этим методом в своё время были открыты ряд редких элементов (рубидий, цезий и др.), встречающихся в природе в очень небольших количествах. Спектральный анализ позволил установить состав Солнца и других небесных тел.
Закономерности в атомных спектрах. Излучение невзаимодействующих друг с другом атомов состоит из отдельных спектральных линий, характерных для каждого химического элемента. Было замечено, что линии в атомных спектрах располагаются в строгом порядке, образуя группы или серии линий с определёнными длинами волн и интенсивностями. Отчетливее всего это обнаруживается в спектре простейшего атома — водорода.
В 1885г. преподаватель математики швейцарской высшей школы Бальмер вывел формулу, которая позволяла очень точно рассчитывать длины волн спектральных линий видимой области спектра водорода:
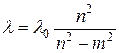, (1)
где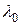 
— константа; n — целое число, принимающее значения 3, 4, 5 и т. д.; 
.
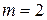Позднее в спектре испускания водорода были открыты и другие серии линий. В ультрафиолетовой области — серия Лаймана, в инфракрасной — серии Пашена, Брекета, Пфунда. В результате обобщения огромного экспериментального материала, а также теоретических исследований была выведена эмпирическая формула, описывающая все линии спектра водорода и называемая формулой Бальмера-Ридберга:
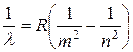, (2)
где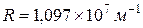 
— постоянная Ридберга. При этом серии Лаймана соответствует значение m =1, серии Больмера m=2, серии Пашена m=3 и т. д. При заданном 
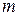число 
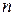принимает все целочисленные значения, начиная с m+1.
Величина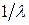 
называется волновым числом, под которым в спектроскопии понимают число длин волн, укладывающихся на единицу длины.
Объяснение природы линейчатых спектров. Закономерности, наблюдаемые в атомных спектрах, долгое время оставались непонятыми. Спектр водорода был впервые объяснен теоретически Н. Бором. В основу своей теории Нильс Бор положил ядерную модель атома Резерфорда. Он предположил, что электроны движутся вокруг ядра (протона) по круговым орбитам. Согласно законам классической электродинамики электрон должен излучать электромагнитные волны и поэтому продолжительное его пребывание на орбите невозможно. Постепенно теряя свою энергию, электрон должен упасть на ядро. Кроме того, по мере приближения к ядру частота излучения электрона должна была бы непрерывно изменяться. Следовательно, спектр излучения атома водорода должен быть непрерывным, а не линейчатым. Однако, опыты показывают, что атомы — устойчивые образования, и спектр атома — линейчатый. Отсюда вытекает вывод, что законы классической электродинамики неприменимы к внутриатомным процессам.
Бор перенёс на атом представление о квантах, выдвинув следующие три постулата:
1. Электроны в атоме могут двигаться не по любым орбитам, а только по орбитам вполне определённого радиуса. На этих орбитах, получивших название стационарных, или разрешённых, момент количества движения (импульса) электрона кратен величине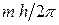 
, т. е.
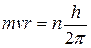, (3)
где m — масса электрона;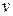 
— его линейная скорость; r — радиус орбиты; n —целое число (n=1, 2, 3, 4...), называемое квантовым числом (номер орбиты); h — постоянная Планка.
2. Движение электрона по стационарной орбите не сопровождается излучением или поглощением энергии.
3. При переходе электрона с одной стационарной орбиты на другую излучается или поглощается квант энергии. Частота излучаемого или поглощаемого излучения определяется из условия:
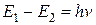, (4)
где E 1 и Е2 — значения энергии электрона до и после перехода;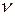 
— частота света, излучаемого или поглощаемого атомом.
Величина кванта энергии зависит от того, с какой орбиты на какую переходит электрон.
Таким образом, атом водорода существует в таких стационарных состояниях, которым соответствуют дискретные значения энергии:
, 
, 
, …. 
.
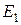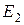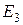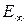Расположение энергетических уровней простейшего атома — атома водорода, показано на рис. 7.
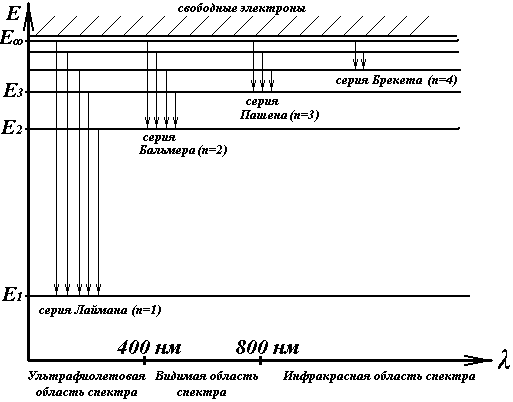
Рис. 7.
При движении по ближней к ядру орбите (n=1) электрон обладает минимальной энергией 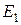. При переходе электрона на орбиту большего радиуса энергия его возрастает (уровни энергии 
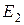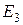, , и т. д.). Такой переход электрона может происходить только тогда, когда атом получает энергию извне. Перескоки электронов на отдалённые орбиты ведут к возбуждённому состоянию атома. Возбуждённое состояние атома является малоустойчивым. По истечении так называемого среднего времени жизни, которое составляет по порядку величины всего 
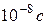, электрон вновь совершает обратный скачок в основное состояние (на орбиту, ближайшую к ядру), или же последовательно проходит следующие друг за другом низшие промежуточные состояния. Эти переходы, изображенные на рис. 1 стрелками, сопровождаются уменьшением энергии электрона. Выделившаяся при этом энергия испускается в пространство в виде монохроматического излучения с определённой частотой, определяемой формулой (4).
Значение энергии 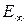и выше (заштрихованная область) соответствует уходу электрона на бесконечное расстояние от ядра. Практически это означает полное высвобождение электрона из атома, причём атом становится ионом.
Теория Бора была крупным шагом в развитии теории атома. Она с полной отчётливостью показала неприменимость классической физики к внутриатомным явлениям и главенствующее значение квантовых законов в микромире.
В настоящей работе исследуемый спектр получается с помощью одного из простейших спектральных приборов — призменного спектроскопа, в котором происходит пространственное разделение лучей с различными длинами волн благодаря дисперсии света.
Дисперсия света — явление, обусловленное зависимостью показателя преломления вещества от длины световой волны. Эту зависимость можно охарактеризовать функцией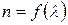 
.
Быстроту изменения показателя преломления с изменением длины волны, т. е. величину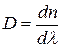 
, называют дисперсией вещества.
Для всех прозрачных веществ с уменьшением длины волны происходит монотонное возрастание показателя преломления, т. е. для фиолетовых лучей (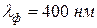 
) он будет больше, чем для красных ( 
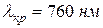). Такая дисперсия называется нормальной. На рис. 8 приведены опытные данные показателя преломления в зависимости от длины волны для стекла (кривая 1) и кварца (кривая 2).
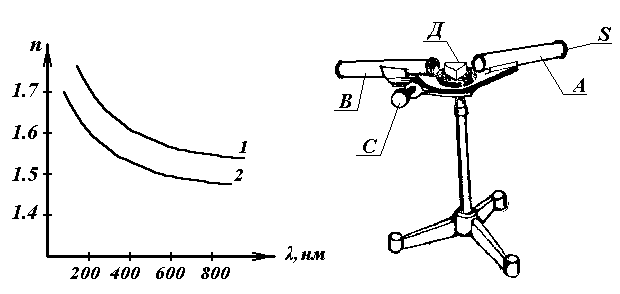
Рис. 8. Рис. 9.
Описание установки
Внешний вид и принципиальная схема спектроскопа приведены на рис. 9, и рис. 10. Спектроскоп состоит из треножного штатива (рис. 9), на котором укреплены следующие части: коллиматор А, зрительная труба В и столик с призмой Д. Коллиматор А состоит из оптической трубы, в которой окуляр заменён щелью S. Щель помещена в главном фокусе объектива O 1 (рис. 10), поэтому лучи, идущие из неё, выходят из объектива параллельным пучком. Ширину щели S можно менять с помощью винта.
Лучи из объектива О1 падают на переднюю грань призмы Д (рис. 10), в которой разлагаются и выходят параллельными пучками разных цветов и направлений, смотря по их составу. Пройдя призму, лучи поступают в оптическую трубу В через объектив О2, который даёт изображение спектра в фокальной плоскости линзы О3. Так как выходящие из призмы пучки параллельных лучей различных цветов имеют различное направление, то в фокальной плоскости линзы О3 получается ряд параллельных изображений этих пучков (ряд цветных линий), которые рассматриваются через окуляр О3 трубы В.
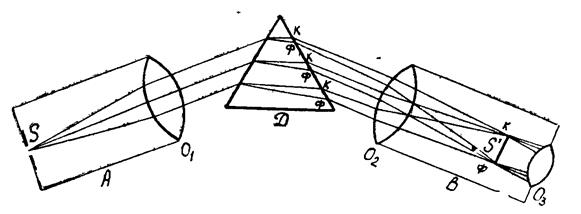
Рис. 10.
Для определения относительного положения линий спектра в окулярной трубе имеется указатель (чёрная визирная нить), который при помощи микрометрического винта С (рис. 9) можно передвигать и совмещать с любой спектральной линией. Отсчёт положения трубы производят по основной шкале и нониусу. Основная шкала — линейная — имеет миллиметровые деления. Барабан микровинта разделен на 50 частей. Ход микровинта равен 1 мм, следовательно, цена одного деления на барабане микровинта (нониуса)
.
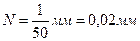Положение каждой спектральной линии можно характеризовать числом целых миллиметров (определяемых по линейной шкале) плюс число сотых миллиметра (определяемых по нониусу умножением числа делений нониуса на 0,02 мм).
Работа заключается в градуировке шкалы спектроскопа (задание № 1) и в исследовании линейчатого спектра испускания водорода, т. е. в определении длины волны линий, наблюдаемых в спектре этого газа (задание 2).
Градуирование спектроскопа имеет целью выразить показания прибора в длинах волн. Для этого пользуются спектральными трубками, наполненными специально очищенными газами, находящимися под давлением около 1 мм рт. ст. и имеющими в средней части капилляр, в котором при пропускании разряда происходит наиболее интенсивное свечение. В качестве источника тока взята индукционная катушка, питаемая постоянным током от выпрямителя.
Спектральная трубка укрепляется на штативе в вертикальном положении и присоединяется к клеммам вторичной обмотки индукционной катушки. Нельзя, чтобы трубка работала в то время, когда не производится наблюдение, так как от продолжительной работы она начинает светиться менее интенсивно.
Щель предварительно установленного спектроскопа следует возможно ближе придвинуть к капилляру спектральной трубки, причём она должна быть расположена параллельно капилляру, т. е. вертикально.
Градуирование спектроскопа можно вести по любой трубке, если известны длины волн находящегося в ней газа. Длины волн для градуирования, их расположение и цвет даны в табл. 3.
Порядок выполнения работы
Задание 1 . Градуирование спектроскопа
1. Подключить трубку с гелием или неоном к индукционной катушке и включить ток.
2. Наблюдая спектр газа и, осторожно вращая микровинт, привести указатель окуляра (визирную нить) оптической трубы спектроскопа в совпадение с первой, хорошо различимой линией, например, ярко-красной. Сделать отсчёт по основной шкале и нониусу спектроскопа. Затем, вращая микровинт, перевести указатель на следующую, хорошо видимую линию и опять сделать отсчёт по шкале спектроскопа и т. д. Результаты измерений занести в табл. 1, предварительно записав в неё известные длины волн спектра, по которому ведётся градуировка. Длины волн спектра выписать из табл. 3.
3. Построить градуировочный график, откладывая на миллиметровой бумаге по оси абсцисс длины волн, а по оси ординат — показания прибора.
Таблица 1
| Цвет спектральной линии в спектре гелия или неона | Длины волн для гелия или неона (ось Х) | Показания шкалы спектроскопа для линий гелия или неона (ось У) |
Задание2 . Исследование спектра испускания водорода и определение длин волн основных линий серии Бальмера
1. Подключить трубку с водородом к индукционной катушке и включить ток.
2. Совмещая визирную нить окуляра с различными линиями в спектре водорода, сделать отсчёт по шкале спектроскопа. Результаты отсчёта занести в табл. 2.
3. Пользуясь градуировочной кривой спектроскопа (задание 1), определить длины волн отдельных линий водорода. Для этого нанести на ось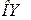 
показание по шкале спектроскопа и из этой точки восстановить перпендикуляр до пересечения с кривой градуирования. Опуская из точки пересечения перпендикуляр на ось 
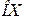, найти соответствующее значение длины волны в спектре водорода.
4. Найденные значения длин волн занести в табл. 2.
Таблица 2
| Цвет спектральной линии в спектре водорода | Показания шкалы спектроскопа | Длина волны | Погрешность | |
| из графика | из таблицы 3 | |||
5. Вычислить длины волн спектральных линий водорода, относящихся к серии Бальмера по формуле (1), используя значение константы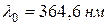 
.
6. Сопоставить длины волн, полученные с помощью графика, с длинами волн, вычисленными по формуле (1).
Контрольные вопросы
1. Какой спектр излучают раскалённые металлы?
2. Какая разница между сплошным, линейчатым и полосатым спектрами?
3. В чём заключается спектральный анализ? В чём его преимущество перед химическим анализом?
4. Какие опыты говорят о том, что законы классической электродинамики неприменимы к внутриатомным процессам?
5. Какое объяснение природы спектров даёт квантовая теория?
6. Какими электронными переходами в атоме водорода вызываются спектральные линии серий Лаймана, Бальмера и Пашена?
7. Что такое дисперсия света? Какая дисперсия называется нормальной?
8. С какой целью производится градуировка спектроскопа?
9. Как по градуировочной кривой спектроскопа произвести спектральный анализ?
Таблица 3 Значения длин волн основных спектральных линий гелия и неона
| Элемент | Характеристика спектральных линий | Длина волны в нм (1 нм=10-9м) |
|
Гелий
| Красная 1-я слабая | 706,5 |
| Красная 2-я яркая | 657,8 | |
| Желтая | 587,6 | |
| Зеленая 1-я | 501,6 | |
| Зеленая 2-я | 492,2 | |
| Голубая | 471,3 | |
| Синяя | 447,1 | |
| Фиолетовая I-я | 402,6 | |
| Фиолетовая II-я | 388,9 | |
|
Неон
| Красная яркая | 640,2 |
| Красно-оранжевая из двух близких линий, лежащих ближе к красному концу спектра | 614,3 | |
| Оранжевая, ближайшая к следующей линии № 4 | 594,5 | |
| Жёлтая яркая | 585,2 | |
| Светло-зелёная, ближайшая к линии № 4 | 576,0 | |
| Зелёная из двух одиноких линий, лежащих ближе к красному концу спектра | 540,0 | |
| Зелёная из двух одиноких линий, лежащая ближе к фиолетовому концу | 533,0 | |
| Зеленая правая из пяти равноудалённых линий | 503,1 | |
| Сине-зелёная одинокая | 484,9 |
ЛАБОРАТОРНАЯ РАБОТА № 14
Проверка закона Малюса
1. Цель работы: экспериментальная проверка закона Малюса.
Оборудование: поляроид, источник света, фотоэлемент, гальванометр.
Краткая теория
С помощью специальных поляризационных приспособлений (призма Николя, поляроид и т.д.) естественный свет может быть преобразован в линейно поляризованный. Основное свойство таких приспособлений заключается в том, что они могут пропускать световые волны, электрический вектор напряжённости которых колеблется лишь в строго определенных направлениях. Эго направление называется главным направлением.
В настоящей работе для получения и исследования линейно поляризованного света применяются поляроиды. Они изготовляются из очень мелких кристаллов турмалина или герапатита (сернокислого иод-хинина), нанесённых на целлулоидную плёнку. Оптические оси всех кристалликов специальным способом ориентированы в одном направлении. Кристаллы герапатита почти полностью поглощают обыкновенный луч. Таким образом, падающий естественный свет, проходящий сквозь поляроид, становится плоско поляризованным. Рассмотрим установку(рис.11).
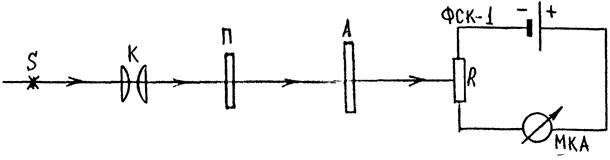
Рис. 11.
Здесь S — источник света, П — поляризатор, А — анализатор, R — сопротивление, ФСК-1 — фотоэлемент.
Пройдя сквозь первый поляроид П (поляризатор), свет становится поляризованным. Второй поляроид А (анализатор) может пропускать только те колебания, которые совпадают с его главным направлением. Если главные направления поляризатора и анализатора совпадают, то интенсивность проходящего света будет максимальной.
Если же анализатор повернуть таким образом, что его главное направление составляет угол 900 с главным направлением поляризатора, то интенсивность проходящего света будет равна 0.
Такое положение поляроидов называется скрещенным. В том случае, когда главное направление поляроидов составляет между собой некоторый угол φ, интенсивность проходящего света будет принимать промежуточные значения.
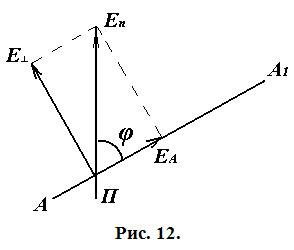Найдём зависимость между интенсивностью I и углом φ. Пусть 
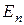— амплитуда вектора напряжённости, пропускаемого поляризатором, АА1 — главное направление анализатора. Амплитуду 
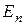можно разложить на две взаимно перпендикулярные составляющие 
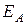и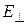 
, одна из которых совпадает с главным направлением анализатора (рис. 12).
Колебания, перпендикулярные направлению АА1 не проходят через анализатор.
Видно, что амплитуда выходящего из анализатора света равна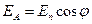 
. Так как интенсивность пропорциональна квадрату амплитуды, то:
, 
, 
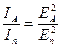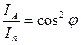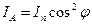— закон Малюса.
Здесь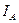 
— интенсивность света, прошедшего через анализатор, 
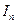— интенсивность света прошедшего через поляризатор. Если 
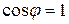, то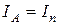 
.
Порядок выполнения работы
1. Вначале, вращая анализатор, добиваются максимального отброса стрелки гальванометра. При этом нужно следить за тем, чтобы стрелка прибора не зашкаливала. При необходимости увеличить или уменьшить интенсивность источника света.
2. Установить стрелку анализатора в положение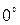 
и записать показания гальванометра.
3. Повернуть анализатор на 10° и вновь записать показания гальванометра. Произвести измерения от 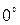до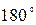 
, каждый раз записывая показания гальванометра.
4. Построить график зависимости силы фототока, пропорциональной интенсивности проходящего света, от квадрата косинуса угла поворота:
.
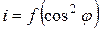Контрольные вопросы
1. Естественный и поляризованный свет. Плоскость колебаний, плоскость поляризации.
2. Способы получения поляризованного света.
3. Поляризаторы и анализаторы. Каков механизм поляризации света в поляроидах?
4. Устройство и принцип действия призмы Николя.
5. Поляроиды, их вид и механизм поляризации. Дихроизм.
ЛАБОРАТОРНАЯ РАБОТА № 15
Дата: 2018-12-21, просмотров: 630.
