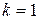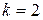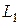ФИЗИКА
Лабораторный практикум
(Часть IV )
По разделу «Оптика»
для студентов 1 курса всех форм обучения
по направлениям подготовки бакалавров
100800.62 «Товароведение»
260800.62 «Технология продукции и организация общественного питания»
ОРЕЛ
Издательство ОрелГИЭТ
2012
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФГБОУ ВПО "Орловский государственный институт
экономики и торговли»
ФИЗИКА
Лабораторный практикум
(Часть IV )
По разделу «Оптика»
для студентов 1 курса всех форм обучения
по направлениям подготовки бакалавров
100800.62 «Товароведение»
260800.62 «Технология продукции и организация общественного питания»
ОРЕЛ
Издательство ОрелГИЭТ
2012
УДК 53
ББК 22.3
Ф 912
Подготовлено на кафедре математики и естествознания
Рекомендовано Методическим советом инженерно-технологического
факультета
Рецензент: кандидат технических наук, доцент Орловского государственного института экономики и торговли Глазова Г.В.
Фролов М.А., Ашихина Л.А. Физика. Лабораторный практикум по разделу «Оптика» для студентов 1 курса всех форм обучения по направлениям подготовки бакалавров: 100800.62 «Товароведение», 260800.62 «Технология продукции и организация общественного питания» (Часть IV). – Орёл: Издательство ОрелГИЭТ, 2012. - 35 с.,
Пособие содержит учебный материал по четвёртой части цикла лабораторных работ — оптике, атомной и ядерной физике. Приведены сведения по технике безопасности при выполнении лабораторных работ, контрольные вопросы для самопроверки по каждой лабораторной работе.
Материал данного пособия рекомендуется к использованию при изучении дисциплины «Физика» для студентов 1 курса всех форм обучения по направлениям подготовки бакалавриата.100800.62 «Товароведение» и 260800.62 «Технология продукции и организация общественного питания».
УДК 53
ББК 22.3
Ф 912
© М.А. Фролов, 2012
© Л.А. Ашихина, 2012
© Орел ГИЭТ , 2012
СОДЕРЖАНИЕ
ПРАВИЛА ТехникИ безопасности при выполнении лабораторных работ (ЧастЬ IV) 4
Рекомендации к подготовке и выполнению лабораторных работ (частЬ IV) 5
Лабораторная работа №12
Определение показателя преломления и концентрации сахара в водном растворе при помощи рефрактометра. 5
Лабораторная работа №13
Исследование линейчатых спектров испускания. 12
Лабораторная работа №14
Проверка закона Малюса. 20
Лабораторная работа №15
Определение показателя преломления стекла с помощью микроскопа. 22
Лабораторная работа №16
Определение предельного угла полного внутреннего отражения и показателя преломления стекла. 27
Лабораторная работа №17
Определение длины световой волны с помощью дифракционной решётки. 30
РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА.. 33
ПРАВИЛА ТехникИ безопасности при выполнении
Лабораторных работ (частЬ IV )
Во время домашней подготовки к лабораторным работам №12-17, в целях экономии времени на занятии, рекомендуется тщательно изучить порядок выполнения данных работ.
Для выполнения лабораторной работы №12, рекомендуется дома набрать в маленький пузырёк немного вина из бутылки, при этом необходимо записать содержание сахара, которое должно быть указано на этикетке бутылки. При выполнении работы в лаборатории, в качестве дополнительного задания, проверить концентрацию сахара в вине рефрактомтром и сопоставить результаты.
Для подготовки к работам №13 и №15, ознакомиться (повторить) п.3 лабораторной работы №1 (часть I), а именно, правила измерения штангенциркулем и микрометром.
Для расчётов по лабораторным работам 14 и 16 необходимо иметь инженерные калькуляторы.
ЛАБОРАТОРНАЯ РАБОТА № 12
Определение показателя преломления
и концентрации сахара в водном растворе
При помощи рефрактометра
1. Цель работы — изучение законов преломления света и оптических свойств вещества. Определение концентрации сахара в водном растворе при помощи рефрактометра
Краткая теория
Законы преломления света. Из опыта известно, что в однородной среде свет распространяется прямолинейно, однако если луч света попадёт на границу раздела двух различных прозрачных сред под некоторым углом, то он частично отражается, частично проходит в другую среду, причём несколько изменяет своё направление.
Изменение направления света при переходе из одной среды в другую называется преломлением или рефракцией. Доля отражённого на границе двух сред света тем больше, чем больше разница в показателях преломления этих сред и чем больше угол падения света.
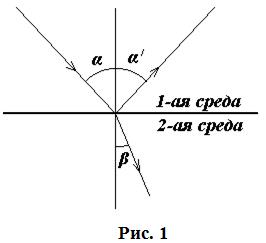
Опытным путём были установлены следующие законы преломления света (рис. 1):
1. Луч преломлённый, луч падающий и перпендикуляр, проведённый к границе раздела двух сред в точке падения, лежат в одной плоскости.
2. Отношение синуса угла падения (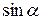 
) к синусу угла преломления ( 
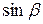) для данных двух сред есть величина постоянная, называемая показателем преломления второй среды относительно первой:
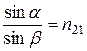(1) 
Относительный показатель преломления является величиной постоянной для данных сред, не зависит от угла падения и определяется только оптическими свойствами граничных сред.
Показатель преломления вещества по отношению к вакууму принято называть абсолютным показателем преломления данного вещества.
Обычно оптические свойства вещества характеризуются показателем преломления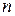 
относительно воздуха, который мало отличается от абсолютного показателя преломления ( 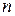вакуума=1, 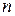воздуха =1,003). Среда, у которой абсолютный показатель преломления больше, называется оптически более плотной.
Показатель преломления зависит от длины волны света. Его обычно относят к монохроматическому жёлтому излучению паров натрия (длина волны 589 нм).
В табл. 1 приведены показатели преломления некоторых жидких и твёрдых веществ относительно воздуха.
Таблица 1
| Вещество |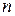
| Вещество |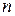
|
| Жидкости Вода Спирт этиловый Глицерин Масло: касторовое льняное подсолнечное | 1,33 1,36 1,47 1,48 1,47 1,47 | Твёрдые тела Лёд Слюда Янтарь Стекло (лёгкий крон) Стекло (тяжёлый флинт) Алмаз Канадский бальзам | 1,31 1,56—1,60 1,55 1,57 1,80 2,42 1,53 |
Объяснение закона преломления света с точки зрения волновой теории.
Закон преломления света может быть получен исходя из его волновой природы, если воспользоваться принципом Гюйгенса.
Согласно этому принципу каждую точку среды, до которой дошла световая волна, можно рассматривать как источник вторичных сферических волн, распространяющихся по всем направлениям со скоростью света в данной среде; новый фронт волны представляет собой сгибающую всех сферических вторичных волн в некоторый момент времени t.
Рассмотрим распро-странение световой волны с плоским волновым фронтом. На границу раздела двух сред MN с показателями преломления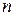 
1 и 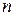2 падает плоский волновой фронт АВ (рис. 2). Ему соответствует пучок параллельных лучей, составляющих с нормалью АК угол i.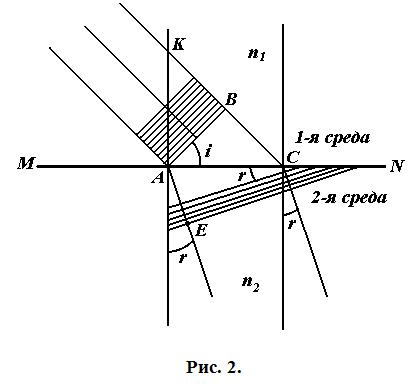 
В первой среде свет распространяется со скоростью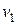 
, во второй — со скоростью 
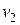, причём 
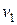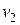> . Все точки, до которых доходит волновой фронт, становятся источниками новых сферических волн. Пусть за время 
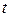элементарная волна из точки В, распространяясь в первой среде, пройдёт расстояние ВС= 
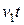. Элементарная волна, распространяясь во второй среде, пройдет расстояние AE= 
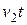. СЕ— новый фронт волны. В точках A и С построим падающий и преломлённый лучи и проведём перпендикуляр к поверхности раздела сред.
В ΔВАС угол при вершине А равен углу падения i, а в ΔАСЕ угол при вершине С равен углу преломления r (как углы, образованные взаимно перпендикулярными сторонами). Выражая синусы этих углов через стороны треугольников, получим для относительного показателя преломления n21 следующее выражение
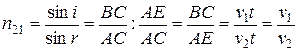. (2)
Таким образом, показатель преломления второй среды относительно первой равен отношению скорости света в первой среде к скорости света во второй среде.
В то же время относительный показатель преломления второй среды относительно первой n 21 равен отношению абсолютных показателей преломления второй и первой сред:
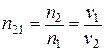. (3)
Абсолютные показатели преломления двух веществ обратно пропорциональны скоростям распространения в них света, то есть, в веществе оптически более плотном, свет распространяется медленнее, чем в веществе оптически менее плотном.
Используя соотношение (3), можно дать определение абсолютного показателя преломления вещества.
Отношение скорости распространения света в вакууме с к скорости распространения его в данной среде v называется абсолютным показателем преломления данного вещества.
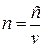. (4)
Предельное преломление и полное внутреннее отражение. При отражении и преломлении света отношение величин отраженной и преломленной световой энергии зависит от угла падения лучей и оптических свойств граничных сред.
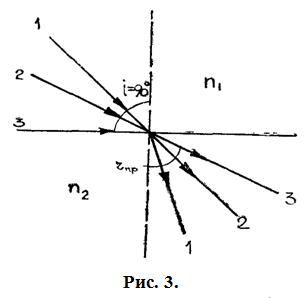При распространении света из среды оптически менее плотной в среду оптически более плотную (n 1 < n 2) величина отраженной световой энергии сильно возрастает с увеличением угла падения луча, а величина преломлённой световой энергии уменьшается. В этом случае угол преломления меньше угла падения (рис. 3). Следовательно, при увеличении угла падения (лучи 1 и 2) до i =90° (луч 3) свет во второй среде будет распространяться только в пределах угла r пр, называемого предельным углом преломления.
Величина предельного угла rпр определяется из условия
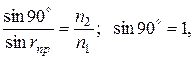
следовательно,
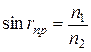. (5)
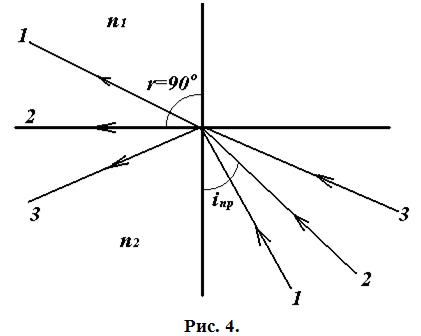
Если свет распространяется из среды оптически более плотной в среду оптически менее плотную (n 1 > n 2), то здесь доля отражённой световой энергии также возрастает с увеличением угла падения, однако, начиная с некоторого угла падения 
, вся световая энергия луча отражается от границы раздела, и свет не проходит из более плотной среды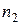 
в менее плотную среду 
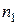. Это явление носит название полного внутреннего отражения (рис. 4). В этом случае угол преломления r больше угла падения i. Следовательно, свет преломляется (переходит в другую среду) в пределах угла падения 
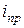, соответствующего углу преломления r =90° (луч 2).
Свет, падающий под большим углом, полностью отражается от границы сред (луч 3).
Угол 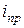называется предельным углом полного внутреннего отражения. Величина этого угла определяется из условия
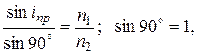
следовательно,
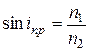. (6)
Нетрудно доказать, что вследствие обратимости хода лучей для двух данных сред предельный угол преломления равен предельному углу полного отражения.
Если среда с показателем преломления n 1 (рис. 4) является воздухом, для которого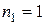 
, то формула (6) примет вид:
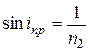. (7)
Предельные углы полного внутреннего отражения на границе с воздухом для некоторых веществ приведены в табл. 2.
Таблица 2
| Вещество | Предельный угол полного внутреннего отражения в град. |
| Вода | 49 |
| Стекло (легкий крон) | 40 |
| Стекло (тяжелый флинт) | 34 |
| Алмаз | 24 |
Полное внутреннее отражение используется при устройстве отражательных призм, применяемых в оптических приборах для поворота на 90° лучей, образующих изображение или для получения обратного (перевернутого) изображения. Во всех этих случаях лучи падают на соответствующую грань призмы под углом, большим предельного.
Полное внутреннее отражение используется также при устройстве гибких световодов, в которых свет, претерпевая многократное внутреннее отражение от стенок световода, может передаваться вдоль криволинейной траектории. В настоящее время этот принцип используется при устройстве приборов с волоконной оптикой. В них гибкий световод состоит из пучка тонких стеклянных нитей, каждая из которых покрыта оболочкой из вещества с меньшим показателем преломления. Такой световод может переносить свет от источника или, например, изображение предмета на значительные расстояния.
Явления предельного преломления и полного внутреннего отражения положены в основу конструкции прибора — рефрактометра, с помощью которого определяется показатель преломления вещества.
Описание установки
Величина показателя преломления некоторых растворов зависит от количества растворенного вещества, т. е. от концентрации вещества в растворе и температуры. Чем выше концентрация вещества в растворе (при одной и той же температуре), тем больше показатель преломления. Эта зависимость дает возможность определять концентрацию сахара в растворе по его показателю преломления.
В данной работе для определения показателя преломления n жидкости и определения концентрации сахара в ней применяется рефрактометр пищевой лабораторный РПЛ-3.
В основу конструкции прибора положен метод определения показателя преломления исследуемого раствора по предельному углу преломления или углу полного внутреннего отражения, Определение показателя преломления на приборе можно производить в проходящем и отраженном свете.
Внешний вид рефрактометра РПЛ-3 представлен на рис. 5. Он состоит из корпуса 1, колонки 2 и основания 3. К корпусу прибора крепятся камеры: верхняя 4 и нижняя 5. Нижняя камера с измерительной призмой жестко закреплена на корпусе, верхняя с осветительной призмой (откидная) шарниром 6 соединена с нижней камерой. В нижней и верхней камерах находятся окна. На нижней камере подвижно укреплен осветитель 7, свет которого можно направить в одно из окон камер.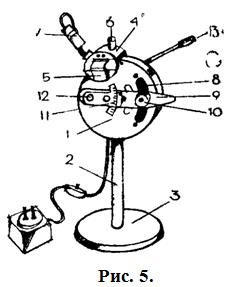 
На передней крышке прибора размещены шкала 8 и рукоятка 9 с окуляром 10, предназначенная для совмещения визирной линии сетки с границей светотени. На оси находится шкала 11 с винтом 12 для поворота дисперсионного компенсатора, помещённого внутри прибора с целью устранения спектральной окраски границы светотени. Винт 12 фиксирует шкалу в установленном положении. Для контроля температуры служит термометр 13, укреплённый на штуцере нижней камеры.
Основу прибора составляют две прямоугольные призмы из стекла с высоким показателем преломления 
, сложенные гипотенузными гранями, между которыми помещается тонкий слой (несколько капель) исследуемой жидкости (рис. 6).
На осветительную призму 3 от источника света направляется световой луч, который рассеивается, проходя тонкий слой исследуемого вещества, и преломляется на плоскости измерительной призмы 4. На границе двух сред, из которых одна должна быть оптически более плотной, чем другая, происходит явление предельного преломления или полного внутреннего отражения в зависимости от того, в преломленном или отраженном свете производится определение показателя преломления. Ход лучей в первом случае показан на рис. 6.
Рис. 6.
Свет, пройдя слой исследуемой жидкости, входит в измерительную призму по всевозможным направлениям, включая и угол падения, близкий к 90°. В измерительной призме лучи света проходят только в части её, соответствующей предельному углу преломления 
. Величина этого угла устанавливается с помощью зрительной трубы Т, объектив которой фокусирует параллельные лучи, выходящие из призмы в одинаковых направлениях. При установке трубы по направлению границы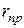 
часть поля зрения трубы будет светлой, часть — тёмной. По положению границы между ними можно установить величину угла 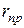, а по углу, согласно формуле (5), показатель преломления исследуемой жидкости
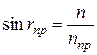или 
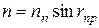, (8)
где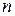 
— показатель преломления исследуемой жидкости, 
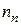— показатель преломления стекла призмы.
Порядок выполнения работы
В данной работе определяется показатель преломления жидкости и процентное содержание сахара в растворе.
1. Ознакомиться с конструкцией рефрактометра РПЛ-3.
2. Проверить установку нулевого отсчета шкалы прибора, для чего необходимо открыть верхнюю камеру, плоскости верхней и нижней камер промыть дистиллированной водой (можно спиртом) и досуха протереть чистой салфеткой. Затем, на плоскость измерительной призмы нанести две-три капли дистиллированной воды и закрыть верхнюю камеру. Рукоятку с окуляром опускают в нижнее положение и перемещают до тех пор, пока в поле зрения не появится граница светотени. Устранить окраску границы светотени поворотом винта дисперсионного компенсатора.
Затем поворачивают рукоятку окуляра, совмещая визирную линию сетки (три пунктирных штриха) с границей светотени, и производят отсчёт по шкале.
При правильной установке прибора на «нулевую» точку отсчета, граница светотени при 20°С должна быть совмещена с нулевым делением шкалы «0%», а также с делением n=1,33299 шкалы показателя преломления.
3. Произвести измерения с исследуемыми растворами.
Для проведения измерений открывают верхнюю камеру, досуха вытирают соприкасающиеся плоскости камер, на измерительную призму наносят две-три капли исследуемой жидкости и производят отсчёт после совмещения визирной линии с границей светотени.
Отсчёт нужно производить после закрытия камеры, через несколько минут для уравновешивания температурного режима.
Если измерения производятся при температуре, отличной от температуры 20°С, необходимо произвести пересчёт показаний на 20°С с учётом поправки на температуру по табл. 4.
4. Данные занести в табл. 3.
Таблица 3
| Номер раствора | Температура раствора, t°С | Показатель преломления n | %-ная концентрация сахара (по прибору) С | %-ная концентрация сахара с поправкой на температуру С t |
| 1 | ||||
| 2 | ||||
| 3 | ||||
| 4 | ||||
| 5 |
5. Построить график зависимости n от С t, откладывая по оси абсцисс С t, а по оси ординат соответствующие значения показателя преломления n.
Контрольные вопросы
1. Сформулируйте законы преломления света.
2. Каков физический смысл абсолютного и относительного показателя преломления?
3. Какую зависимость между показателями преломления и скоростями распространения света устанавливает волновая теория?
4. Объясните явления предельного преломления и полного внутреннего отражения.
5. Объясните принцип действия рефрактометра.
ЛаборатОРНАЯ РАБОТА № 13
Рис. 7.
При движении по ближней к ядру орбите (n=1) электрон обладает минимальной энергией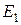 
. При переходе электрона на орбиту большего радиуса энергия его возрастает (уровни энергии 
, 
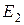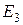, и т. д.). Такой переход электрона может происходить только тогда, когда атом получает энергию извне. Перескоки электронов на отдалённые орбиты ведут к возбуждённому состоянию атома. Возбуждённое состояние атома является малоустойчивым. По истечении так называемого среднего времени жизни, которое составляет по порядку величины всего 
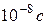, электрон вновь совершает обратный скачок в основное состояние (на орбиту, ближайшую к ядру), или же последовательно проходит следующие друг за другом низшие промежуточные состояния. Эти переходы, изображенные на рис. 1 стрелками, сопровождаются уменьшением энергии электрона. Выделившаяся при этом энергия испускается в пространство в виде монохроматического излучения с определённой частотой, определяемой формулой (4).
Значение энергии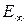 
и выше (заштрихованная область) соответствует уходу электрона на бесконечное расстояние от ядра. Практически это означает полное высвобождение электрона из атома, причём атом становится ионом.
Теория Бора была крупным шагом в развитии теории атома. Она с полной отчётливостью показала неприменимость классической физики к внутриатомным явлениям и главенствующее значение квантовых законов в микромире.
В настоящей работе исследуемый спектр получается с помощью одного из простейших спектральных приборов — призменного спектроскопа, в котором происходит пространственное разделение лучей с различными длинами волн благодаря дисперсии света.
Дисперсия света — явление, обусловленное зависимостью показателя преломления вещества от длины световой волны. Эту зависимость можно охарактеризовать функцией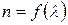 
.
Быстроту изменения показателя преломления с изменением длины волны, т. е. величину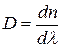 
, называют дисперсией вещества.
Для всех прозрачных веществ с уменьшением длины волны происходит монотонное возрастание показателя преломления, т. е. для фиолетовых лучей (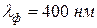 
) он будет больше, чем для красных ( 
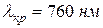). Такая дисперсия называется нормальной. На рис. 8 приведены опытные данные показателя преломления в зависимости от длины волны для стекла (кривая 1) и кварца (кривая 2).
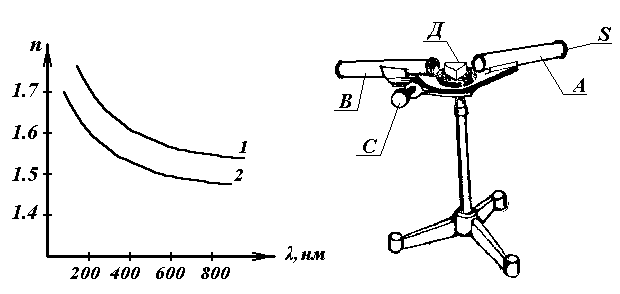
Рис. 8. Рис. 9.
Описание установки
Внешний вид и принципиальная схема спектроскопа приведены на рис. 9, и рис. 10. Спектроскоп состоит из треножного штатива (рис. 9), на котором укреплены следующие части: коллиматор А, зрительная труба В и столик с призмой Д. Коллиматор А состоит из оптической трубы, в которой окуляр заменён щелью S. Щель помещена в главном фокусе объектива O 1 (рис. 10), поэтому лучи, идущие из неё, выходят из объектива параллельным пучком. Ширину щели S можно менять с помощью винта.
Лучи из объектива О1 падают на переднюю грань призмы Д (рис. 10), в которой разлагаются и выходят параллельными пучками разных цветов и направлений, смотря по их составу. Пройдя призму, лучи поступают в оптическую трубу В через объектив О2, который даёт изображение спектра в фокальной плоскости линзы О3. Так как выходящие из призмы пучки параллельных лучей различных цветов имеют различное направление, то в фокальной плоскости линзы О3 получается ряд параллельных изображений этих пучков (ряд цветных линий), которые рассматриваются через окуляр О3 трубы В.
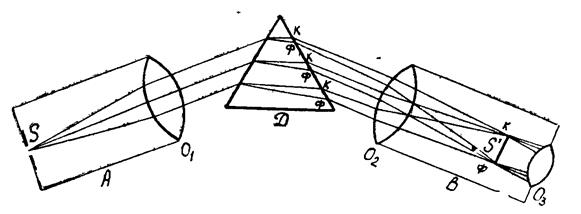
Рис. 10.
Для определения относительного положения линий спектра в окулярной трубе имеется указатель (чёрная визирная нить), который при помощи микрометрического винта С (рис. 9) можно передвигать и совмещать с любой спектральной линией. Отсчёт положения трубы производят по основной шкале и нониусу. Основная шкала — линейная — имеет миллиметровые деления. Барабан микровинта разделен на 50 частей. Ход микровинта равен 1 мм, следовательно, цена одного деления на барабане микровинта (нониуса)
.
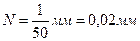Положение каждой спектральной линии можно характеризовать числом целых миллиметров (определяемых по линейной шкале) плюс число сотых миллиметра (определяемых по нониусу умножением числа делений нониуса на 0,02 мм).
Работа заключается в градуировке шкалы спектроскопа (задание № 1) и в исследовании линейчатого спектра испускания водорода, т. е. в определении длины волны линий, наблюдаемых в спектре этого газа (задание 2).
Градуирование спектроскопа имеет целью выразить показания прибора в длинах волн. Для этого пользуются спектральными трубками, наполненными специально очищенными газами, находящимися под давлением около 1 мм рт. ст. и имеющими в средней части капилляр, в котором при пропускании разряда происходит наиболее интенсивное свечение. В качестве источника тока взята индукционная катушка, питаемая постоянным током от выпрямителя.
Спектральная трубка укрепляется на штативе в вертикальном положении и присоединяется к клеммам вторичной обмотки индукционной катушки. Нельзя, чтобы трубка работала в то время, когда не производится наблюдение, так как от продолжительной работы она начинает светиться менее интенсивно.
Щель предварительно установленного спектроскопа следует возможно ближе придвинуть к капилляру спектральной трубки, причём она должна быть расположена параллельно капилляру, т. е. вертикально.
Градуирование спектроскопа можно вести по любой трубке, если известны длины волн находящегося в ней газа. Длины волн для градуирования, их расположение и цвет даны в табл. 3.
Порядок выполнения работы
Задание 1 . Градуирование спектроскопа
1. Подключить трубку с гелием или неоном к индукционной катушке и включить ток.
2. Наблюдая спектр газа и, осторожно вращая микровинт, привести указатель окуляра (визирную нить) оптической трубы спектроскопа в совпадение с первой, хорошо различимой линией, например, ярко-красной. Сделать отсчёт по основной шкале и нониусу спектроскопа. Затем, вращая микровинт, перевести указатель на следующую, хорошо видимую линию и опять сделать отсчёт по шкале спектроскопа и т. д. Результаты измерений занести в табл. 1, предварительно записав в неё известные длины волн спектра, по которому ведётся градуировка. Длины волн спектра выписать из табл. 3.
3. Построить градуировочный график, откладывая на миллиметровой бумаге по оси абсцисс длины волн, а по оси ординат — показания прибора.
Таблица 1
| Цвет спектральной линии в спектре гелия или неона | Длины волн для гелия или неона (ось Х) | Показания шкалы спектроскопа для линий гелия или неона (ось У) |
Задание2 . Исследование спектра испускания водорода и определение длин волн основных линий серии Бальмера
1. Подключить трубку с водородом к индукционной катушке и включить ток.
2. Совмещая визирную нить окуляра с различными линиями в спектре водорода, сделать отсчёт по шкале спектроскопа. Результаты отсчёта занести в табл. 2.
3. Пользуясь градуировочной кривой спектроскопа (задание 1), определить длины волн отдельных линий водорода. Для этого нанести на ось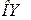 
показание по шкале спектроскопа и из этой точки восстановить перпендикуляр до пересечения с кривой градуирования. Опуская из точки пересечения перпендикуляр на ось 
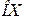, найти соответствующее значение длины волны в спектре водорода.
4. Найденные значения длин волн занести в табл. 2.
Таблица 2
| Цвет спектральной линии в спектре водорода | Показания шкалы спектроскопа | Длина волны | Погрешность | |
| из графика | из таблицы 3 | |||
5. Вычислить длины волн спектральных линий водорода, относящихся к серии Бальмера по формуле (1), используя значение константы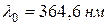 
.
6. Сопоставить длины волн, полученные с помощью графика, с длинами волн, вычисленными по формуле (1).
Контрольные вопросы
1. Какой спектр излучают раскалённые металлы?
2. Какая разница между сплошным, линейчатым и полосатым спектрами?
3. В чём заключается спектральный анализ? В чём его преимущество перед химическим анализом?
4. Какие опыты говорят о том, что законы классической электродинамики неприменимы к внутриатомным процессам?
5. Какое объяснение природы спектров даёт квантовая теория?
6. Какими электронными переходами в атоме водорода вызываются спектральные линии серий Лаймана, Бальмера и Пашена?
7. Что такое дисперсия света? Какая дисперсия называется нормальной?
8. С какой целью производится градуировка спектроскопа?
9. Как по градуировочной кривой спектроскопа произвести спектральный анализ?
Таблица 3 Значения длин волн основных спектральных линий гелия и неона
| Элемент | Характеристика спектральных линий | Длина волны в нм (1 нм=10-9м) |
|
Гелий
| Красная 1-я слабая | 706,5 |
| Красная 2-я яркая | 657,8 | |
| Желтая | 587,6 | |
| Зеленая 1-я | 501,6 | |
| Зеленая 2-я | 492,2 | |
| Голубая | 471,3 | |
| Синяя | 447,1 | |
| Фиолетовая I-я | 402,6 | |
| Фиолетовая II-я | 388,9 | |
|
Неон
| Красная яркая | 640,2 |
| Красно-оранжевая из двух близких линий, лежащих ближе к красному концу спектра | 614,3 | |
| Оранжевая, ближайшая к следующей линии № 4 | 594,5 | |
| Жёлтая яркая | 585,2 | |
| Светло-зелёная, ближайшая к линии № 4 | 576,0 | |
| Зелёная из двух одиноких линий, лежащих ближе к красному концу спектра | 540,0 | |
| Зелёная из двух одиноких линий, лежащая ближе к фиолетовому концу | 533,0 | |
| Зеленая правая из пяти равноудалённых линий | 503,1 | |
| Сине-зелёная одинокая | 484,9 |
ЛАБОРАТОРНАЯ РАБОТА № 14
Проверка закона Малюса
1. Цель работы: экспериментальная проверка закона Малюса.
Оборудование: поляроид, источник света, фотоэлемент, гальванометр.
Краткая теория
С помощью специальных поляризационных приспособлений (призма Николя, поляроид и т.д.) естественный свет может быть преобразован в линейно поляризованный. Основное свойство таких приспособлений заключается в том, что они могут пропускать световые волны, электрический вектор напряжённости которых колеблется лишь в строго определенных направлениях. Эго направление называется главным направлением.
В настоящей работе для получения и исследования линейно поляризованного света применяются поляроиды. Они изготовляются из очень мелких кристаллов турмалина или герапатита (сернокислого иод-хинина), нанесённых на целлулоидную плёнку. Оптические оси всех кристалликов специальным способом ориентированы в одном направлении. Кристаллы герапатита почти полностью поглощают обыкновенный луч. Таким образом, падающий естественный свет, проходящий сквозь поляроид, становится плоско поляризованным. Рассмотрим установку(рис.11).
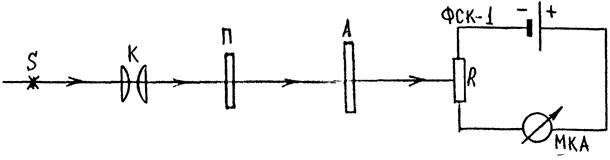
Рис. 11.
Здесь S — источник света, П — поляризатор, А — анализатор, R — сопротивление, ФСК-1 — фотоэлемент.
Пройдя сквозь первый поляроид П (поляризатор), свет становится поляризованным. Второй поляроид А (анализатор) может пропускать только те колебания, которые совпадают с его главным направлением. Если главные направления поляризатора и анализатора совпадают, то интенсивность проходящего света будет максимальной.
Если же анализатор повернуть таким образом, что его главное направление составляет угол 900 с главным направлением поляризатора, то интенсивность проходящего света будет равна 0.
Такое положение поляроидов называется скрещенным. В том случае, когда главное направление поляроидов составляет между собой некоторый угол φ, интенсивность проходящего света будет принимать промежуточные значения.
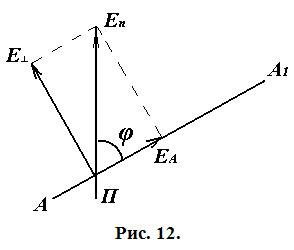Найдём зависимость между интенсивностью I и углом φ. Пусть 
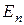— амплитуда вектора напряжённости, пропускаемого поляризатором, АА1 — главное направление анализатора. Амплитуду 
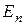можно разложить на две взаимно перпендикулярные составляющие 
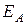и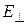 
, одна из которых совпадает с главным направлением анализатора (рис. 12).
Колебания, перпендикулярные направлению АА1 не проходят через анализатор.
Видно, что амплитуда выходящего из анализатора света равна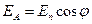 
. Так как интенсивность пропорциональна квадрату амплитуды, то:
, 
, 
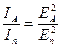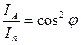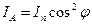— закон Малюса.
Здесь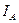 
— интенсивность света, прошедшего через анализатор, 
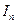— интенсивность света прошедшего через поляризатор. Если 
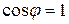, то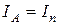 
.
Порядок выполнения работы
1. Вначале, вращая анализатор, добиваются максимального отброса стрелки гальванометра. При этом нужно следить за тем, чтобы стрелка прибора не зашкаливала. При необходимости увеличить или уменьшить интенсивность источника света.
2. Установить стрелку анализатора в положение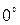 
и записать показания гальванометра.
3. Повернуть анализатор на 10° и вновь записать показания гальванометра. Произвести измерения от 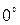до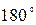 
, каждый раз записывая показания гальванометра.
4. Построить график зависимости силы фототока, пропорциональной интенсивности проходящего света, от квадрата косинуса угла поворота:
.
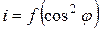Контрольные вопросы
1. Естественный и поляризованный свет. Плоскость колебаний, плоскость поляризации.
2. Способы получения поляризованного света.
3. Поляризаторы и анализаторы. Каков механизм поляризации света в поляроидах?
4. Устройство и принцип действия призмы Николя.
5. Поляроиды, их вид и механизм поляризации. Дихроизм.
ЛАБОРАТОРНАЯ РАБОТА № 15
С помощью микроскопа
1. Цель работы: определение показателя преломления стекла.
Оборудование: измерительный микроскоп с микрометрическим винтом; стеклянная пластинка с взаимно перпендикулярными штрихами на поверхностях; микрометр; осветитель для микроскопа.
Краткая теория
При прохождении света через плоскую границу двух прозрачных веществ неодинаковой оптической плотности падающий луч АО частично переходит во вторую среду (преломляется), а частично возвращается обратно (отражается). Направление преломлённого луча ОД и отражённого луча ОВ (рис. 13) определяется законами отражения и преломления света.
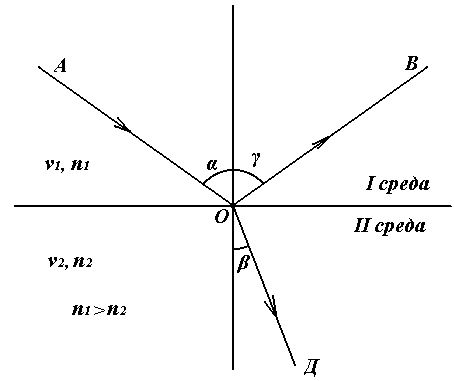
Рис. 13.
1. Луч падающий и отражённый лежат в одной плоскости с нормалью к границе раздела в точке падения (эта плоскость называется плоскостью падения), причём угол падения равен углу отражения:
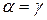. (1)
2. Преломлённый луч лежит в плоскости падения, причём отношение синусов угла падения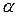 
и угла преломления 
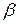для двух данных сред зависит только от длины световой волны, и не зависит от угла падения:
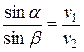. (2)
Здесь 
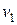и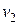 
— скорости распространения света в первой и второй средах.
Это отношение для двух данных сред обозначается:
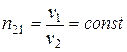, (3)
и называется показателем преломления второй среды относительно первой.
Закон преломления света может быть выведен из принципа Ферма или доказан построениями Гюйгенса. Показатель преломления данной среды относительно пустоты (вакуума) называется абсолютным показателем преломления среды. Абсолютные показатели преломления сред I и II равны:
,
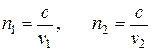где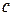 
— скорость распространения света в вакууме ( 
).
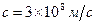Таким образом, для любой среды абсолютный показатель преломления есть отношение скоростей распространения света в пустоте и в данной среде:
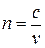. (4)
Показатель преломления зависит от длины волны света и от свойств среды. На опыте абсолютные показатели преломления всегда больше единицы, т. е. скорость распространения света в любой среде меньше, чем в пустоте.
Относительный показатель преломления двух сред связан с абсолютными показателям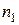и 
и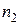 
соотношением:
.
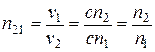Таким образом, закон преломления света может быть записан в виде:
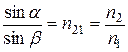. (5)
График на рис. 13 соответствует такому ходу лучей, когда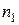 
> 
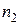, т.е. вторая среда является оптически более плотной и поэтому:
.
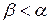Для определения показателя преломления веществ существуют различные методы. В данной работе используется кажущееся уменьшение толщины стеклянной пластинки вследствие преломления световых лучей проходящих через стекло, при рассматривании пластинки нормально к её поверхности. Схема прохождения лучей дана на рис. 14.
В точку А, находящуюся на нижней поверхности стеклянной пластины, падают два луча света 1 и 2. Луч 2 падает нормально к поверхности пластинки, проходит сквозь пластинку, не изменяя своего направления, и выходит в воздух в точке C.
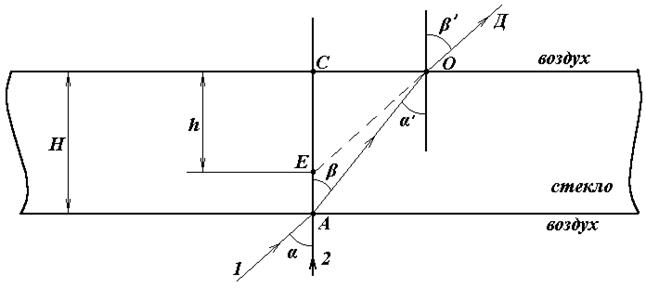
Рис. 14.
Луч 1, преломляясь, выходит из пластинки в точку О, в направлении Д. При выходе из пластинки луч ОД образует угол преломления β' больший, чем угол падения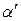 
. Если смотреть из точки Д по направлению ДО, то наблюдатель будет видеть пересечение лучей ОД и АС не в точке А, а в точке Е, т.е. кажущаяся толщина пластинки СЕ=h будет меньше её истинной толщины СА=Н. Для лучей, близких к нормально падающим, углы падения и преломления малы и синусы углов можно заменить их тангенсами. Рассматривая обратный ход лучей (от Д к А ), по закону преломления света напишем:
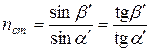. (6)
Из рисунка, после соответствующих преобразований, имеем:
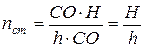. (7)
Следовательно, показатель преломления стекла в данном случае есть отношение истинной толщины стеклянной пластинки к её кажущейся толщине. Истинная толщина пластинки измеряется микрометром, а кажущаяся — микроскопом с микрометрическим винтом.
Микроскоп состоит из двух частей: механической и оптической. Механическая часть состоит из штатива, предметного столика (на нём устанавливают измеряемый или рассматриваемый объект) и тубуса, в котором смонтированы объектив и окуляр, составляющие оптическую часть. Из них окуляр обращён к глазу, а объектив к объекту наблюдения.
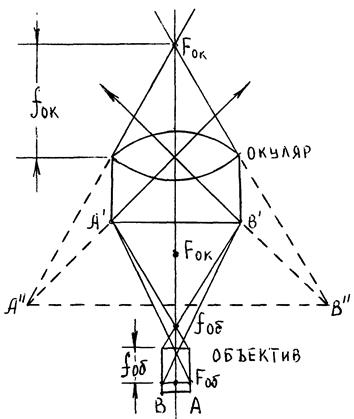
Рис. 15.
Объектив представляет собой систему линз, собранную в единой оправе. Он даёт увеличенное, действительное и обратное изображение предмета (А' В'), если предмет (АВ) помещён между f об и 2 f об (f об — фокусное расстояние объектива) рис. 15.
Окуляр представляет сложную лупу, обычно из двух линз, заключённых в короткую цилиндрическую трубку, вставляемую в верхнее отверстие тубуса. Окуляр, как и любая лупа, даёт увеличенное, мнимое, прямое изображение предмета (А"В"), которым в данном случае является изображение, даваемое объективом.
Следовательно, расстояние между объективом и окуляром должно выбираться так, чтобы изображение предмета, даваемое объективом, находилось от окуляра на расстоянии меньшем, чем его фокусное расстояние. Объективы обычно делают короткофокусными, а окуляры — длиннофокусными.
Наводка на резкое изображение в микроскопе осуществляется с помощью микрометрического винта.
Порядок выполнения работы
I. Измеряют микрометром истинную толщину стеклянной пластинки Н в том месте, где нанесены штрихи, результаты трёх измерений заносят в таблицу 1.
Таблица 1.
| № опыта
| Н, мм
| Отсчёт микрометрического винта
| h, мм
| |
| N | M | |||
| 1 | ||||
| 2 | ||||
| 3 | ||||
| Среднее значение | ||||
2. Определяют кажущуюся толщину стеклянной пластинки h, для чего пластинку кладут на столик микроскопа под объектив так, чтобы оба штриха пересекли оптическую ось прибора. Один из штрихов нанесён на верхнюю поверхность пластинки, а другой — на нижнюю. Поэтому в окуляре микроскопа одновременно нельзя увидеть чёткое изображение обоих штрихов. Сначала, двигая тубус, добиваются чёткого изображения штриха, нанесённого на верхнюю поверхность пластинки. Записывают отсчёт микрометрического винта, микроскопа, считая его затем за нулевое деление, т.е. от этого деления производят дальнейшие отсчёты. После этого опускают тубус микроскопа до получения чёткого изображения штриха на нижней поверхности пластинки, и тогда новый отчёт микрометрического винта сразу даёт кажущуюся толщину пластинки h, а именно:
,
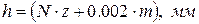где N — число полных оборотов барабана винта;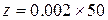 
— шаг винта, 50 — число делений в одном полном обороте барабана винта (за один полный оборот барабана микрометрического винта, тубус микроскопа перемещается на z=0.1 мм.); m — число делений в неполном обороте барабана. Отсчет N и m производят три раза.
3. Вычисляют показатель преломления стекла по формуле (7) из средних значений Н и h.
Контрольные вопросы
1. Что называется углом падения и углом преломления луча?
2. Сформулируйте законы отражения и преломления света.
3. Что называется абсолютным показателем преломления среды?
4. Как связаны между собой абсолютные и относительные показатели преломления двух сред?
5. От чего зависит показатель преломления среды?
6. Начертите и объясните ход лучей в плоскопараллельной пластине.
7. Начертите ход отражённого луча и преломлённого луча для n 1 > n 2 и n 1 < n 2.
8. Назовите основные части микроскопа.
9. Нарисуйте и объясните ход лучей в микроскопе.
10. Сформулируйте принципы Ферма и Гюйгенса.
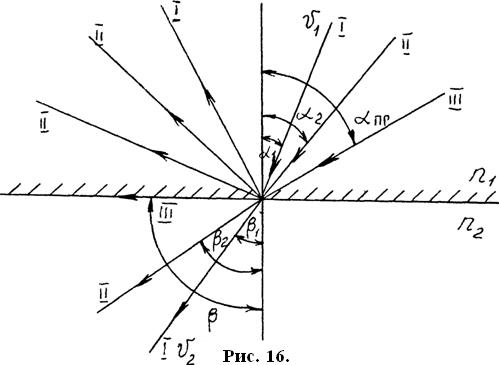
ЛАБОРАТОРНАЯ РАБОТА № 16
Краткая теория
Падая на границу раздела двух сред, луч света частично переходит из первой среды во вторую и при этом преломляется, а частично отражается от границы раздела и остаётся в первой среде.
Лучи падающий, отражённый, преломлённый и нормаль к границе раздела, восстановленная из точки падения, лежат в одной плоскости. Углы отсчитываются от нормали.
Энергия отражённого луча при увеличении угла падения увеличивается, а преломлённого соответственно уменьшается.
Скорость распространения света в вакууме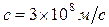 
, в любой другой среде, она всегда меньше 
.
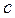Чем меньше скорость распространения света в данной среде, тем она оптически более плотная и имеет больший показатель преломления.
При переходе луча из среды менее плотной в среду более плотную угол падения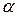 
больше угла преломления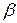 
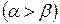, а при переходе луча из среды более плотной в среду менее плотную 
.
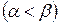Если увеличивать угол падения 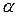луча, идущего из более плотной в менее плотную среду, то при некотором его значении угол преломления достигнет 
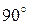и луч, не переходя по вторую среду будет скользить по границе раздела.
При дальнейшем увеличении угла падения луч будет полностью отражаться. Такое явление называется полным внутренним отражением (рис. 16). Угол падения, при котором угол преломления равен 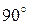, называется предельным углом полного внутреннего отражения.
Математически это явление легко описать с помощью законов преломления.
Если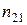 
— показатель преломления второй среды, относительно перво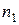й, 
и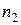 
— абсолютные показатели преломления этих сред (т.е. по отношению к вакууму), то
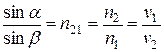. (1)
Обозначим через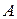 
предельный угол полного внутреннего отражения. Как уже сказано, если 
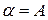, то 
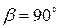и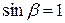 
, поэтому формула (1) переходит в формулу 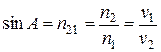(2):
. (2)
Из формулы (1) видно, что если взять угол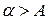 
, то, поскольку 
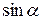должен быть больше 
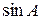, при данном значении 
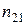придём к невыполнимому условию: 
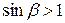. Это и значит, что преломлённого луча существовать не должно.
Порядок выполнения работы
1. Установить осветитель в верхнее положение (рис.17). Включить тумблер выпрямителя и проверить, проходит ли луч через центр полуцилиндрической линзы. В этом случае луч света проходит не преломляясь, так как он падает перпендикулярно к границе раздела.
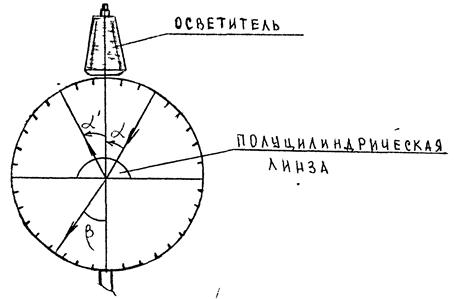
Рис. 17.
2. Отклонить осветитель по часовой стрелке на угол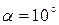 
, измерить соответствующий угол преломления 
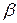. Увеличивать угол падения луча 
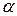до тех пор, пока угол преломления 
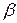не достигнет значения 
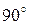. В этом случае преломлённый луч будет скользить по границе раздела, а угол 
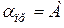будет предельным углом полного внутреннего отражения. Данные записать в таблицу 1.
Таблица 1.
|
| 
| 
| 
| 
| 
| 
| 
| 
|
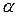
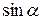
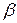
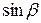
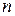
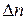
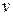
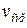
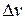
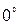
| 0 | |||||||
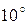
| 0.1736 | |||||||
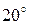
| 0.3420 | |||||||
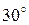
| 0.5000 | |||||||
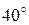
| 0.6428 | |||||||
| … |
3. Рассчитать по формуле (1) показатель преломления стекла, из которого сделана линза.
4. Вычислить абсолютную и относительную погрешность показателя преломления.
5. Определить по формуле (2) предельный угол полного внутреннего отражения и сравнить его значение с А, полученным экспериментально.
6. Определить скорость распространения луча 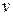в полуцилиндрической линзе по формуле (1). Вычислить 
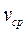и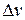 
.
Контрольные вопросы
1. Сформулируйте законы преломления.
2. При каких условиях возникает полное внутреннее отражение?
3. Какое явление называется полным внутренним отражением?
4. Напишите формулу для предельного угла полного внутреннего отражения.
5. Изобразите ход лучей при полном внутреннем отражении.
ЛАБОРАТОРНАЯ РАБОТА № 17
Краткая теория
Явление дифракции света состоит в нарушении законов геометрической оптики при распространении световых волн вблизи резких краёв прозрачных или непрозрачных тел, в том числе при прохождении через узкие отверстия. Это явление непосредственно следует из, принципа Гюйгенса-Френеля и с его помощью может быть полностью описано. Если речь идёт об одном отверстии, то получаемое позади него распределение освещённости не имеет резкой границы света и тени. Оно оказывается размытым и содержит ряд максимумов и минимумов, возникших вследствие интерференции вторичных когерентных волн от разных точек отверстия. Если же речь идёт о многих отверстиях, то распределение освещённости будет несколько иным, чем от одного отверстия, поскольку в нём дополнительно присутствует интерференционная картина, созданная волнами, прошедшими через разные отверстия.
В случае дифракционной решётки отверстия представляют собой параллельные друг другу прямолинейные узкие щели, причём каждая щель расположена на одинаковых расстояниях от соседних с нею щелей. Обычный способ изготовления такой решётки состоит в том, что на прозрачной плоскопараллельной пластинке специальным резцом процарапывают ряд параллельных штрихов. Эти штрихи непрозрачны и отделяют друг от друга неповреждённые участки пластинки, которые и служат щелями. Решётки невысокого качества можно изготовить фотографированием высококачественной решетки, нанесенной резцом. Схематически прозрачная решётка представлена на рис. 18. Здесь же показано прохождение через неё параллельного пучка света, то есть, плоского волнового фронта, при нормальном падении на поверхность решётки.
Рассмотрим распространение вторичных волн одинаковых точек двух соседних щелей. Если свет отклонился от своего первоначального направления на угол φ в результате дифракции, то при встрече двух вторичных волн в точке А (например в результате прохождения через собирающую линзу) окажется, что одна из них прошла путь больший, чем другая, на величину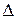 
.
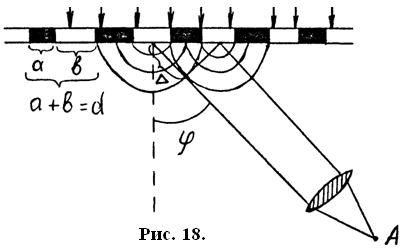
По рисунку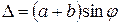 
. Здесь 
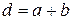— постоянная решётки, т.е. расстояние двух одинаковых точек соседних щелей: она равна сумме ширин штриха ( 
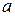) и щели ( 
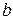).Если будет выполнено условие:
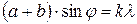, (1)
где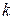 
— целое число 
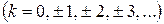, то в точке 
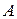волны усиливают друг друга, и мы будем наблюдать максимум. Число 
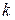, показывающее, сколько раз длина волны 
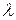укладывается в разности хода волн, называется порядком максимума.
Если падающий на решётку свет имеет сложный состав, то есть содержит различные длины волн, то после прохождения решётки он будет разложен на составные части — мы увидим спектр. Действительно, условие (1) при разных значениях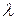 
требует и разных значений 
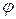, следовательно максимумы для разных длин волн будут наблюдаться под разными углами. Поскольку для данной 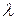условие (1) может выполняться при разных значениях 
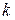, то максимум для каждой длины волны будет повторяться несколько раз, и спектров тоже будет несколько. Их называют спектрами 1-го, 2-го, 3-го и т.д. порядков. Число 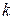может быть как положительным так и отрицательным, а это означает, что одинаковые спектры появятся как справа, так и слева от первоначального направления распространения. При 
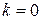, условие (1) выполняется для всех 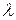, то есть, свет, прошедший без отклонения, не разлагается в спектр. Наибольшее число спектров определяется тем, что 
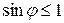, значит:
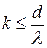. (2)
Из сказанного следует, что дифракционная решётка является спектральным прибором, т.е. служит для разложения сложного света в спектр и для измерения длин волн его составляющих. Последнее легко сделать, зная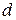 
и измеряя на опыте 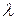. В данной работе это выполняется по упрощённой схеме, представленной на рис. 19.
Рейку на штативе устанавливают так, чтобы свет от источника через прорезь попадал на дифракционную решётку и затем в глаз наблюдателя. Если прорезь правильно освещена, то справа и слева от неё появится ряд повторяющихся спектров 1-го, 2-го и т.д. порядков, хорошо заметных на тёмном фоне миллиметровой шкалы.
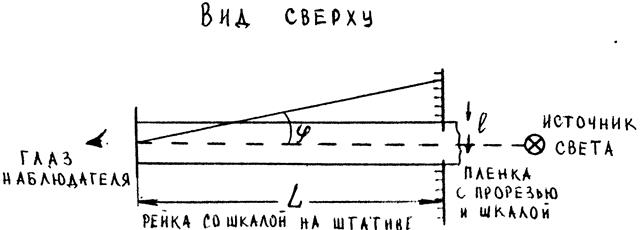
Рис. 19.
Эти спектры легко измерить по длине с помощь миллиметровой шкалы на планке. Если некоторой длине волны 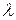в спектре 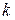-го порядка соответствует отсчёт 
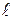,то при большом расстоянии 
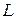между решёткой и планкой синус угла почти равен его тангенсу. Из рис. 19 видно, что 
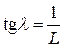, а значит и 
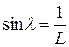. Подставляя это выражение в (1) получим:
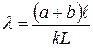. (3)
Для нашей решётки величина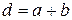 
составляет 0,01 мм и по измерениям 
и в спектре -го порядка длина волны 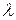определяется сразу. В данном случае требуется измерить крайние видимые длины волн на фиолетовом и красном краях спектра лампы накаливания или дневного света, т.е. определить коротковолновую и длинноволновую границы видимой области.
3. Порядок выполнения работы
1. Установить рейку горизонтально на уровне глаза, и приблизив глаз к дифракционной решётке, направить рейку на источник света так, чтобы были хорошо видны нейтральная прорезь вертикальной планки в конце рейки и шкала на ней. При этом справа и слева от прорези появятся отчётливо видимые спектры на тёмном фоне.
2. Установить планку на расстоянии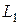 
от решётки (расстояние задаётся преподавателем) и по шкале на планке отсчитать начало и конец спектра для первых двух спектров слева и справа от прорези.
3. Установить планку на другом расстоянии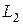 
(оно тоже задаётся преподавателем), повторить аналогичные измерения и занести их в таблицу.
4. По формуле (3) вычислить фиолетовую границу отдельно для 1-го и 2-го порядков, отдельно пр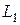и 
и 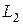, то есть, получить четыре значения 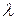, а затем из них найти среднее значение и абсолютную погрешность. Проделать аналогичные измерения для красной границы видимой области.
5. Все данные занести в таблицу.
Таблица
| Граница видимого спектра
|
|
|
| ||||
|
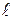вправо
|
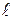влево
| 
|
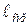
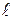вправо
|
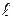влево
| 
| ||
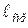
| Фиолетовая |
| ||||||
| красная | |||||||
| Фиолетовая |
| ||||||
| красная | |||||||
Контрольные вопросы
1. В чём состоит явление дифракции света?
2. Для чего служит дифракционная решётка?
3. Что такое постоянная дифракционной решётки?
4. Что такое порядок дифракционного максимума и порядок спектра?
5. Каков максимальный порядок спектра в дифракционной решетке?
6. Напишите основную формулу дифракционной решётки.
7. Чем отличается спектр, даваемый дифракционной решеткой, от спектра, даваемого призмой?
Рекомендуемая литература
1. Геворкян Р.Г., Шепель В.В. Курс физики. 1959
2. Зисман Г.А., Тодес О.М. Курс общей физики, т. 1. – М.: Наука, 1974. 337 с.
3. Рымкевич А.П. Сборник задач по физике. – М.: Просвещение, 1994. 224 с.
4. Савельев И.В. Курс общей физики, т 1. – М. : Наука, 1987.
5. Трофимова Г.И. Курс физики. Учебник для ВУЗов. М. : Высшая школа, 1989.
6. Шубин А.С. Курс общей физики. – М.: Высшая школа, 1976. – 480 с.
Фролов Марат Александрович
Ашихина Людмила Анатольевна
ФИЗИКА
Лабораторный практикум
(Часть IV )
По разделу «Оптика»
для студентов 1 курса всех форм обучения
по направлениям подготовки бакалавров
100800.62 «Товароведение»
260800.62 «Технология продукции и организация общественного питания»
Внутривузовское учебное издание
Литературный редактор Зайцева Н.Н.
Технический редактор Смагина И.В.
Подписано в печать . Формат 60х90/16.
Бумага книжно-журнальная. Гарнитура Times New Roman.
Усл.п.л.2.0 п.л. Тираж 50 экз. Заказ .
Издательство ОрелГИЭТ
302028, г. Орел, ул. Октябрьская, 12
Отпечатано с готового оригинал-макета на
полиграфической базе ОрелГИЭТ
ФИЗИКА
Лабораторный практикум
(Часть IV )
По разделу «Оптика»
для студентов 1 курса всех форм обучения
по направлениям подготовки бакалавров
100800.62 «Товароведение»
260800.62 «Технология продукции и организация общественного питания»
ОРЕЛ
Издательство ОрелГИЭТ
2012
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФГБОУ ВПО "Орловский государственный институт
экономики и торговли»
ФИЗИКА
Лабораторный практикум
(Часть IV )
По разделу «Оптика»
для студентов 1 курса всех форм обучения
по направлениям подготовки бакалавров
100800.62 «Товароведение»
260800.62 «Технология продукции и организация общественного питания»
ОРЕЛ
Издательство ОрелГИЭТ
2012
УДК 53
ББК 22.3
Ф 912
Подготовлено на кафедре математики и естествознания
Рекомендовано Методическим советом инженерно-технологического
факультета
Рецензент: кандидат технических наук, доцент Орловского государственного института экономики и торговли Глазова Г.В.
Фролов М.А., Ашихина Л.А. Физика. Лабораторный практикум по разделу «Оптика» для студентов 1 курса всех форм обучения по направлениям подготовки бакалавров: 100800.62 «Товароведение», 260800.62 «Технология продукции и организация общественного питания» (Часть IV). – Орёл: Издательство ОрелГИЭТ, 2012. - 35 с.,
Пособие содержит учебный материал по четвёртой части цикла лабораторных работ — оптике, атомной и ядерной физике. Приведены сведения по технике безопасности при выполнении лабораторных работ, контрольные вопросы для самопроверки по каждой лабораторной работе.
Материал данного пособия рекомендуется к использованию при изучении дисциплины «Физика» для студентов 1 курса всех форм обучения по направлениям подготовки бакалавриата.100800.62 «Товароведение» и 260800.62 «Технология продукции и организация общественного питания».
УДК 53
ББК 22.3
Ф 912
© М.А. Фролов, 2012
© Л.А. Ашихина, 2012
© Орел ГИЭТ , 2012
СОДЕРЖАНИЕ
ПРАВИЛА ТехникИ безопасности при выполнении лабораторных работ (ЧастЬ IV) 4
Рекомендации к подготовке и выполнению лабораторных работ (частЬ IV) 5
Лабораторная работа №12
Определение показателя преломления и концентрации сахара в водном растворе при помощи рефрактометра. 5
Лабораторная работа №13
Исследование линейчатых спектров испускания. 12
Лабораторная работа №14
Проверка закона Малюса. 20
Лабораторная работа №15
Определение показателя преломления стекла с помощью микроскопа. 22
Лабораторная работа №16
Определение предельного угла полного внутреннего отражения и показателя преломления стекла. 27
Лабораторная работа №17
Определение длины световой волны с помощью дифракционной решётки. 30
РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА.. 33
ПРАВИЛА ТехникИ безопасности при выполнении
Дата: 2018-12-21, просмотров: 836.
