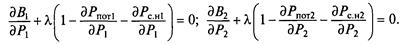При распределении нагрузки в энергосистеме надо учитывать расход мощности на собственные нужды и потери в ЛЭП. Если станция располагается далеко от потребителей, то экономия топлива в энергосистеме от ее использования может быть перекрыта дополнительным расходом топлива на компенсацию потерь.
Потери мощности в ЛЭП и расход мощности на собственные нужды электростанций учитываются в балансе мощностей энергосистемы, поэтому меняется балансовое уравнение ограничения. Оно получается путем нахождения условного экстремума при помощи метода неопределенных множителей Лагранжа, с учетом обновленного уравнения ограничения.
|
|
Целевая функция и уравнения связи те же, а балансовое уравнение ограничения будет включать в себя составляющие потерь мощности в ЛЭП и на собственные нужды электростанции:
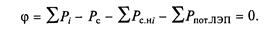
Вспомогательная функция Лагранжа
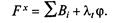
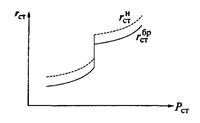
Рис. 13.18. Относительный прирост расхода топлива электростанции без учета потерь мощности на собственные нужды (брутто) и с учетом потерь (нетто)
|
|
| Учитывая, что |
| и обозначив |
Минимум функции Лагранжа совпадает с минимумом целевой функции, для нахождения которого частные производные по независимым переменным (нагрузкам отдельных станций) приравниваются нулю. Решая систему уравнений, можно получить условие оптимального распределения нагрузки между электростанциями в энергосистеме с учетом расхода мощности на собственные нужды и потерь в ЛЭП:
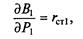
Численные значения относительных приростов, учитывающих потери мощности, составляют: σ = 0,05...0,06; σ = 0,1...0,15.
Учитывая, что значения а, р невысоки и меньше единицы, можно с небольшой погрешностью (0,5... 1,2%) заменить соотношение
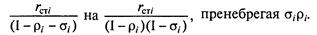
Тогда

т.е. влияние собственных нужд и потерь можно рассматривать независимо. Обозначив

где σ— относительный прирост расхода мощности на собственные нужды, который характеризует изменение расхода мощности на собственные нужды при изменении нагрузки на 1 МВт;
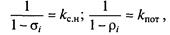
можно получить условия оптимального распределения нагрузки в энергосистеме:
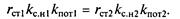
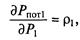
где p1 — относительный прирост расхода мощности на компенсацию потерь при изменении нагрузки на 1 МВт, можно получить следующие формулы:
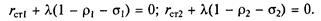
Тогда
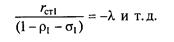
Таким образом,
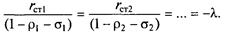
Относительный прирост расхода топлива электростанции без учета потерь мощности на собственные нужды и в сетях принято называть приростом брутто r бр ст , а с учетом потерь — нетто (r н ст). Таким образом (рис. 13.18):
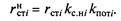
Тогда условие оптимального распределения нагрузок имеет следующий вид:
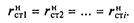
Дата: 2018-12-21, просмотров: 402.