Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

 

     Резкое увеличение скорости химической реакции с ростом температуры объясняет теория активации, согласно которой при столкновениях в химическую реакцию вступают только активные молекулы, обладающие по сравнению с другими некоторой избыточной энергией, называемой энергией активаци Е_а, кДж/моль.

     Энергия активации – это энергия, которую необходимо собщить 1 моль вещества, чтобы все молекулы в нем стали активными.

     Активация молекул возможна при нагревании или растворении вещества, при выделении энергии в ходе самой реакции, при поглощении ими квантов излучения (светового, радиоактивного, рентгеновского, и т.п.), под действием ультразвука или электрического разряда и даже при их ударах о стенку сосуда.

     С точки зрения теории активации исходные вещества сначала образуют неустойчивый активированный комплекс (АК). На это затрачивается Е_а прямой реакции, на величину которой возрастает энергия системы

                 AB + CD ↔ ‍AC + BD

С

А

С

А

А       С

                    

			+								+

D

DddddddDDDDDDDВDDD

В

D

В

В        D

                    

активированный комплекс

 

Далее происходит распад АК с образованием продуктов реакции и выделением энергии, которая численно равна энергии активации продуктов реакции.

    Если при распаде АК энергии выделяется больше, чем было затрачено на активацию исходных веществ (Е_а(прод)>E_a(исх)) то реакция экзотермическая, а если меньше (Е_а(прод)<E_a(исх)) – эндотермическая реакция.

Энергия образования активированного комплекса называется энергией активации Е_а. Реакция начинается только тогда, когда столкнувшиеся частицы будут обладать необходимой энергией активации и сумеют преодолеть энергетический барьер, ограничивающий их химическую активность.

    Разность энергий активации прямой и обратной реакции равна изменению энтальпии. Константа скорости реакции зависит от числового значения Е_а: чем меньше энергия активации, тем больше значение константы скорости реакции.

Возможность образования активированного комплекса, а соответственно и химического взаимодействия, определяется энергией молекул. Молекула, энергия которой достаточна для образования активированного комплекса, называется активной. Доля их в системе зависит от температуры.

Согласно уравнению Максвелла-Больцмана доля частиц с большей энергией (N_Ea), чем Ea, по отношению к общему числу молекул (N) составляет:

 

 

 

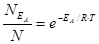
Рис. 1. Распределение молекул по энергиям при двух температурах (Т₂ > T₁).

Как видно на рис.1. с увеличением температуры растет доля молекул, энергия которых равна или выше энергии активации Е_а, соответственно растёт доля молекул способных к активным столкновениям с образованием активированного комплекса, т.е. происходит ускорение реакции. Чем выше энергия активации, тем меньше доля частиц, способных к активному взаимодействию. Экзотермические реакции протекают с меньшей энергией активации, чем эндотермические. Высокая энергия активации, или как иногда говорят, высокий энергетический барьер является причиной того, что многие химические реакции при невысоких температурах не протекают, хотя и принципиально возможны (ΔG < 0). В обычных условиях самопроизвольно не загораются: дерево, ткани, бумага, уголь, хлеб, керосин хотя ΔG < 0.

    При высоких температурах доля активных частиц достаточно велика и реакции идут быстро. При температурах 10000К и выше реакции завершаются за 10^-5-10^-3с. Раздел химии, изучающий реакции в низкотемпературной плазме, получил название плазмохимия. Плазмохимические реакции используются для очистки сточных вод, получения тугоплавких элементов и т.д.

Экспериментально установлено, что зависимость 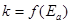достаточно точно передается уравнением Аррениуса.

,

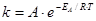где А – предэкспоненциальный множитель, отражающий долю эффективных соударений в общем числе соударений и не зависящий от температуры и концентрации;

R – универсальная газовая постоянная, Дж/мольК

Т – абсолютная температура, К

Е_а – энергия активации, Дж/моль

Запишем уравнение Аррениуса в диференциальном виде:

                               

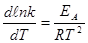
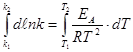
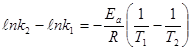
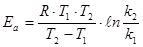
    Скорость химической реакции очень чувствительна к изменению температуры. Так как процесс образования активированного комплекса – эндотермический, то k реакции увеличиваеется с повышением температуры. Зависимость скорости гомогенной химической реакции от температуры описывается эмпирическим уравнением Вант-Гоффа:

 

,

 

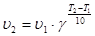где υ₁ и υ₂ – скорости реакции при температуре Т₁ и Т₂ соответственно;

γ – температурный коэфициент Вант-Гоффа, для большинства реакций лежит в интервале от 2 до 4.

Указанная математическая зависимость может быть выражена в виде правила: при повышении температуры на каждые 10 градусов скорость реакции возрастает в 2-4 раза, если реакция проводится при температуре, близкой к комнатной.

 

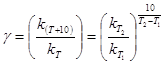
Есть определенная зависимость между скоростью реакции и временем.

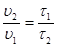     отсюда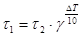   

 

Для ускорения очень медленно протекающих химических реакций применяют катализаторы – вещества, способные понижать энергию активации реакции, ослабляя связи между молекулами. При этом молекулы становятся реакционно-способными при более низких температурах. Изменение скорости реакции путем добавления небольших порций катализатора называют катализом. Увеличение скорости реакции в присутствии катализатора можно оценить по уравнению

,

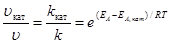где u_кат, k_кат – скорость и константа скорости реакции в присутствии катализатора; u, k –скорость и константа скорости реакции без катализатора; Е_{А, кат}, Е_А – энергия активации реакции в присутствии катализатора и без него.

 

Пример 1.  При 150 °С реакция заканчивается за 16 минут. Определите время, необходимое для протекания реакции при 200 °С, если температурный коэффициент Вант-Гоффа равен 2,5.

Р е ш е н и е

Между скоростью протекания химической реакции и ее продолжитель-ностью существует обратно пропорциональная зависимость

,

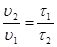тогда правило Вант-Гоффа в данном случае можно записать в виде

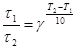, откуда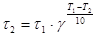 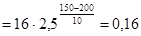мин.

 

Пример 2. Вычислите энергию активации реакции, если при повышении температуры от 290 К до 300 К скорость реакции увеличивается в 2 раза.

 

Р е ш е н и е

Согласно основному закону химической кинетики, скорость реакции и константа скорости реакции прямо пропорциональны друг другу, то есть выполняется соотношение

.

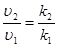
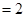Подставим это в формулу для расчета энергии активации

Е_А = 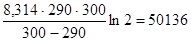Дж/моль.

Пример 3. Определите, на какую величину произошло снижение энергии активации при введении в систему катализатора, если при температуре 450 К в присутствии катализатора скорость реакции увеличилась в 1000 раз.

Р е ш е н и е

Преобразуем уравнение 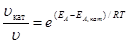 к виду

(Е_{А, кат} – Е_А) = R × T×ln .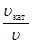

По условию задачи 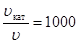, тогда

(Е_{А, кат} – Е_А) = 8,314 × 450 × ln1000 = 25844 Дж/моль.

 

§4. Химическое равновесие.

 

Все самопроизвольные реакции можно разделить на две группы:

1) необратимые реакции, идущие до конца и не изменяющие своего направления при изменении температуры и давления.

Химические реакции принято считать необратимыми, если: - один из продуктов выводится из зоны реакции в виде газа, осадка, малодисоциированного соединения или комплекса; -выделяется большое количество теплоты (реакция горения).

2) большинство химических реакций является обратимыми. При одних условиях они идут в прямом направлении, при других – в обратном, а при некоторых промежуточных – протекают одновременно в двух взаимно противоположных направлениях.

Любая химическая реакция может стать необратимой, если вывести вещество из зоны реакции или изменить условия её протекания. 

Состояние системы, при котором скорости прямой и обратной реакции равны, называются химическим равновесием, а концентрации реагирующих веществ равновесными.

По мере прохождения реакции наступит такой момент, когда .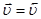

Такое состояние называется химическим равновесием.

H₂ + I₂ = 2HI

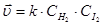
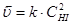
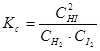
    Химическое равновесие является динамическим, т.е. его установление не означает прекращения реакции. Различают 2 вида химического равновесия: истинное и метастабильное (заторможенное).

 Признаки истинного химического равновесия: - скорости прямой и обратной реакций равны; - при сохранении внешних условий состояния системы не изменяется во времени; - при изменении внешних условий система приходит к новому состоянию равновесия; - состояние системы не зависит от того, с какой стороны она подходит к равновесию; - ΔG_P,T = 0 термодинамическое условие химического равновесия; - К_Р = 1.

    В общем случае для любой обратимой гомогенной реакции выражение константы равновесия может быть записано:

аА + вВ ↔ сС + дД

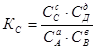
К_с – определяет глубину протекания процесса, если К_с → ∞, реакция является практически необратимой; если К_с → 0, то это свидетельствует о полном отсутствии взаимодействия между исходными веществами. В выражение для константы равновесия входят только равновесные концентрации газообразных участников реакции.

Химическое равновесие между газообразными веществами при небольших давлениях можно выразить с помощью парциальных давлений Р_i участников реакции:

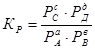
Между К_с и К_р существует определенное соотношение уравнение Менделеева-Клапейрона (Р ·V = C ·R ·T).

 

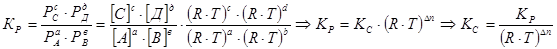
где Δn – разность числа мольгазообразных продуктов и исходных реагентов химической реакции.

Если реагенты находятся в состояниях отличных от стандартного, то изменение энергии Гиббса рассчитывается по уравнению изотермы Вант-Гоффа:

aA + bB = cC + dD

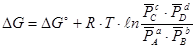
где 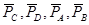 - относительное парциальное давление соответствующих веществ.

        

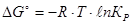
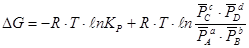
Для гетерогенных реакций закон действующих масс выполняется при условии, что в уравнения констант равновесия не входят равновесные концентрации (парциальные давления) твердых исходных веществ и продуктов реакции. Например, для гетерогенной реакции

С_графит + 2Н₂О_газ « СО₂ + 2Н₂

константа равновесия выражается уравнением

.

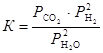Константа химического равновесия зависит от природы реагирующих веществ и от температуры. Влияние температуры на К определяется знаком теплового эффекта реакции. Для эндотермической реакции (Q < 0) при повышении температуры константа равновесия увеличивается, и наоборот, для экзотермической реакции (Q > 0) при возрастании температуры К уменьшается. Строгую связь между температурой и константой равновесия реакции, протекающей при постоянном давлении, отражает уравнение изобары Вант-Гоффа

,

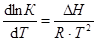где lnК – натуральный логарифм константы равновесия; DН – изменение энтальпии реакции; R – универсальная газовая постоянная; Т –абсолютная температура, К. Из уравнения видно, что при увеличении абсолютного значения энтальпии реакции и уменьшении температуры чувствительность К к изменению температуры повышается. Используя уравнение изобары Вант-Гоффа, можно вывести формулу для расчета среднего значения DН реакции, если известны значения константы равновесия при двух температурах

,

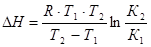где К₁, К₂ – константы равновесия реакции при температурах Т₁ и Т₂ соответственно.