Будем рассматривать обратимые процессы идеального газа. Среди них можно выделить так называемые политропные процессы, т.е. те, которые происходят при постоянной теплоемкости.
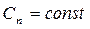 ,
, 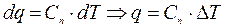
Уравнение состояния политропных процессов
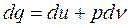 ;
; 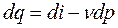
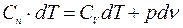 ;
; 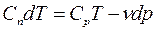
 ;
; 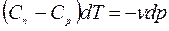
Второе уравнение разделим на первое.
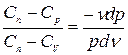 ;
; 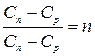
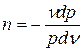 ;
; 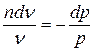 ;
; 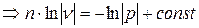
 (5.1)
(5.1)
(5.1) - уравнение политропных процессов
где n - показатель политропы, 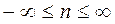
Выразим Сn: 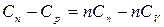 ;
; 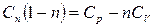 ;
;
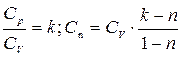 (5.2)
(5.2)
Формула (5.2) выражает теплоемкость политропного процесса. Рассмотрим формулы (5.1) и (5.2) при некоторых различных n:
1. 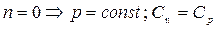 - процесс изобарный
- процесс изобарный
2. 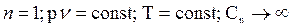 - процесс изотермический
- процесс изотермический
3.  - процесс адиабатный
- процесс адиабатный
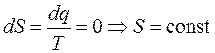 - процесс изоэнтропический
- процесс изоэнтропический
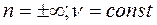
4. 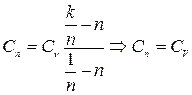 - процесс изохорный
- процесс изохорный
Так как 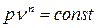 можно представить в виде
можно представить в виде 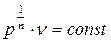
Связь между параметрами в политропных процессах
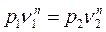 ;
; 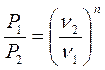 - закон Бойля-Мариотта (5.3)
- закон Бойля-Мариотта (5.3)
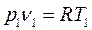 ;
; 
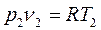 ;
; 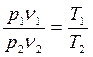
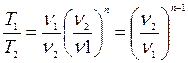 (5.4)
(5.4)
 (5.5)
(5.5)
Формула для работы:
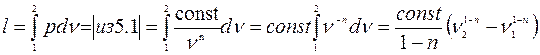 ;
;
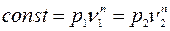
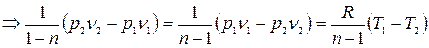
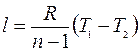
Формула (5.6) справедлива для бесконечного множества процессов, кроме изотермического.
Изотермический процесс:
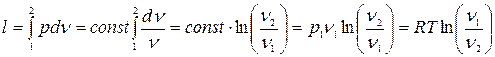
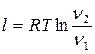 (5.7)
(5.7)
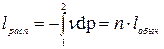
Изменение внутренней энергии:
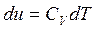 ;
; 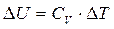 (5.8)
(5.8)
Формула (5.8) годна для всех процессов
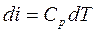 ;
;  (5.9)
(5.9)
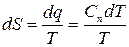 ;
; 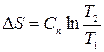
 (5.10)
(5.10)
Формула (5.10) справедлива для всех процессов, кроме изотермического. Для изотермического же процесса можно воспользоваться формулой (4.16).
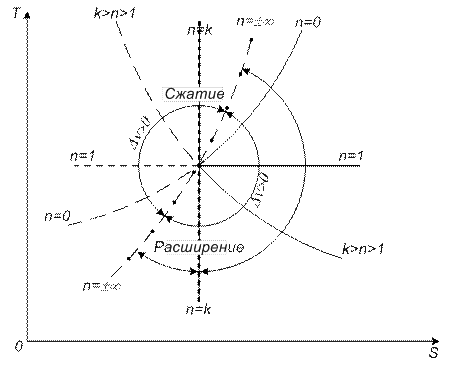
4.5 Pv – диаграмма политропных процессов
Изобарные процессы сжатия и расширения 
Изохорные процессы 
Рассмотрим изохорный процесс с ростом давления. Для него очевидно: 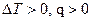 . Если тепло подводится к рабочему телу, то оно положительное, и если отводится, то отрицательное.
. Если тепло подводится к рабочему телу, то оно положительное, и если отводится, то отрицательное.
Методом от противного можно доказать, что во всех процессах правее и выше изотермического газ нагревается.
Аналогично можно показать, что для всех процессов правее адиабаты, теплота должна подводиться к газу.
Для процессов между изотермой и адиабатой 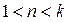 , Сn будет отрицательной (следует как из графика, так и из формулы (5.2)
, Сn будет отрицательной (следует как из графика, так и из формулы (5.2)

Ts – диаграмма политропных процессов
Второй закон термодинамики
Второй закон термодинамики, как и первый, - обобщение большого количества опытных данных.
Основные формулировки второго закона термодинамики:
1. Формулировка Клаузиуса: теплота самопроизвольно передается только от более нагретого тела к менее нагретому.
2. Формулировка Томпсона (Кельвина): невозможно создать циклически работающую тепловую машину, которая превращала бы в работу все подводимое тепло.
3. Формулировка Планка: вечный двигатель второго рода невозможен!
Раздел 5. Термодинамические циклы
Круговые процессы (циклы)
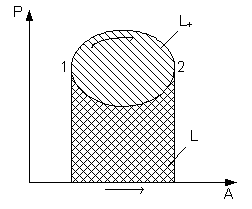 Совокупность термодинамических процессов, в результате которых система возвращается в исходное состояние, называется круговым процессом или циклом.
Совокупность термодинамических процессов, в результате которых система возвращается в исходное состояние, называется круговым процессом или циклом.
Цикл, в котором работа расширения больше работы сжатия, т.е. за счет подводимого тепла совершается полезная работа, называется прямым циклом, или циклом тепловой машины (двигателя). Oн совершается по часовой стрелке и в P - v, и в T - s координатах.
Цикл, в котором наоборот, работа сжатия больше работы расширения, т.е. за счет затраченной работы от рабочего тела отводится теплота, называется обратным циклом или циклом холодильной установки. Он совершается против часовой стрелки.
1. Нулевой цикл
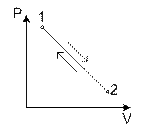
Рассмотрим процесс в P - v координатах.
 1-а-2:
1-а-2: 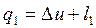
2-в-1: 
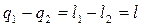
Величину l – называют работой цикла.
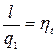 (7.1)
(7.1)
Формула (7.1) определяет термический КПД теплового двигателя. Эта величина определяет принципиальную возможность превращения тепла в работу.
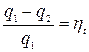 ;
; 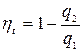 (7.2)
(7.2)
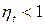 (7.3)
(7.3)
Формула (7.3) - следствие второго закона термодинамики
2. Холодильный цикл

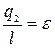 - холодильный коэффициент
- холодильный коэффициент
Прямой обратимый цикл Карно


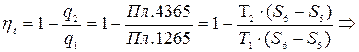
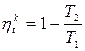 (7.5)
(7.5)
Формула (7.5) для КПД цикла Карно.
Рассмотрим произвольный цикл в том же интервале температур, что и цикл Карно.


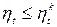 (7.6)
(7.6)

Теорема Карно. Термический КПД тепловой машины не зависит от вида рабочего тела и определяется только разностью температур источника тепла T 1 и приемника тепла Т2 (7.5). КПД любого цикла не может быть больше цикла Карно в том же интервале температур.
Пример :
1) Паровоз: t 1 = 200 °C, t 2 = 100 °C
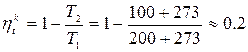 - это максимально возможный КПД.
- это максимально возможный КПД.
Внутренние потери учитывает эффективный КПД 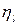 .
.
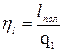 - эффективный КПД
- эффективный КПД 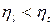
Для паровоза 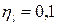
2) Тепловоз (ДВС, дизель) - 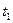 = 2000 ºС ,
= 2000 ºС , 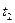 = 800 ºС
= 800 ºС
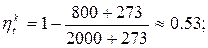
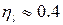
Обратный цикл Карно
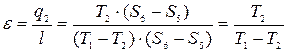 (7.7)
(7.7)

Формула (7.7) – для холодильного коэффициента
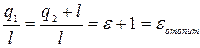 (7.8)
(7.8)
Формула (7.8) определяет отопительный коэффициент. Установка, использующая холодильный цикл для получения тепла, называется тепловым насосом.
Дата: 2018-12-21, просмотров: 1075.