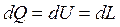(3.5)
Формула (3.5) выражает самое общее выражение первого закона термодинамики
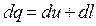(3.6)
(3.6) – первый закон, записанный через удельные величины
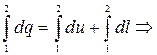
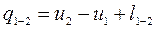(3.7)
Формула (3.7) - первый закон термодинамики для конечного процесса.
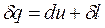(3.8)
Выражение (3.7) получено из (3.6) с учетом того, что теплота и работа – это функции процесса или, dq и dl не являются полными дифференциалами. Поэтому, вместо (3.6) часто записывают выражение (3.8), где d q и d l – просто бесконечно-малые величины, а не дифференциалы.
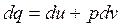(3.9)
(3.9) - первый закон термодинамики для случая, когда работа равна только работе изменения объема.
Энтальпия
Этот параметр широко используется в технике. Дадим сначала его математическое определение.
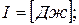
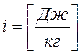
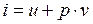- энтальпия (3.10)
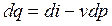- первый закон термодинамики через энтальпию (3.11)
Рассмотрим газ в цилиндре с поршнем. Давление газа уравновешивается
грузом G. Это позволяет выяснить физический смысл энтальпии
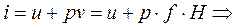
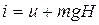
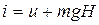(3.12)
Из формулы (3.12) следует, что энтальпия равна внутренней энергии данной системы плюс потенциальная энергия взаимодействия с окружающей средой. Сравнивая (3.11) и (3.9) и при этом учитывая (3.12) можно сделать вывод, что величина
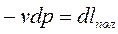(3.13)
имеет смысл работы.
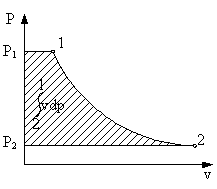Формула (3.13) представляет собой полезную (располагаемую) работу.
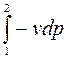
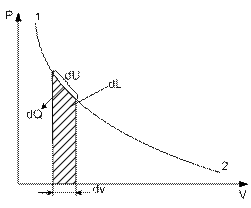
Таким образом, полезная работа в координатах (P-V) численно равна площади между кривой процесса и осью Р.
Теплоемкость
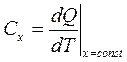(3.14)
Формула (3.14) - математическое определение теплоемкости, где х - условие процесса
3.7 Зависимость теплоемкости от количества вещества
1. Массовая - теплоемкость, отнесенная к одному килограмму масс.
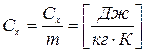
2. Объемная -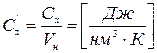 
3. Мольная - теплоемкость, отнесенная к одному молю газа
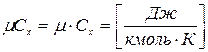
Связь теплоемкости с другими параметрами
(*)
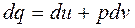
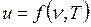
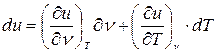Разделим (*) на dT:
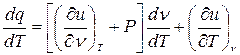
1. 
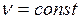
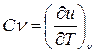(4.1)
Формула (4.1) справедлива для любого рабочего тела.
Для идеального газа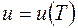 
.
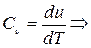
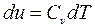(4.2)
Формула (4.2) справедлива только для идеального газа.
2. 
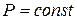
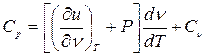(4.3)
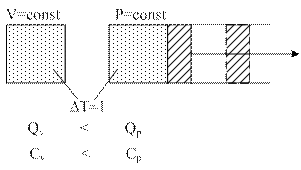
Формула (4.3) определяет теплоемкость Ср для любого рабочего тела и показывает, насколько Ср больше, чем Сv.
Идеальный газ.
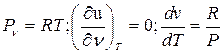
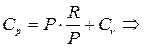
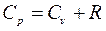(4.4)
Формула (4.4) выражает закон Майера.
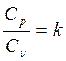- показатель адиабаты (4.5)
k зависит от числа атомов в молекуле газа:
k =1.67 - одноатомные газы;
k = 1.4 - двухатомные газы.
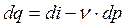
если взять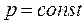 
, то 
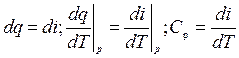
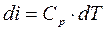(4.6)
(4.6) – для энтальпии.
Зависимость теплоемкости от температуры
Во всех вышеприведенных формулах используется истинная теплоемкость:
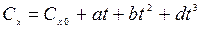
Введем понятие средней теплоемкости на некотором интервале изменения температуры.
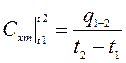(4.7)
Формула (4.7) определяет среднюю теплоемкость в интервале (t1, t2)
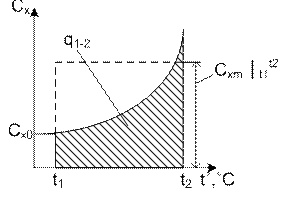
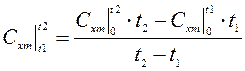(4.8)
(4.8) - рабочая формула для определения средней теплоемкости, при этом
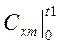и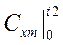 
берут из справочных таблиц.
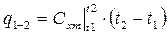(4.9)
(4.9) - расчетная формула для теплоты, в ней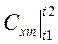 
находится по (4.8)
Теплоемкость смеси идеальных газов
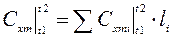(4.10)
(4.10) - массовая теплоемкость.
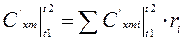(4.11)
(4.11) - для объемной теплоемкости.
Раздел 4 Второй закон термодинамики
Энтропия
Это одно из наиболее сложных понятий термодинамики. Физический
смысл его мы рассмотрим в дальнейшем, а пока дадим математическое определение.
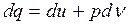
Рассмотрим частный случай идеального газа: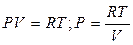 
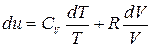(4.12)
Формула (4.12) не является полным дифференциалом, поэтому умножим левую и правую часть на интегрирующий множитель (1/Т)
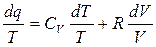(4.13)
(4.13) - полный дифференциал
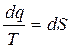(4.14)
(4.14) - здесь вводится новый параметр - S. Клаузиус назвал его энтропией. В переводе это означает - «преобразование»
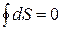(4.15)
Т.е. энтропия является функцией состояния, также как и внутренняя энергия.
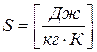
Энтропия является аддитивной величиной (экстенсивной), т.е. ее можно складывать. Пример аддитивных величин: S,U,V, m и др.
Величины, которые нельзя складывать, называют неаддитивными (интенсивными)
Пример: Т, Р, ρ, v.
Формулу (4.13) проинтегрируем:
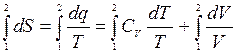, если 
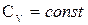, то
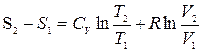(4.16)
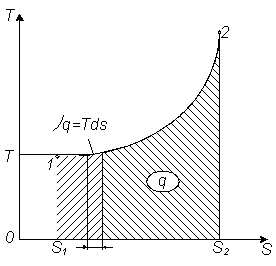
Формула (4.16) служит для вычисления изменения энтропии.
В координатах (T,S) площадь между кривой процесса и осью энтропии численно равна теплоте, поэтому такую диаграмму называют тепловой.
Дата: 2018-12-21, просмотров: 436.
