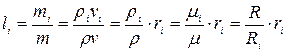(2.4)
1. 
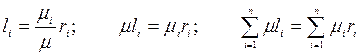
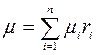- молекулярная масса смеси газа (2.5)
Пример 3. rО2 = 0,3 и rN 2 = 0,7
m = 32 × 0,3+28 × 0,7=9,6+19,6=29,2 кг/кмоль
Величина, определяемая по формуле (2.5) часто называется кажущейся молекулярной массой.
2. 
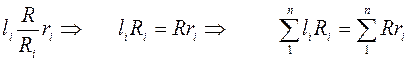
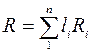- определение газовой постоянной смеси газа (2.6)
Реальные газы
Для реальных газов необходимо учитывать взаимодействие между молекулами, т.к. обычно это достаточно плотные газы.
Различные способы задания уравнения состояния реальных газов.
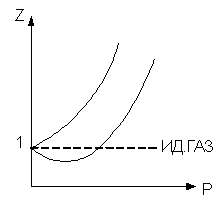
1 способ. Уравнение состояния с коэффициентом сжимаемости:
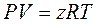(2.7)
Здесь z - коэффициент сжимаемости (иногда его называют сверхсжимаемостью газа).
Недостаток этого способа в том, что коэффициент z находится чисто экспериментально, притом он зависит не только от природы газа, но и от давления и температуры.
2 способ. Параметрические уравнения. Одно из первых таких уравнений:
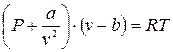- уравнение Ван-дер-Ваальса (2.8)
где a, b - параметры, которые зависят только от природы газа.
Это уравнение описывает свойства реальных газов с погрешностью 10¸20%.
В настоящее время появились аналогичные уравнения - Редлиха-Квонга, Пенга-Робинсона и т.д., которые дают меньшую погрешность.
3 способ. Уравнения с вириальными коэффициентами.
(2.9)
А,В,С - вириальные коэффициенты,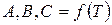 
Уравнение (2.9) считается наиболее точным для определения свойств реальных газов.
Помимо этих трех аналитических способов существуют графические методы расчета реальных газов с помощью различных диаграмм: Pv, Ts, Is.
Раздел 3 Первый закон термодинамики
Первый закон термодинамики - это закон сохранения энергии, записанный с помощью термодинамических понятий: внутренняя энергия, теплота, работа.
Внутренняя энергия
Под внутренней энергией в термодинамике понимают кинетическую энергию движения молекул, а также потенциальную энергию их взаимодействия.
|
|
Существенно, что другие виды энергии (химическая, ядерная) в конечном итоге превращается во внутреннюю энергию.
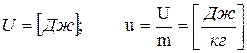
Внутренняя энергия является функцией состояния:
(3.1)
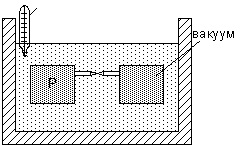Опыт Джоуля: в термостат поместили два сосуда, между которыми есть трубка с краном.
Из опыта Джоуля следует, что для идеального газа внутренняя энергия является функцией только температуры:
U = ¦ ( T ) (3.2)
3.2 Теплота
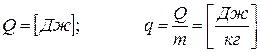
Энергия, предаваемая от одного тела к другому за счет разности температур, называется теплотой.
Содержать тело может только энергию, т.е. пока нет движения – нет теплоты.
3.3 Работа
Энергия, передаваемая от одного тела к другому при изменении объема этих тел или перемещение в пространстве, называется работой.
Как вычисляется работа рассмотрим на примере цилиндра с поршнем. Сначала для случая с постоянным, а затем с переменным давлением.
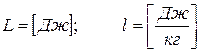
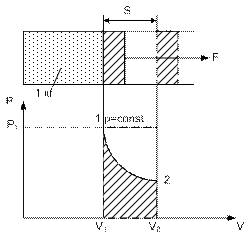
P = const
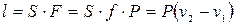
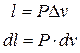(3.3)
Формула (3.3) – работа изменения объема
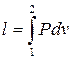- работа для конечного процесса (3.4)
Таким образом, в координатах P v работа численно равна площади между кривой процесса и осью объема. Работа, как и теплота, является функцией процесса.
Дата: 2018-12-21, просмотров: 582.
