Пример 291. В этом примере приводится ситуация, в которой в качестве обратной дуги, разрывающей контур, можно выбрать любую из двух (+, /) или (-, *).

DO 99 I = 2, N

X(I) = Y(I-1)*A(I)+Z(I)

Y(I) = X(I-2)/B(I)-W(I)

99 CONTINUE

Свернутый граф этого рекуррентного цикла будет иметь следующий вид :

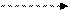
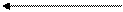
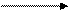
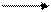
Y(I-1)            *            +             X(I)

A(I)                  Z(I)           2

X(I-2)                 /             -            Y(I)

B(I)               W(I) 

Рис. 80. Контур с двумя обратными дугами.

На вычисление T не влияет выбор разрываемой обратной дуги.

Теорема 61 . Пусть в свернутом графе тела цикла есть один контур. Пусть в этот контур входят несколько обратных дуг (A,A’), (B,B’), (C,C’) ... со сдвигами a, b, c,... соответственно. Предположим, что к началу каждой такой дуги A, B, C, ... от конца предыдущей ведет путь, состоящий из L(a), L(b), L(c),... дуг соответственно. Тогда минимальный интервал инициализации итераций конвейера не зависит от обратной дуги контура, которая считается разрываемой, и этот интервал равен

                   T = ](L(a)+L(b)+L(c)+...) / (a+b+c+...)[                 

Доказательство. Предположим, что контур разрывается дугой (A,A’). Тогда данные, вычисленные в вершине A, потребуются для использования в вершине A’ через a*T времени. С другой стороны, при вычислении исходные данные движутся от A’ к A следующее количество тактов (L(a)+L(b)+L(c)+...) – T*(b+c+...). Поскольку данные должны быть вычислены до необходимости их использования, для возможности синхронизации конвейера должно выполняться неравенство 

(L(a)+L(b)+L(c)+...) – T*(b+c+...) =< a*T

Из этого неравенства вытекает формула условия теоремы.

Полученная формула периода подачи данных известна для задач программной конвейеризации для суперкомпьютеров с архитектурой VLIW [89, с. 24]. Эта формула используется, как нижняя оценка интервала инициализации итераций. В случае архитектуры VLIW этот интервал инициализации итераций может быть увеличен, если у компьютера не достаточно ресурсов для выполнения тела цикла в соответствии с некоторым расписанием. Для суперкомпьютера с архитектурой перестраиваемого конвейера, если ресурсов не достаточно, то цикл не конвейеризуем и увеличение периода подачи данных не поможет, а, если ресурсов достаточно, то цикл конвейеризуется и полученная в теореме формула дает оптимальный период подачи данных. 

Теорема 62 . Если в свернутом графе много контуров, то в качестве периода чтения данных следует брать максимальную из величин интервалов, посчитанных для каждого контура. 

Доказательство. Очевидно, что величина периода подачи данных не может быть меньше такой величины, вычисленной для какого-либо одного из контуров графа. Достаточность рассматриваемой величины доказывается следующим алгоритмом синхронизации.

Алгоритм синхронизации конвейера выглядит следующим образом.

1. Вычисляем период подачи данных.

2. Разрываем все out-in дуги ( выходящие из генераторов)

3. Возвращаем по одной (в любом порядке) те разорванные дуги, которые не создают новых неориентированных циклов или ориентированных контуров.

4. Синхронизируем бесконтурный подграф свернутого графа, полученный из исходного.

5. Возвращаем по одной оставшиеся out-in дуги к рассмотренному графу с синхронизацией, в зависимости от следующих 2 случаев

a.  Если возвращаемая дуга создает неориентированные циклы, ставим на этой дуге буфер, синхронизирующий один из новых циклов. Остальные новые циклы окажутся синхронизированными автоматически, т.к. до добавления обратной дуги все пути от начала этой дуги к ее концу были на текущий момент синхронизированы. Следует оговорить корректность. Не умаляя общности, можно считать, что в этом случае возвращаемая дуга может входить в вершину с двумя входами (соответствующую бинарной операции). Тогда буфер следует поставить на одну из этих двух дуг. 

b. Если создаются ориентированные контуры, то достаточно буфером на возвращаемой дуге синхронизировать один из них, а остальные синхронизируются автоматически, т.к. до возвращения out-in дуги все пути от конца этой дуги к ее началу были на текущий момент синхронизированы.