Решетчатые графы использовались в методах распараллеливания программ с семидесятых годов в работах Л. Лампорта в методе гиперплоскостей [130], В. Вальковского в методе параллелепипедов [18] и методе пирамид [17] и у других исследователей. Эти графы использовались для иллюстрации идей, лежащих в основе методов распараллеливания. В явном виде эти графы не использовались, поскольку традиционные формы хранения графа в виде матрицы смежностей или в виде списка дуг не эффективны: прочтение такого графа может потребовать больше времени, чем последовательное исполнение программы, по которой этот граф построен. В конце 80-х годов был сделан прорыв в этом направлении: два математика В.В. Воеводин [25], [26], [27], [148] и P. Feautrier [124], [125], [123], [122] научились хранить этот граф в компактном виде, в виде функций, и разработали алгоритмы построения этих функций. У P. Feautrier функция строится для программ из линейного класса и содержит в своем определении не очень удобные для исследования условные операторы. У В.В. Воеводина функция является кусочно-линейной и определена на подмножестве линейного класса программ; но большинство практически значимых программ линейного класса относятся к этому подмножеству. В теории решетчатых графов можно отметить также работы [100], [110], [71].
Использование решетчатых графов в распараллеливающих компиляторах – одно из направлений исследований группы «Открытая распараллеливающая система» (ОРС). Эти исследования проводятся в следующих направлениях:
- Использование решетчатых графов в преобразованиях программ, которые не могут быть основаны на традиционном графе программных зависимостей.
- Использование решетчатых графов для отображения последовательных программ на параллельную архитектуру.
- Расширение класса программ, к которому применимы методы теории решетчатых графов.
Пусть в гнезде циклов имеется пара зависимых вхождений X(F(I)) и X(G(J)) и этой паре соответствует некоторая дуга графа зависимостей по данным. Зависимость означает обращение этих вхождений к одной и той же ячейке памяти. Но на разных итерациях гнезда циклов эти вхождения могут обращаться к разным ячейкам памяти. Возникает задача описания всех таких пар итераций гнезда циклов (I,J), для которых оба вхождения X(F(I)) и X(G(J)) обращаются к одной и той же ячейке памяти. Для описания этих пар итераций используется элементарный решетчатый граф программы.
Можно элементарный решетчатый граф определить не только для произвольной дуги информационной зависимости, а более общо, для произвольной упорядоченной пары вхождений X(F(I)) и X(G(J)) – если окажется, что эта пара не связана дугой графа информационных связей, то решетчатый граф будет пустым (без дуг).
Определение элементарного решетчатого графа. Пусть в гнезде циклов имеется пара зависимых вхождений X(F(I)) и X(G(J)) и этой паре соответствует некоторая дуга графа информационных связей. Через (F,G) будем обозначать элементарный решетчатый граф, построенный по двум вхождениям X(F) и X(G) переменной X в гнезде циклов. D - множество вершин этого графа – пространство итераций цикла (42). Дуга (I,J) принадлежит графу, если F(I)=G(J) , I<J (лексикографический порядок) и для любого такого K из области D, для которого K<J и F(K)=G(J), выполняется K =< I.
Иными словами, вершина I является лексикографическим максимумом множества всех таких точек K, для которых F(K)=G(J) и K<J. В [25] (F,G) называется элементарным решетчатым графом. Всякий раз при упоминании графа (F,G) будем предполагать, что индексные отображения F и G не содержат переменных, кроме счетчиков рассматриваемых объемлющих циклов – в этом случае граф (F,G) однозначно определен.
Описанный граф называется решетчатым, поскольку его вершины (точки пространства итераций) располагаются в узлах многомерной целочисленной решетки (размерность равна количеству циклов в гнезде).
Решетчатый граф строится по дуге графа информационных связей. Поскольку дуги графа информационных связей подразделяются на четыре типа зависимостей, решетчатые графы тоже имеют такие же типы: истинная (потоковая), анти-зависимость, выходная зависимость и входная зависимость.
Определение решетчатого графа истинной зависимости переменной Пусть задан фрагмент программы и некоторая переменная (м.б. индексная) X. Множество вершин решетчатого графа истинной зависимости переменной – это пространство итераций заданного фрагмента. Две точки пространства итераций I и J соединяются дугой, если
1. в графе информационных связей существует дуга истинной зависимости (u1, v1), решетчатый граф которой содержит дугу (I,J);
2. для любой другой дуги (u2, v1) истинной зависимости графа информационных связей, решетчатый граф которой содержит некоторую дугу (I2,J) , входящую в вершину J, точка пространства итераций I2 лексикографически меньше I, либо I2 = I, но вхождение u2 в тексте программы встречается всегда раньше вхождения u.
Аналогично определяются решетчатые графы переменной для антизависимости, выходной зависимости и входной зависимости.
Определение (полного) решетчатого графа фрагмента программы Решетчатый граф фрагмента программы – это граф, вершинами которого являются все точки пространства итераций, а множество дуг является объединением множеств дуг решетчатых графов всех переменных данного фрагмента.
Из определения решетчатого графа вытекает следующее свойство:
· в каждую вершину элементарного решетчатого графа входит не более одной дуги.
Из этого свойства вытекает возможность хранения решетчатого графа в виде отображения подмножества пространства итераций в пространство итераций: концу дуги решетчатого графа сопоставляется начало этой дуги.
Традиционные способы хранения графов в виде матрицы смежностей или списка дуг не приемлемы для решетчатых графов. Действительно, для гнезд циклов реальных долго считаемых программ количество дуг решетчатого графа может быть так велико, что прочтение всех дуг может потребовать время, сравнимое с временем последовательного выполнения исходной программы и распараллеливание, основанное на таком графе потеряет смысл.
Функция, описывающая решетчатый граф, может занимать объем, не зависящий от размерностей циклов, описывающих пространство итераций. Эта функция является кусочно-квазилинейной. «Квази-линейная» - это значит, что кроме линейных операций над счетчиками циклов эта функция допускает взятие целой части числа или условные операторы. Во многих практически важных случаях эта функция оказывается кусочно линейной.
Пример 264.
DO 99 I=1,N
DO 99 J=1,M
Y(I) =
= Y(J)
99 CONTINUE
В этом примере в точке пространства итераций с координатами (5,2) используется элемент Y(2) , который вычисляется на итерациях (2,1), (2,2), …, (2,M). Среди всех этих точек лексикографически самой старшей является точка (2,M). Таким образом, в элементарном решетчатом графе в точку с координатами (5,2) входит дуга из точки с координатами (2,M).
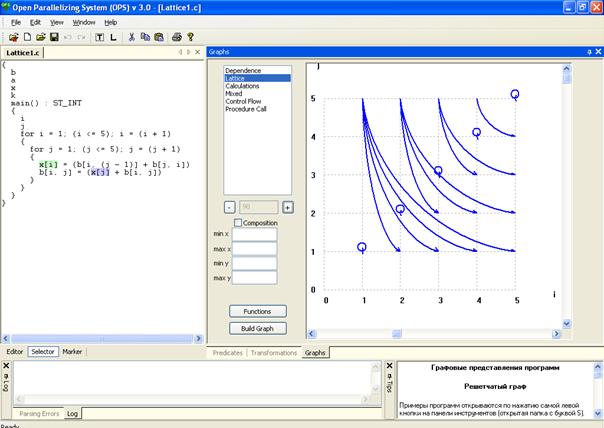
Рис. 65. Решетчатый граф построенный с помощью ОРС. Петли соответствуют циклически независимой зависимости.
Кусочно-линейная функция, описывающая решетчатый граф, автоматически построенная в ОРС:
Function:
i' = 5
j' = 5
Added Var(s)' Equation(s):
Definition Area:
-1*i+0*j <= -5
+1*i+0*j <= 5
+0*i-1*j <= -5
+0*i+1*j <= 5
Function:
i' = i +0
j' = j +0
Added Var(s)' Equation(s):
Definition Area:
-1*i+0*j <= -1
+1*i+0*j <= 4
+0*i-1*j <= -1
+0*i+1*j <= 4
-1*i+1*j <= 0
+1*i-1*j <= 0
Function:
i' = i -1
j' = 5
Added Var(s)' Equation(s):
Definition Area:
-1*i+0*j <= -2
+1*i+0*j <= 5
+0*i-1*j <= -1
+0*i+1*j <= 5
-1*i+1*j <= -1
+1*i-1*j <= 1
Function:
i' = j +0
j' = 5
Added Var(s)' Equation(s):
Definition Area:
-1*i+0*j <= -1
+1*i+0*j <= 5
+0*i-1*j <= -1
+0*i+1*j <= 5
-1*i+1*j <= -2
Конец примера.
При автоматическом выполнении преобразований программ необходимо контролировать эквивалентность этих преобразований. Для преобразований линейных участков и одномерных циклов эквивалентность таких преобразований выражается с помощью графа информационных связей. Для преобразований программ, содержащих многомерные циклы, обычно используют направление зависимости [139]. В данной работе для контроля эквивалентности будет использоваться решетчатый граф. Следующие два утверждения показывают связь между решетчатым графом и графом информационных связей.
Теорема 53 . В графе информационных связей цикла (42) существует дуга от генератора переменной X к использованию этой переменной (дуга истинной информационной зависимости), причем использование X(G) использует значение, записанное в память генератором X(F), тогда и только тогда, когда в графе (F,G) существует хотя бы одна дуга.
Доказательство вытекает непосредственно из определений графа (F,G) и графа информационных связей.
Теорема 54 . Пусть (X(F(I)), X(G(I))) – дуга истинной информационной зависимости в графе информационных связей и (F,G) – соответствующий решетчатый граф. Дуга (I,J) принадлежит графу (F,G) тогда и только тогда, когда в раскрутке цикла (42) вхождение X(G(J)) использует данное, записанное в память генератором X(F(I)).
Доказательство вытекает из определения графа (F,G) и определения раскрутки цикла.
Таким образом, существует взаимно однозначное соответствие между дугами графа (F,G) цикла (42) и существенными дугами графа информационных связей раскрутки. (Под существенной дугой понимается такая дуга истинной зависимости, для которой использование, соответствующее концу дуги, использует данные, записанные в память генератором, соответствующим началу дуги).
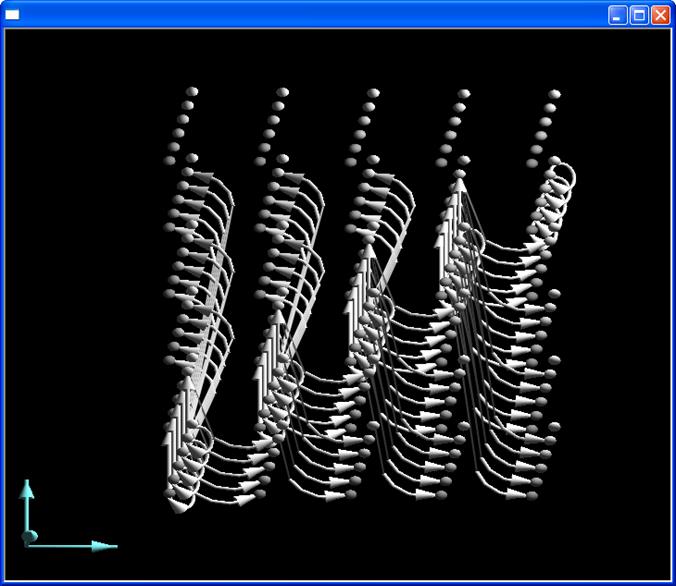
Рис. 66. Пример 3D визуализации трехмерного решетчатого графа
Дата: 2018-12-21, просмотров: 1142.