Наличие информационной зависимости означает, что какие-то вхождения должны обращаться к одной и той же ячейке памяти. Это не может не сказаться на алгоритме отображения цикла на архитектуру суперкомпьютера.
Далее будут рассматриваться только такие циклы, в которых для любой пары вхождений одной и той же переменной МОЖНО ОПРЕДЕЛИТЬ (имеющимися средствами) наличие или отсутствие информационной зависимости. В частности, будем полагать, что индексные выражения переменных линейно зависят от счетчиков объемлющих циклов.
Далее будем рассматривать циклы, которые не имеют нерегулярной информационной зависимости. Это ограничение необходимо для конвейеризации рекуррентного цикла и для возможности эффективного размещения данных при зависимости in-in [97].
Out-out зависимости означают запись в одну и ту же ячейку памяти. Для конвейеризации цикла эта зависимость должна быть исключена какими-либо преобразованиями или операции записи в одну ячейку памяти должны быть разведены во времени.
Out-in зависимости означают, что данное сначала записывается, а затем читается. Этот факт должен учитываться при конвейеризации.
In-in зависимости означают чтение из одной и той же ячейки памяти. Некоторые коммуникационные устройства позволяют одно считанное данное одновременно разослать в несколько, разных процессоров.
In-out – это дуга антизависимости, означающая, что из какой-то ячейки памяти сначала читается одно данное, а, затем, в эту ячейку записывается другое данное. Лучше всего от таких дуг избавиться известными предварительными преобразованиями.
Далее будем предполагать, что дуг антизависимости в цикле нет и коммутатор суперкомпьютера позволяет одно данное одновременно разослать в несколько устройств (процессоров или секторов памяти).
Циклически независимое OUT- IN склеивание. Рассмотрим граф вычислений линейного участка программы. Предположим, что на этом участке есть два вхождения переменной, связанные циклически независимой out-in зависимостью. Отождествим такую пару вершин, что первая вершина вычисляет данное, а вторая читает это данное из памяти, как это сделано в следующем примере.
Пример 282.
X = Y - A
Z = X + B
Граф вычислений этой программы состоит из двух компонент связности и имеет следующий вид:
time
1 2 3 4 5 6
Y - X X + Z
A B
Рис. 71. Два дерева для блока из двух операторов с циклически независимой зависимостью выхода первого и входа второго.
Пока первый оператор не запишет в память X, второй оператор не может считывать X из памяти. Операция вычитания имеет такой же результат, как и чтение из памяти переменной X. Поэтому можно результат вычитания сразу пересылать в суммирующий процессор:
1 2 3 4 5 6 time
Y - X
A + Z
B
Рис. 72. Результат склейки двух деревьев.
Полученный граф вычислений требует меньше времени для выполнения, чем исходный.
Циклически порожденное OUT- IN склеивание. Рассмотрим граф вычислений линейного участка программы. Предположим, что на этом участке есть два вхождения переменной, связанные циклически порожденной out-in зависимостью. Отождествим такую пару вершин, что первая вершина вычисляет данное, а вторая читает это данное из памяти, как это сделано в следующем примере.
Пример 283.
DO 99 I=3, N
X(I) = Y(I) - A
Z(I) = X(I-2) + B
99 CONTINUE
Граф вычислений этой программы состоит из двух компонент связности и имеет следующий вид:
time
1 2 3 4 5 6
Y(I) - X(I) X(I-2) + Z(I)
A B
Рис. 73. Два дерева с циклически порожденной зависимостью выхода первого и входа второго.
Пока первый оператор не запишет в память X(k), второй оператор не может считывать X(k) из памяти (но через две итерации цикла). Операция вычитания в этом примере имеет такой же результат, как операция чтения из памяти переменной X. Поэтому можно результат вычитания сразу пересылать в буфер суммирующего процессора. При этом получим следующий граф, в котором вес новой дуги, равен разности итераций:
1 2 3 4 5 6 time
Y(I) - X(I)
A 2
+ Z(I)
B
Рис. 74. Результат склейки с циклически порожденной зависимостью.
Временная функция должна доопределяется с графа вычислений на такой склеенный граф с учетом разности в итерациях.
Пример 284.
DO 99 I=3, N
X(I) = A(I)+B(I)
99 Z(I) = Y(I)+Z(I-1)*X(I-2)
Свернутый граф этого цикла будет иметь следующий вид:
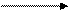
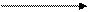A(I) + X(I)
2
B(I) 1
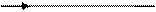
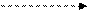
X(I-2) * + Z(I)
Z(I-1) Y(I)
Рис. 75. Свернутый граф цикла.
Здесь пунктирные дуги обозначают начальную загрузку процессора.
Из приведенного примера видно, что, если циклически порожденная out-in зависимость связана с рекуррентными вычислениями, то ей соответствует дуга свернутого графа, создающая контур, а если эта зависимость не связана с рекуррентными вычислениями, то контура в графе может и не быть.
Циклически независимое IN- IN склеивание. В этом параграфе также будем использовать тот факт, что коммутатор суперкомпьютера позволяет взять данное из одного сектора памяти и одновременно разослать его в несколько других процессоров. В частности, если какая-либо переменная встречается несколько раз подряд в качестве использования, то будем считать, что значение этой переменной достаточно прочесть из памяти один раз. Тогда из соответствующей вершины графа будет выходить несколько дуг и, следовательно, граф вычислений уже не будет деревом, хотя останется бесконтурным графом.
Пример 285. Для оператора присваивания a=b*c+b граф со склеенными вершинами выглядит следующим образом:
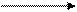
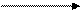
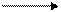
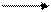
с * + a
b
Рис. 76. Склейка in-in зависимых вершин.
Не обязательно склеивать все вершины, читающие одно и то же данное. По этой причине по данному графу можно построить не единственный свернутый граф. Далее, когда будет идти речь о свернутом графе, можно будет понимать "какой-нибудь" свернутый граф.
Свернутый граф вычислений требует меньше операций чтения данных, чем исходный.
Возможность нескольких вариантов свернутого графа допускается для случая возможных последующих обобщений, которые могут потребоваться при введении ограничений на коммутатор.
Циклически порожденное IN- IN склеивание. Склеивание вершин графа происходит для вхождений, связанных регулярной in-in зависимостью. Вхождения, соответствующие таким вершинам, обращаются к памяти за чтением одних и тех же данных (in-in-сокращение).
Алгоритм склеивания вершин, связанных регулярной in-in зависимостью состоит из трех частей:
1. Строим неориентированный граф регулярных in-in зависимостей (вершины этого графа - вхождения, а ребро соединяет две вершины тогда и только тогда, когда эти вхождения связаны регулярной информационной зависимостью типа in-in).
2. Каждую компоненту связности графа регулярных in-in зависимостей следует разбить на наименьшее количество частей так, чтобы для любых двух вершин каждой части при склеивании этих вершин не получалось дуги графа вычислений длиннее чем размер буфера.
3. Вершины каждой из полученных частей склеиваем.
В этом алгоритме пункты 1 и 3 могут быть реализованы несложным образом, а на пункте 2 остановимся подробнее.
Каждая компонента связности графа регулярных in-in зависимостей соответствует вхождению одной и той же переменной. Пусть данная компонента связности соответствует массиву X. Не умаляя общности, будем считать, что массив X одномерный. Каждой вершине v, соответствующей вхождению переменной X(I+b), поставим в соответствие число g(v) = b (ввиду регулярности зависимостей, для всех вхождений величина a одинакова). Расположим все вершины в порядке неубывания функции g. Пусть v1 – первая из них (с наименьшим значением g). Пусть h – размер буфера. Тогда к первой части отнесем все те вершины vk, для которых g(vk) – g(v1) ≤ h. Отбросив первую часть, аналогичным образом построим вторую и т.д. Очевидно, что данный алгоритм оптимален по качеству разбиения и по быстродействию.
Пример 286.
DO 99 I = 1, N
99 Y(I) = X(I)... X(I-1)... X(I-9)... X(I-5)... X(I+9)... X(I+3)... X(I+11)
v1 v2 v3 v4 v5 v6 v7
Пусть размерность буфера h равна 8. Тогда все семь вхождений можно разбить на три группы: первая – v3, v4, v2; вторая – v1, v6; третья – v5, v7.
Приведенный алгоритм склеивания вершин более актуален для упоминавшегося случая, при котором различные операции имеют задержки различной длины.
Описанное в данном параграфе склеивание не является необходимым. Если не пользоваться таким склеиванием, то в дальнейшем, при конвейеризации может понадобиться больше операций чтения данных и, возможно, копирование одного массива в различных секторах памяти.
Дата: 2018-12-21, просмотров: 529.
