Можно выделить следующие виды параллельных вычислений:
· Параллельное выполнение задач.
· Параллельное выполнение функций.
· Параллельное выполнение блоков.
· Параллельное выполнение циклов.
· Параллельное выполнение операций.
· Параллельное выполнение микрокоманд.
Параллельное выполнение задач – это функции операционной системы. Параллельное выполнение микрокоманд реализуется, как правило, аппаратно. Другие виды параллельных вычислений возлагаются либо на программиста, либо на распараллеливающий компилятор.
Под распараллеливанием понимается преобразование последовательной программы в параллельную. Таким образом, распараллеливание можно рассматривать, как частный случай оптимизации программ, и относиться к теории преобразования программ. Распараллеливание зависит от вычислительной архитектуры, на которой программы должны выполняться. Но одни и те же преобразования программ могут оказаться полезными для различных архитектур.
Параллельное выполнение функций и блоков предполагает асинхронную архитектуру MIMD (Many Instruction Multiple Data). Параллельное выполнение операций (иногда называют параллельным выполнением линейных участков) реализуется в архитектурах VLIW (Very Long Instruction Word) или суперскалярных. Циклы распараллеливаются на MIMD, SIMD (Single Instruction Multiple Data), конвейерные архитектуры.
У человека, который только приступает к параллельному программированию, возникают некоторые априорные представления об этой деятельности – гипотезы. Как правило, неверные. Приведем примеры.
Гипотеза 1. Если вычислительная система состоит из N параллельно работающих вычислительных устройств, то последовательная программа может быть выполнена в N раз быстрее.
Опровержение вытекает из понятной для школьников задачи о том, что сумму N чисел невозможно вычислить даже всем классом быстрее, чем за log2(N) шагов. И это притом, что не учитывается расход времени на обмены данных.
То, как успех распараллеливания зависит от исходного алгоритма, иллюстрирует следующая задача.
Задача. Предположим, что некоторая задача решается алгоритмом сложности 2 n, то есть, при количестве данных на входе n алгоритму требуется 2 n операций для решения задачи на однопроцессорном компьютере (существует много сотен таких практически значимых алгоритмов для решения NP-полных задач). Для n=100 однопроцессорный компьютер работает 1 час. Для какого значения n сможет решить задачу за 1 час двухпроцессорный компьютер? (Ответ: n = 101).
Изучение параллельного программирования начинается с параллельных вычислительных архитектур. Здесь никак нельзя обойти SIMD и MIMD. В архитектуре SIMD все вычислительные устройства ведут одинаковые вычисления, а MIMD позволяет проводить разные вычисления. Это повод для следующей «очевидной» гипотезы.
Гипотеза 2. Всякий векторизуемый цикл может быть выполнен асинхронно.
Опровержение. Векторное выполнение следующего цикла равносильно его последовательному выполнению.
For I = 1 to N do
X[i] = 2*X[i+1]
Асинхронное параллельное выполнение этого же цикла может дать и другие результаты, например, если вторая итерация завершится до начала первой итерации.
Иногда используется упрощенная формулировка о том, что асинхронное параллельное выполнение процессов – это выполнение «в любом порядке». Здесь появляется еще одна «очевидная» гипотеза.
Гипотеза 3. Пусть программа F представляет собой последовательное выполнение двух фрагментов F1 и F2 . Предположим, что последовательное выполнение этих фрагментов в произвольном порядке не влияет на результат. Тогда эти фрагменты можно выполнять асинхронно.
Опровержение. Пусть оба фрагмента F1 и F2 одинаковы и имеют вид
{
X = 1;
Y = X;
X = 2;
}
Перестановка местами одинаковых фрагментов, очевидно, является эквивалентным преобразованием (просто не меняет программу). Но параллельное асинхронное выполнение этих фрагментов некорректно. Действительно, при последовательном выполнении программы переменная Y приобретает значение 1. Но, если операторы в процессах выполняются по расписанию из следующей таблицы, то по окончании параллельного исполнения значение переменной Y будет равно 2.
| Номер процесса Время В тактах | 1 | 2 |
| 1 | X = 1 | X = 1 |
| 2 | Y = X | |
| 3 | X = 2 | |
| 4 | Y = X | |
| 5 | X = 2 |
Из приведенных гипотез можно сделать выводы о том, что эвристические соображения следует подкреплять математическими доказательствами, и при преобразовании последовательных программ в параллельные следует анализировать программные зависимости.
При распараллеливании программ наиболее часто распараллеливаются циклы. С одной стороны это связано с тем, что наиболее долго в программах выполняются гнезда циклов. С другой стороны, под параллельным выполнением циклов обычно понимается одновременное выполнение итераций этого цикла, а различные итерации цикла отличаются только значениями счетчика цикла. Одинаковость параллельно выполняемых процессов (итераций цикла) при синхронном распараллеливании (SIMD) просто необходима, но и при асинхронном распараллеливании тоже существенна, поскольку такие процессы имеют шанс выполняться примерно одинаковое время, обеспечивая этим самым примерно одинаковую загрузку вычислительных устройств.
Но, оказывается, на разных вычислительных архитектурах могут параллельно вычисляться разные циклы. Термин «одновременное» допускает различные толкования и требует дополнительных пояснений. Распараллеливанию циклов могут мешать программные зависимости. Если в цикле есть только операторы присваивания и нет никаких информационных зависимостей, то итерации такого цикла можно выполнять независимо на любой из описанных типов архитектур. Разные вычислительные архитектуры допускают разные типы зависимостей.
В ОРС автоматически определяются параллельно выполняемые циклы для различных вычислительных архитектур. Для определения параллельно выполняемых циклов следует щелкнуть мышью по кнопке «маркер» под левым верхним окном на экране ОРС.
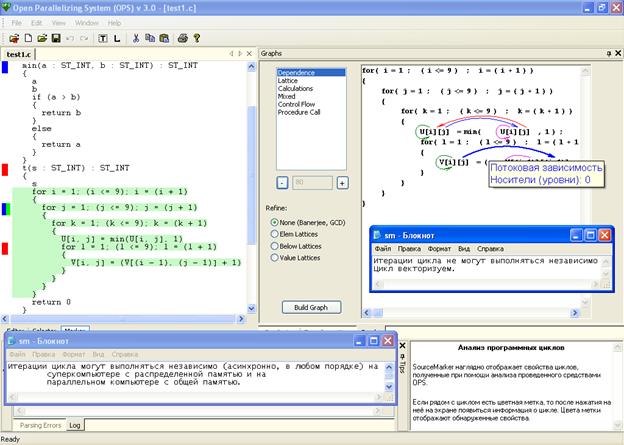
Рис. 67. Отображение свойств циклов и функций в ОРС. Правое информационное окно сообщает о векторизуемости самого вложенного цикла. Нижнее информационное окно говорит о возможности независимого выполнения итераций второго цикла сверху. Синяя метка возле описания функции min() говорит о том, что эта функция не имеет побочных эффектов, которые могли бы препятствовать распараллеливанию циклов, содержащих вызов этой функции.
Одна из важных характеристик вычислительной архитектуры – общая (shared) или распределенная (distributed) память. Общая память допускает входные зависимости. Входная зависимость означает, что разные итерации цикла используют одни и те же данные. При распределенной памяти входная зависимость мешает, но может быть устранена предварительной рассылкой данных.
Распараллеливанием цикла называется замена цикла
DO 99 I=L,N,h
99 ТЕЛОЦИКЛА(I)
циклом
DO ALL 99 I=L,N,h
99 ТЕЛОЦИКЛА(I)
Здесь оператор параллельного цикла DO ALL означает инструкцию для параллельного компьютера, требующую одновременного выполнения ТЕЛОЦИКЛА(I) для всех значений счетчика I, указанных в заголовке цикла (предполагается, что для каждого значения счетчика цикла I ТЕЛОЦИКЛА(I) будет выполняться в своем процессорном элементе).
В общем случае ТЕЛОЦИКЛА(I) может содержать любые операторы, в том числе и другие циклы. Семантика оператора DO ALL зависит от вычислительной архитектуры. Иногда вместо DO ALL оператор параллельно выполняемого цикла обозначают DO SIM (SIMULTANIOUSLY), DO PAR, ParDO, DO Concurrently.
Распараллеливание, как преобразование, состоящее в замене заголовка последовательного цикла заголовком параллельного, тривиально. Вопрос в том, когда такое преобразование эквивалентно и в том, чтобы вспомогательными преобразованиями привести цикл к виду, в котором распараллеливание является эквивалентным преобразованием.
Векторизация циклов
Векторные компьютеры позволяют эффективно выполнять операции над векторами: найти сумму двух векторов, произведение вектора на число, и др. Наиболее известный векторный компьютер Cray-1 много лет занимал лидирующее место по производительности среди суперкомпьютеров. Этот компьютер обрабатывал векторы длины 64. В СССР тоже разрабатывались векторные суперкомпьютеры ПС-3000 и др. Для Cray-1 и для ПС-3000 разрабатывались распараллеливающие компиляторы.
Последовательные циклы, допускающие замену на векторную команду, называются векторизуемыми, а сама такая замена – векторизацией. Векторизуются циклы, которые содержат только операторы присваивания. Векторизация является эквивалентным преобразованием при дополнительных ограничениях на информационные зависимости в цикле. Для описания этих ограничений понадобятся дополнительные понятия.
Будем говорить, что вхождение V1 расположено в программе раньше вхождения V2, а вхождение V2 расположено позже вхождения V1, если при любом исполнении программы обращение к вхождению V1 происходит по времени раньше, чем обращение к вхождению V2.
Если вхождения V1 и V2 принадлежат операторам одного и того же линейного участка программы, то V1 расположено раньше V2 тогда и только тогда, когда выполняется одно из условий: 1) V1 принадлежит оператору с меньшим номером, чем V2, 2) V1 и V2 принадлежат одному и тому же оператору присваивания, причем V2 является генератором, а V1 - использованием.
Лемма 3. Пусть в теле цикла все операторы являются операторами присваивания и вхождения V1 и V2 обращаются к одной и той же ячейке памяти. Пусть V1 расположено в тексте программы раньше, чем V2. Тогда после векторизации вхождение V1 будет обращаться к памяти раньше, чем V2.
Доказательство вытекает из того, что после векторизации сначала к памяти будет обращаться вхождение V1 для всех значений счетчика цикла, а спустя некоторое время V2 (тоже для всех значений счетчика цикла).
Пример 265.
DO 111 I = 1, N
A(I) = B(I)+C(I)
D(I) = A(I+1)/2.
111 CONTINUE
В этом цикле вхождение A(I+1) обращается к ячейке памяти A(2) раньше, чем вхождение A(I), но после распараллеливания будет наоборот.
DO ALL 111 I = 1, N
A(I) = B(I)+C(I)
D(I) = A(I+1)/2.
111 CONTINUE
Конец примера.
Теорема 57 . Пусть в теле цикла все операторы являются операторами присваивания. Пусть в графе информационных связей тела цикла все дуги направлены от вхождений, которые встречаются раньше к вхождениям, которые в тексте расположены позже. Тогда векторизация данного цикла является эквивалентным преобразованием.
Доказательство. При векторизации изменяется только последовательность исполнения операций. Поэтому эквивалентность может быть нарушена только в том случае, когда при векторизации меняется последовательность обращения различных вхождений к одной и той же ячейке памяти. Если два вхождения обращаются к одной и той же ячейке памяти, то в графе информационных связей они соединяются дугой. Поскольку в теле цикла дуги графа информационных связей направлены от вхождений, которые расположены раньше к вхождениям, расположенным позже, порядок обращения вхождений к памяти при векторизации не меняется.
Следствие. Если цикл векторизуется, то он может быть разбит на циклы, в каждом из которых по одному оператору присваивания.
Пример 266. Следующий цикл имеет рекуррентную зависимость и, поэтому не векторизуется.
DO 111 I = 1, N
X(I) = A(I)*X(I-1)+B(I)
111 CONTINUE
Конец примера.
Может случиться, что цикл непосредственно не векторизуется, а после некоторых вспомогательных преобразований станет векторизуемым. Это, как правило, те же вспомогательные преобразования, которые используются при разрезании цикла. Рассмотрим такие примеры.
Пример 267. Следующий цикл имеет дуги зависимости, направленные снизу вверх и, поэтому не векторизуется. Но после перестановки операторов местами цикл становиться векторизуемым.
DO 111 I = 1, N
X(I) = A(I)*Y(I-1)+B(I)
Y(I) = D(I)/X(I+1)
111 CONTINUE
Конец примера.
Пример 268. Следующий цикл содержит вхождения переменной X, которая не зависит от счетчика цикла. Эти два вхождения связаны двумя дугами, направленными в противоположные стороны.
DO 111 I = 1, N
X = A(I)*Y(I)+B(I)
Y(I) = D(I)/X
111 CONTINUE
Преобразование «растягивание скаляров» может удалить одну из этих дуг (антизависимость), после чего цикл станет векторизуемым.
DO 111 I = 1, N
XX(I) = A(I)*Y(I)+B(I)
Y(I) = D(I)/XX(I)
111 CONTINUE
X = XX(N)
Конец примера.
Пример 269. Следующий цикл имеет две дуги антизависимости, одна из которых направлена снизу вверх, а другая, наоборот, сверху вниз. По этой причине цикл не векторизуется и перестановка операторов местами не приводит к векторизуемости.
DO 111 I = 1, N
X(I) = A(I)*Y(I+1)+B(I)
Y(I) = D(I)/X(I+1)
111 CONTINUE
Введение временного массива приводит данный цикл к векторизуемому виду.
DO 111 I = 1, N
TEMP(I) = X(I+1)
X(I) = A(I)*Y(I+1)+B(I)
Y(I) = D(I)/TEMP(I)
111 CONTINUE
Конец примера.
Дата: 2018-12-21, просмотров: 894.