Будем рассматривать систему уравнений с ленточной двухдиагональной матрицей следующего вида

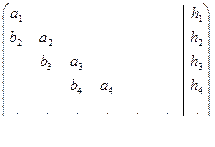
Ясно, что эта система имеет единственное решение тогда и только тогда, когда все элементы главной диагонали отличны от нуля. В этом случае каждое i-ое уравнение можно разделить на 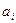. Все эти деления можно выполнить одновременно. В результате задача сведется к решению системы уравнений с матрицей следующего вида.

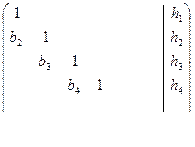                                                                  (32 )

       Параллельный алгоритм решения такой системы уравнений состоит в следующем. На первом шаге следует одновременно получить нули на месте элементов b(I). Для этого из каждой I-ой строки надо вычесть предыдущую, умноженную на число b(I). При этом все элементы поддиагонали станут нулевыми, но элементы второй поддиагонали окажутся ненулевыми.

~   ~ 

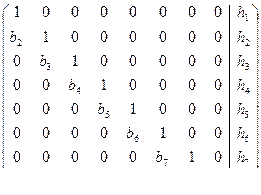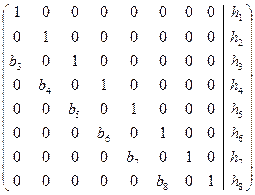На втором шаге из каждой I-ой строки надо вычесть строку с номером (I-2), умноженную на число b(I). При этом все элементы второй поддиагонали станут нулевыми, но элементы в четвертой поддиагонали окажутся ненулевыми.

~     

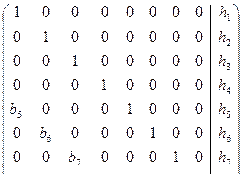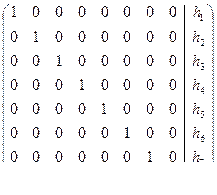
На k-ом шаге из каждой I-ой строки надо вычесть строку с номером I-2**(k-1), умноженную на число b(I). При этом, все элементы поддиагонали с номером 2**(k-1) станут нулевыми, но элементы поддиагонали с номером 2**k окажутся ненулевыми. Через ]log(N)[ шагов матрица системы станет единичной и в правой части будет получен вектор-решение (здесь и далее логарифмы берутся по основанию 2 и операция ]a[ означает наименьшее целое, не меньшее числа a). 

Заметим, что в этом алгоритме ненулевая поддиагональ после каждого шага оказывается вдвое дальше от главной диагонали, чем перед этим шагом. Описанный алгоритм можно записать в виде небольшой программы на фортране.

       do 99 k = 1, ]log(N)[

       do 99 I = 2**(k-1)+1, N

       h(I)= h(I) - b(I)*h(I-2**(k-1))                                                    (33 )

99   b(I) = - b(I)*b(I-2**(k-1))

Следует обратить внимание, что операторы присваивания в этом цикле нельзя менять местами – их следует выполнять именно в том порядке, в каком они записаны.

Все итерации внутреннего цикла могут выполняться одновременно (параллельно). Это возможно на суперкомпьютерах с векторной, SIMD или MIMD архитектурами. Кроме того, внутренний цикл может быть выполнен на конвейерной архитектуре. Объемлющий цикл не распараллеливается (его итерации нельзя выполнять одновременно) ввиду выходной зависимости по данным.

       Для верхнетреугольных двухдиагональных матриц алгоритм решения системы уравнений выглядит аналогичным образом.

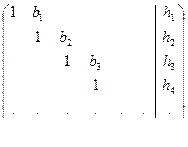
       do 99 k = 1, ]log(N)[

       do 99 I = 1, N - 2**(k-1)

       h(I)= h(I) - b(I)*h(I+2**(k-1))

99   b(I) = - b(I)*b(I+2**(k-1))

О распараллеливании этого алгоритма справедливы все слова, написанные для случая нижнетреугольных матриц.

Описанный выше алгоритм можно применить для параллельного вычисления многочлена

f(x) = a₀xⁿ + a₁x^n-1 + … + a_n-1x +a_n

Для этого достаточно решить систему, n-ый корень которой равен значению этого многочлена в точке x.

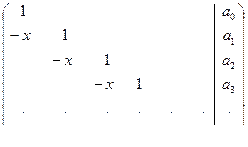
Для одновременного вычисления всех n сумм квадратных матриц

A₁

A₁ + A₂

A₁ + A₂ + A₃

………………….

 A₁ + A₂ + A₃ +…+ A_n

достаточно параллельно решить блочную систему уравнений, корнями которой являются эти суммы

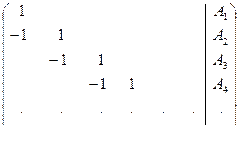
Для одновременного вычисления всех произведений квадратных матриц

A₁

A₁ * A₂

A₁ * A₂ * A₃

………………….

 A₁ * A₂ * A₃ *…* A_n

достаточно параллельно решить блочную систему уравнений, корнями которой являются эти произведения

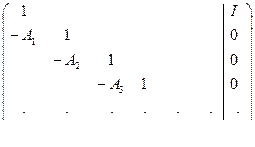
Последние две задачи рассматривались в [25]