Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Под КПД трансформатора понимается отношение активной мощности отдаваемой в нагрузку к активной мощности, потребляемой от сети [1]:       

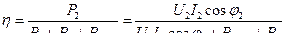                            ,           (2.30)

где P_c – потери в сердечнике (динамические  и статические);

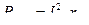 – потери в обмотках (  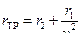– сопротивление                                           обмоток, приведённое к  вторичной цепи).

     Трансформатор может работать не только в номинальном режиме. Для оценки степени загрузки трансформатора по току вводят понятие коэффициента загрузки 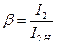, где I_2Н –  номинальный ток трансформатора. Тогда  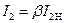и (2.30) принимает вид

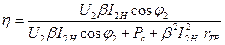                                                               (2.31)

Потери в сердечнике P_c – не зависят от коэффициента загрузки β ( то есть от тока I ₂ , это потери холостого хода ).

Если исследовать (2.31) на экстремум по β, то  КПД будет иметь максимум ( 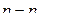)  при 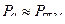, что соответствует β_ОПТ = 0,5…0,6. На рис. 2.28 показана зависимость этих потерь и КПД от .

                            

                  

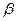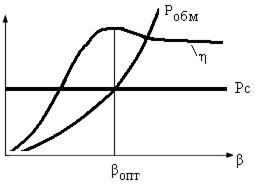
Рисунок 2.28 – Зависимость КПД от коэффициента загрузки

 

     Потери в обмотках пропорциональны квадрату коэффициента загрузки. При постоянной нагрузке устанавливают β = 1, что выполняется в маломощных трансформаторах. В мощных трансформаторах при изменяющейся  нагрузке выбирают β ≈ β_ОПТ, что соответствует наименьшим потерям. Крутизна этой зависимости невысокая, максимум выражен слабо и, поэтому, условие 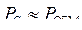 не является строгим. Для примера приведём практические значения КПД и коэффициента мощности ( 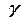) для маломощных трансформаторов при частоте  50 Гц. Они представлены на рис. 2.29 [31]. 

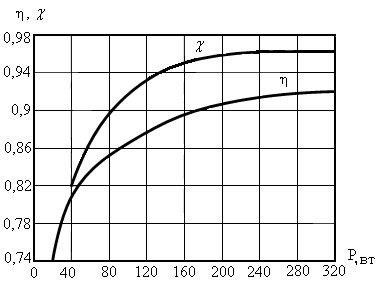
Рисунок 2.29 – Зависимость КПД и коэффициента мощности от

выходной мощности трансформатора

 

На рисунке 2.29 буквой Р обозначена активная мощность нагрузки трансформатора. Видно, что с ростом выходной мощности растут и энергетические показатели трансформатора.

Мощность трансформатора

При проектировании трансформаторов исходной является мощность, которая связывает габариты трансформатора с  полной мощностью нагрузки:

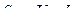                                                                                             (2.32)

Полная (полезная) мощность многообмоточного трансформатора, есть сумма полных мощностей всех  его вторичных обмоток:

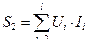                                                                                           (2.33)

При активной нагрузке  мощность активна и равна Р_2.

Типовой (габаритной) мощностью трансформатора называют полусумму мощностей всех его обмоток

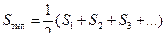                                                                           (2.34)

    Найдём типовую мощность для  двухобмоточного  трансформатора.

    Полная мощность первичной обмотки  (U₁, I₁ – действующие значения) – эта мощность определяет габариты обмоток: число витков –входным напряжением, а сечения проводов – действующими токами. Габаритная мощность трансформатора (типовая) определяет реальное сечение сердечника – s_с и равна

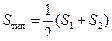                                                                                             (2.35)

Учитывая, что 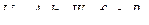, где s – теоретическая площадь поперечного сечения магнитопровода ( стали ). Реальная площадь сечения обычно меньше и зависит от толщины пластин (ленты), поэтому вводят, так называемый коэффициент заполнения сердечника – отношение реальной площади сечения к геометрической 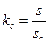, которую легко измерить. Величина  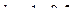( зависит от толщины ленты).  Для прессованных сердечников . 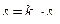Таким образом,  и выражение для напряжения первичной обмотки принимает вид

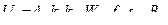                                                           (2.36)

Аналогичное выражение можно записать и для вторичной обмотки, а мощности первичной обмотки и типовая соответственно равны 

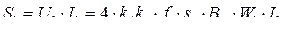                                        (2.37)

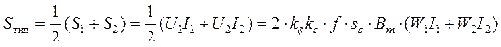          (2.38)

Отношение тока в обмотке к сечению проводника называется плотностью тока и для всех обмоток трансформатора она одинакова.

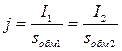                                                    ,                                                (2.39)

 где  s _обм1, s_обм2 – площади сечения проводников обмоток.

Заменим ток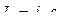и   и 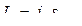, тогда сумма в скобках в (2.38) равна .

где s_м –  сечение всех проводников (меди) в окне магнитопровода, как показано на рисунке 2.30.

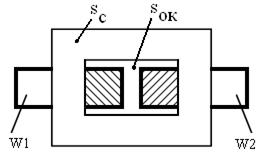
Рисунок 2.30 – К выводу формулы габаритной мощности

трансформатора

 

Введём коэффициент заполнения окна медью 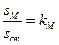. Его величина находится в пределах  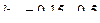и зависит от толщины изоляции проводов, каркаса, межслойной изоляции, способа намотки и пр. Тогда 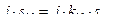 и выражение для типовой мощности принимает окончательный  вид

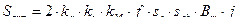                                                                  (2.40)

Из выражения (2.40) следует, что типовая мощность определяется произведением . При увеличении линейного размера трансформатора в m раз, его объём (масса) увеличится в m ³ раз, а мощность возрастёт в m ⁴ раз. Поэтому, удельные массо-объёмные показатели трансформаторов улучшаются с увеличением габаритной мощности. С этой точки зрения предпочтительны многообмоточные трансформаторы по сравнению с несколькими двухобмоточными.

     При конструировании трансформаторов следует стремиться к увеличению коэффициента заполнения окна магнитопровода обмотками – 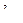, так как  повышается S_тип. Для этого используют провода прямоугольного сечения.

     Выражение (2.40) является основой для расчёта трансформатора. Его преобразуют к виду:

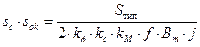                                                                            (2.41)

По заданной выходной мощности (S_тип) находят произведение   и по справочнику выбирают тип и размер магнитопровода, у которого произведение 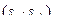 больше или равно найденному из (2.41). Такой сердечник обеспечит требуемую мощность в нагрузке.

Трёхфазные трансформаторы

     Трёхфазные системы были разработаны русским электриком М.О. Доливо-Добровольским (1862 – 1919 гг.). Они широко распространены в энергетике и представляют собой симметричную трёхфазную систему напряжений промышленной частоты, сдвинутых между собой на электрический угол 120⁰. Схематическое изображение источников трёхфазных напряжений (генераторов) показано на рисунке 2.31, где начала фаз обозначены латинскими буквами ABC, а концы фаз буквами XYZ (или условно можно обозначить точками вместо букв ).  

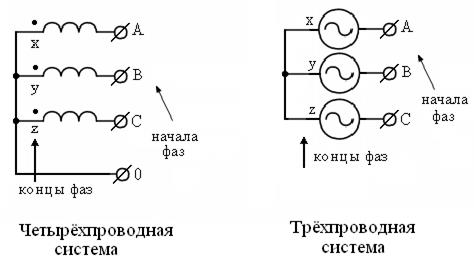
Рисунок 2.31 – Схематическое изображение источников трёхфазных

напряжений

 

На рисунке 2.32 показаны временное и векторное представления трёхфазной системы напряжений.

 

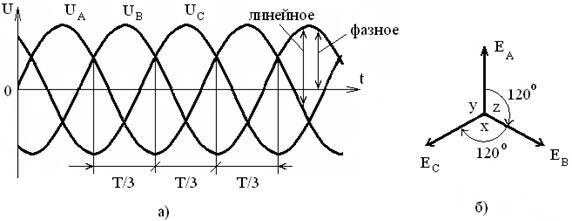
Рисунок 2.32 – Временное (а) и векторное (б) представление трёхфазной

системы напряжений

 

На этом рисунке Т – период, Е – фазная ЭДС. Мгновенные значения фазных ЭДС соответственно равны

                

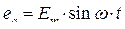
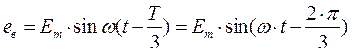                                           (2.42)

                

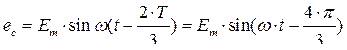
Это симметричная трёхфазная система, в которой в любой момент времени выполняется равенство          

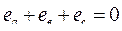                                                                                              (2.43)

Чередование фаз принято условно положительным по часовой стрелке. Существуют три основные схемы соединения в трёхфазных цепях: звезда, треугольник и зигзаг , но наиболее широко известны первые две – звезда  и треугольник (говорят соединение в звезду или в треугольник). Рассмотрим их. На рис.2.33 приведена схема соединения источника и нагрузки звездой.

 

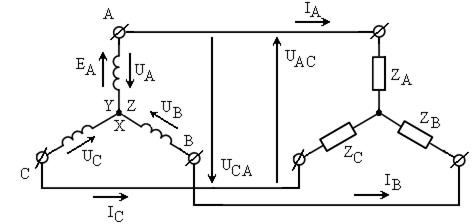
Рисунок 2.33 – Схема соединения источника и нагрузки звездой

 

На этом рисунке  – фазные напряжения. Проводники, идущие от начал фазных обмоток к нагрузке называют линейными проводами (линия). Соответственно напряжения между проводами называют линейными (например, U_AC   и U_CA). Очевидно, что здесь линейный ток равен фазному, а линейное напряжение превышает фазное в корень из трёх раз, поскольку линейное напряжение равно геометрической разности фазных напряжений (см. рис.2.32 ).

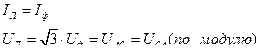                                                           (2.44)

На рис.2.34 приведена схема соединения источника и нагрузки треугольником.

 

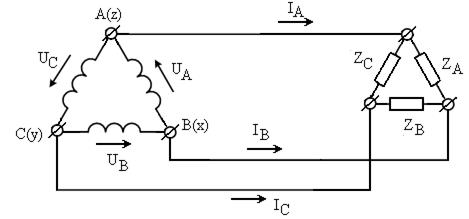
Рисунок 2.34 – Схема соединения источника и нагрузки треугольником

При таком соединении линейные напряжения равны фазным, а линейные токи превышают фазные в корень из трёх раз, поскольку они складываются из фазных.

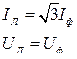                                                                                                   (2.45)

    Мощность в трёхфазной цепи не зависит от схемы соединения и складывается из мощностей отдельных фаз.

Активная мощность:

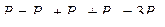                                                                                               (2.46)

Реактивная мощность:

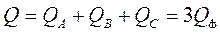                                                                             (2.47)

Полная мощность:

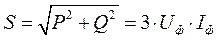                                                                            (2.48)

Можно перейти к линейным токам и напряжениям.

Так, при соединении звездой получаем:

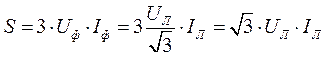                                                                  (2.49)

При соединении треугольником: 

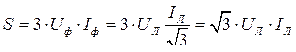                                                               (2.50)

То есть, действительно не зависит от схемы соединения.

Трансформацию трёхфазного напряжения можно осуществлять двумя способами:

–   тремя отдельными однофазными трансформаторами, как показано на рисунке 2.35а. Это, так называемый, групповой трансформатор. 

– одним трёхфазным трансформатором с общей магнитной системой (рис.2.35б).

 

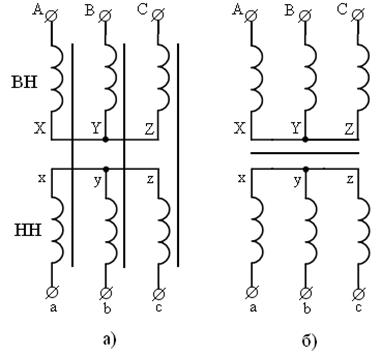
Рисунок 2.35 – Условное обозначение группового (а) и трёхфазного (б)

трансформаторов при включении звезда-звезда

 

Первичные обмотки трансформатора называются обмотками высшего напряжения (ВН) и обозначаются заглавными буквами, а вторичные обмотки называются обмотками низшего напряжения (НН) и обозначаются малыми буквами. Первичные и вторичные обмотки соединяются любым способом.  

 Соединение в зигзаг применяют, чтобы неравномерную нагрузку вторичных обмоток распределить между фазами первичной сети [1] и для получения требуемых фазовых сдвигов в многопульсных схемах выпрямления. На рис. 2.36 показано соединение обмоток звезда – зигзаг и векторная диаграмма напряжений. Видно, что между напряжениями первичной и вторичной обмоток в одноимённых фазах появился фазовый сдвиг 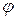, который можно изменять соотношением витков в частях вторичной обмотки. Если вторичная обмотка разделена на две равные части, то угол . 

 

 

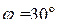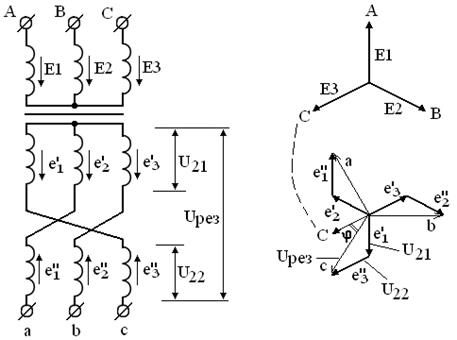
Рисунок 2.36 – Трёхфазный трансформатор при включении звезда-зигзаг

 

Трёхфазная система напряжений является симметричной, значит и магнитная система трёхфазного трансформатора должна быть симметричной, как показано на рис.2.37а. Изготовить такую магнитную систему очень сложно. Пошли по другому пути. Учитывая, что в трехфазной системе 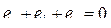, то и сумма магнитных потоков в центральном стержне . Необходимость в центральном стержне отпадает и, если сократить ярмо фазы В, то получится плоская, широко известная трёхфазная магнитная система (рис.2.37 б и рис. 2.16 г).

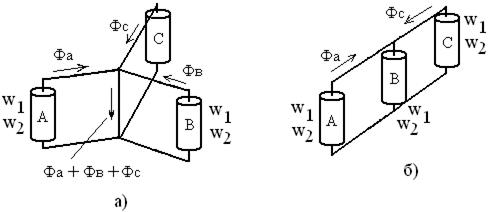
Рисунок 2.37 – Магнитная система трёхфазного

трансформатора: а) симметричная, б) несимметричная

Плоская конструкция магнитной системы высоко технологична и удобна при компоновке (размещению трансформаторов), но она в принципе является несимметричной. Вследствие различия магнитных сопротивлений для разных фаз, намагничивающие токи крайних фаз А и С больше тока средней фазы В. Это приводит к нарушению фазовых углов (они отличаются от 120 градусов). Для уменьшения магнитной асимметрии сечение верхнего и нижнего ярма делают на 10…15% больше чем стержня. Но асимметрия всё равно остаётся.

В настоящее время [10] трёхфазные трансформаторы на мощности единицы киловатт и более изготавливают с симметричной магнитной системой, но такой, как показано на рис. 2.38.

 Изготовление ярма сложности не представляет – его наматывают из стальной  ленты c помощью  оправки. Затем стержни с обмотками и оба ярма стягивают крепежом. Конструкция получилась симметричной и весьма технологичной. 

Обмотки низшего напряжения часто соединяют треугольником, так как токи в них в 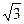 раз меньше чем линейные, а поэтому уменьшается влияние асимметрии фазных нагрузок на первичную сеть.

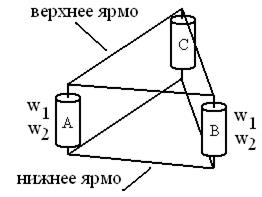
Рисунок 2.38 – Симметричная магнитная система трёхфазного

трансформатора

Импульсные трансформаторы

 Особенностью работы импульсных трансформаторов является то, что входной сигнал – однополярные импульсы и, в отличие от широкополосных  трансформаторов, сердечник работает с постоянным подмагничиванием. Рассмотрим работу импульсного трансформатора, схема включения которого приведена на рис.2.39а, а на рис 2.39б – наиболее характерные эпюры. 

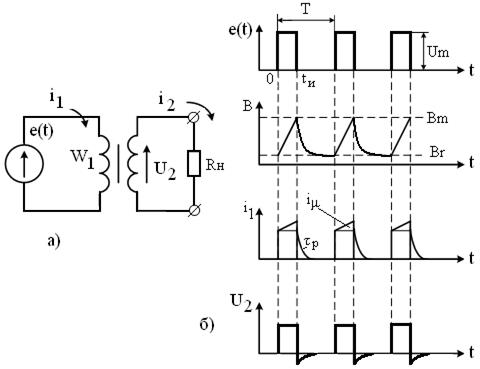
Рисунок 2.39 – Схема включения (а) и эпюры для (б) импульсного

трансформатора

Если на вход поступает сигнал е(t), то индукция линейно нарастает на интервале 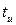 и спадает на интервале ( 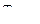) со скоростью, определяемой постоянной времени  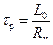 . Перепад индукции в сердечнике равен

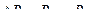                                                                                         (2.51)

Рабочая точка на петле гистерезиса перемещается по частному циклу перемагничивания, как показано на рисунке 2.40.

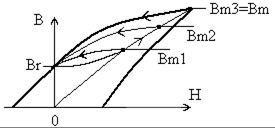
Рисунок 2.40 – Перемещение рабочей точки в сердечнике импульсного

трансформатора

Напряжение на нагрузке U₂ имеет отрицательный выброс, так как в сердечнике накапливается энергия (ток намагничивания 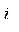). Ток первичной обмотки – трапецеидальный, поскольку  к прямоугольному току нагрузки добавляется линейный ток намагничивания сердечника.

На интервале 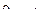 напряжение  на входе постоянно и равно . Тогда

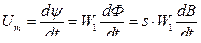                ,                                              (2.52)

где 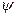 – потокосцепление

             s  – сечение магнитопровода.                                               

Так как производная неизменна, то индукция нарастает линейно. Переходим к конечным приращениям и получаем

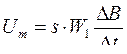                         ,                                                       (2.53)

     где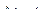    

Тогда выражение (2.53) переписываем в виде

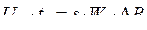                            .                                           (2.54)

Выражение (2.54) показывает площадь импульса, передаваемого в нагрузку – основной параметр импульсного трансформатора и чем она больше, тем лучше. Поэтому, чем больше перепад индукции 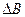, тем больше площадь импульса.

Индуктивность первичной обмотки определяется магнитной проницаемостью     

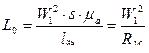                   ;                                              (2.55)

                      

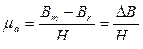
Она и определяет основную индуктивность трансформатора. Поэтому на кривой намагничивания предпочтительным является участок с максимальным μ_а. Остаточная индукция В_r должна быть возможно меньшей. Из магнитных материалов лучше всего подходят тонкие ленты трансформаторных сталей и пермаллой с малым коэффициентом прямоугольности . Реже используются ферриты, поскольку они  обладают  низкой индукцией, хотя и малыми динамическими потерями.

Примеры задач с решениями

     Пример 2.6.1

     Исходные данные:  Индукция в сердечнике трансформатора В_m =1,0 Тл, число витков первичной обмотки W₁ =1000, приложенное напряжение – меандр U₁ =100 В с частотой 1кГц.

     Определите необходимую площадь сечения магнитопровода.

     Решение. Воспользуемся  уравнением трансформаторной ЭДС  для прямоугольной формы напряжения: 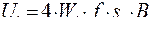. Откуда находим

        

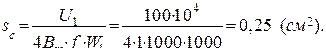
Пример 2.6.2

Исходные данные: Максимальная индукция в сердечнике из феррита равна В_m =0,38 Тл при напряженности Н = 25 А/м,  число  витков первичной обмотки  W =800, поперечное сечение магнитопровода s_с=0,19 см², средняя длина магнитной силовой линии 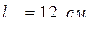, частота приложенного напряжения (меандра)  f =10 кГц,.

Определите предельные значения тока холостого хода  I₁₀ , напряжения U₁ и изобразите зависимость .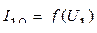

Решение.  Из уравнения трансформаторной ЭДС следует: 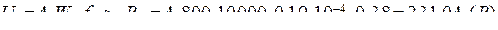. Предельное значение тока холостого хода –

.

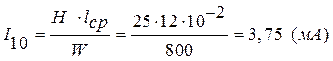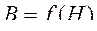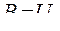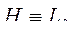Учитывая характер  и то, что , а , зависимость намагничивающего тока трансформатора от приложенного напряжения имеет примерно квадратичный характер (рисунок 2.41).

 

 

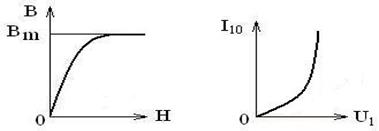
Рисунок 2.41 – Зависимость тока намагничивания от напряжения

Пример 2.6.3  

Исходные данные: Зависимость магнитного потока от времени Ф(t) показана на рисунке 2.42.

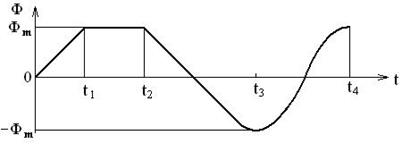
Рисунок 2.42 – Зависимость магнитного потока от времени Ф(t)

Изобразите  зависимость ЭДС от времени.

Решение.  Учитывая закон электромагнитной индукции 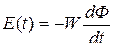, определим Е(t) раздельно по участкам. На участке [0…t₁] функция линейна и скорость (производная) постоянна: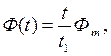 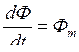. Тогда 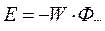. На участке [t₁…t₂] 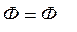поэтому 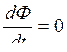. На интервале [t₂…t₃], повторяется участок [0…t₁], но с другим знаком. На участке [t₃…t₄] имеет место гармонический закон изменения потока 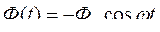, поэтому получаем ортогональную функцию. Результирующая зависимость Е(t) изображена на рисунке 2.43.

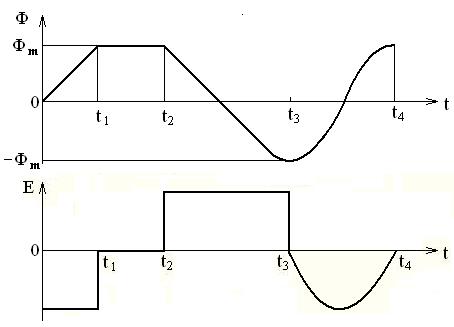
Рисунок 2.43 – Зависимость ЭДС от времени

Пример 2.6.4

     Исходные данные: ЭДС первичной обмотки трансформатора изменяется во времени, как показано на рисунке 2.44.

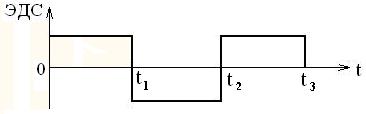
Рисунок 2.44 – Зависимость ЭДС от времени

 

Изобразите  временную зависимость магнитного потока Ф(t).

Решение.  Согласно закону электромагнитной индукции 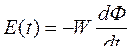   для конечных приращений  находим: 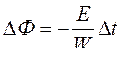. На участке [t₀…t₁] с учётом знака ЭДС, график будет убывающим. Таким образом, кривая магнитного потока Ф(t) имеет вид, как показано на рисунке 2.45.  

 

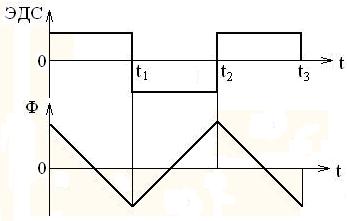
Рисунок 2.45 –Зависимость магнитного потока от времени 

 

Пример 2.6.5.

 Исходные данные: В однофазном трансформаторе при КПД=0,95  и  коэффициенте загрузки 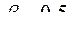, выходная мощность  P₂ =190 Вт. 

   Определите потери в обмотках.

Решение. КПД трансформатора 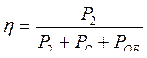. При оптимальном коэффициенте загрузки,  P_C = P_ОБ (рис.2.28). Решим относительно Р_ОБ.

 

Следовательно,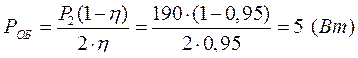

Пример 2.6.6

Исходные данные: В результате проведения опыта короткого замыкания трансформатора с  отношением витков W₁/W₂=5, найдено Rкз = 10 Ом.

Определите сопротивления потерь первичной и вторичной обмоток.

Решение.  Схема замещения трансформатора в опыте КЗ имеет вид, как показано на рисунке 2.46.

 

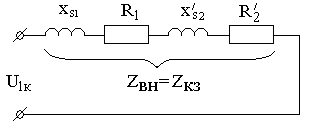
Рисунок 2.46 – Схема замещения трансформатора в опыте КЗ

 

Из определения коэффициента трансформации следует, что   W₁/W₂= n=5.

В оптимальном трансформаторе  имеет место: 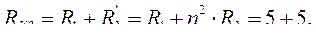 Следовательно, .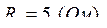

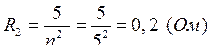Пример 2.6.7

 Исходные данные: В схеме замещения трансформатора (рисунок 2.47) имеет место U_1ном=141В, U_кз=10%, , .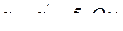

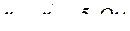Определите номинальный ток первичной обмотки трансформатора.

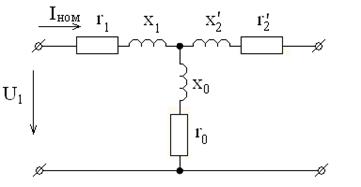
Рисунок 2.47 – Схема замещения трансформатора

Решение. Определим внутреннее сопротивление трансформатора:

, , .

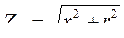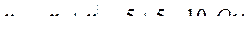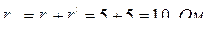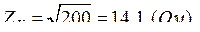
В опыте КЗ на вход подаётся пониженное напряжение: . Тогда номинальный ток равен .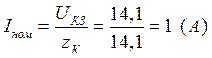

Пример 2.6.8

     Исходные данные: Трансформатор выполнен на броневом сердечнике (рисунок 2.48). Все обмотки равны W₁=W₂=W₃. К обмотке W₁ подведено напряжение U₁=100В.

Определите напряжения  U₂ и U₃._.

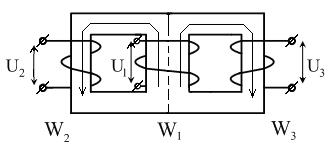
Рисунок 2.48 – Трансформатор

 

Решение. В сердечнике трансформатора основной магнитный поток делится на две части, которые пронизывают свои обмотки W₂ и W₃. Из уравнения  трансформаторной ЭДС: 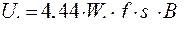 следует, что основной магнитный поток прямо пропорционален напряжению, следовательно,  U₂ =U₃ =

= 50 В.

Пример 2.6.9

Исходные данные: В стержневой однофазный трансформатор (рисунок 2.49) вводится магнитный шунт.

Определите как изменится выходное напряжение трансформатора (U₂)  на холостом ходу при введении магнитного шунта.

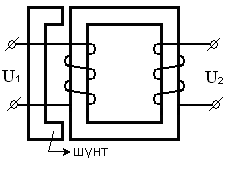
Рисунок 2.49 – Введение магнитного шунта

Решение.  Вследствие введения магнитного шунта, появляется ещё один путь для магнитного потока (см. рисунок 2.50), что приведёт к уменьшению потока Ф ₀ и уменьшению напряжения U₂  пропорционально магнитным сопротивлениям.

 

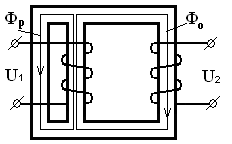
Рисунок 2.50 – Влияние магнитного шунта

Пример 2.6.10

Исходные данные: Потери в магнитопроводе  трансформатора составляют Pст = 10 Вт; соотношение витков –  W1/W2= 1; активные сопротивления обмоток  r₁ =  r₂  = 0,2 Ом.

Определите при каком токе нагрузки I₂  КПД трансформатора будет максимальным?

Решение. КПД трансформатора максимален, когда Р_СТ =Р_ОБ . Коэффициент трансформации n=1. Поэтому Р_СТ =I₂²*r_к , где 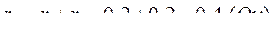. Тогда .

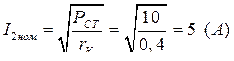Пример 2.6.11

Исходные данные: Из опыта холостого хода трансформатора получено:  U₁хx=220В; I₁xx=0,4A; P₁xx=16Вт.

Определите активное сопротивление цепи намагничивания в схеме замещения трансформатора.

Решение. В опыте холостого хода схема замещения трансформатора имеет вид (рисунок 2.51):

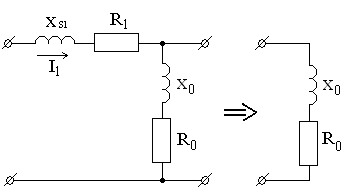
Рисунок 2.51 – Схема замещения трансформатора в опыте ХХ

 

Пренебрегая потерями и индуктивностью рассеяния, получим

                               .

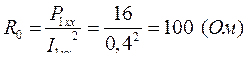Пример 2.6.12

Исходные данные: В трансформаторе при питании от сети с напряжением 220 В и частотой сети f=50 Гц потери в магнитопроводе  составляют Р_СТ =20 Вт.

Определите потери в магнитопроводе, если этот трансформатор включить в сеть с частотой 400 Гц и напряжением 110 В (зависимость потерь от частоты и индукции принять квадратичной).

Решение.  Магнитная индукция пропорциональна напряжению, а потери зависят от индукции и частоты согласно выражению (2.2)  . Следовательно,

Пример 2.6.13

Исходные данные: Первичная обмотка трёхфазного трансформатора соединена звездой.

Определите во  сколько раз изменятся потери в магнитопроводе, если первичную обмотку трёхфазного трансформатора переключить на треугольник.

Решение.  При соединении обмоток треугольником  к каждой фазной обмотке трансформатора прикладывается линейное напряжение (U_л), которое больше фазного (Uф) в 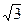 раз. 

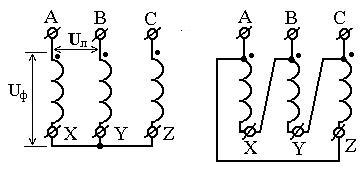
Рисунок 2.52 – Схема соединения обмоток  звездой и треугольником

  

Потери в магнитопроводе зависят от индукции и частоты согласно выражению (2.2 )         .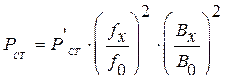

При переходе на соединение треугольником напряжение, прикладываемое к фазной обмотке  увеличивается в 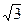 раз, что приведёт к увеличению  магнитной индукции в  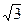раз, а потери возрастут в 3 раза.    

Выпрямители и фильтры

3.1 Преобразование переменного тока в постоянный

     Выпрямитель – устройство, преобразующее напряжение переменного тока в напряжение постоянного тока. Это устройство нелинейное, поскольку преобразуется спектр сигнала. На рис.3.1 показано условное изображение выпрямителя (преобразователя AC/DC), а также временные и спектральные характеристики входного (U₁)  и выходного (U_d) напряжений.

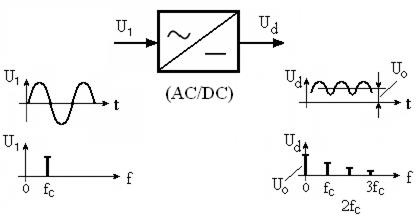
Рисунок 3.1 –  Условное изображение выпрямителя (AC/DC) и

характеристики входного и выходного напряжений.

 

Задача выпрямителя – перенести энергию сигнала U₁ с частоты сети f_c на постоянную составляющую – сигнал U_0.

 Задача фильтра, подключаемого к выходу выпрямителя – выделить только постоянную составляющую U₀ (полезный эффект выпрямления ) и отфильтровать все остальные гармоники (пульсации) напряжения U_d, то есть “сгладить” напряжение. Такой фильтр называется сглаживающим и представляет собой ФНЧ с полосой пропускания << .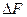

Если выпрямитель использует одну полуволну напряжения переменного тока, то он называется однотактным (однополупериодным), если обе полуволны – двухтактным (двухполупериодным).

Однотактное выпрямление ( преобразование) иллюстрируется схемой и эпюрами рис.3.2 Ключ К синхронно с частотой источника U₁ подключает нагрузку к источнику на время одной полуволны (T/2). Если напряжение гармоническое , то на нагрузке получается пульсирующее напряжение с частотой . За период через нагрузку и источник проходит только один импульс тока. Частота первой гармоники тока (и напряжения пульсаций на нагрузке) равна частоте сети . Постоянная составляющая тока нагрузки протекает и через источник, вызывая его постоянное подмагничивание.

 

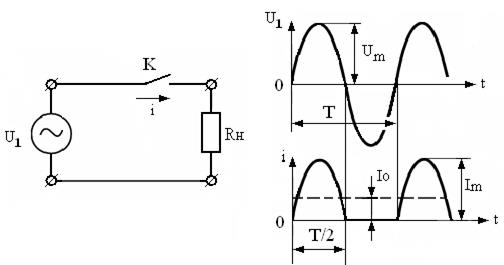
Рисунок 3.2 – Однотактное выпрямление

 

Двухтактное выпрямление (преобразование) иллюстрируется схемой и эпюрами рис.3.3. Ключи К1 и К2 синхронно с частотой источника U₁ подключают нагрузку на время одной полуволны (Т/2) два раза за период.

 

 

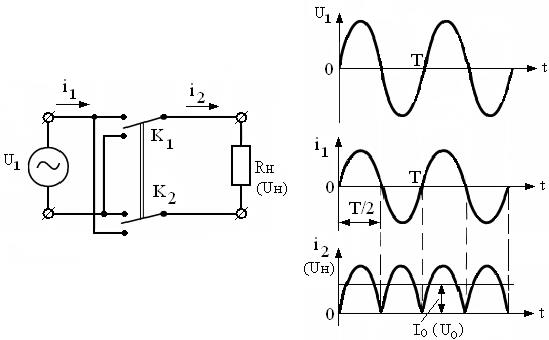
Рисунок 3.3 – Двухтактное выпрямление

 

Поэтому за период сети через нагрузку и источник проходят два импульса тока, причем через нагрузку – в одном направлении, а через источник – в противоположных направлениях. Частота импульсов тока (напряжения U_H) в нагрузке в два раза выше частоты сети ( ). Постоянная составляющая тока нагрузки не протекает через первичный источник и не влияет на его работу. В этом состоит основное отличие двухтактного выпрямления от однотактного.

Суть выпрямления переменного тока (принцип построения выпрямительных устройств) состоит в том, что через источник ток может протекать в одном или двух направлениях, а через нагрузку – только в одном направлении.

В качестве ключей для схем выпрямления используются неуправляемые и управляемые вентили (диоды, тиристоры, биполярные и полевые транзисторы). Наиболее широко известны неуправляемые вентили – диоды.