3.1. Простейшие тригонометрические уравнения.
Определение: Уравнение называется тригонометрическим, если оно содержит переменную только под знаками тригонометрических функций.
Определение: Решить тригонометрическое уравнение – значит найти все действительные числа, обращающие уравнение в тождество, или доказать что их нет.
Пример: Решить уравнение: cos х – sin х = 0.
Решение: Данное уравнение равносильно уравнению cos х = sin х .
Углы, радианные меры которых удовлетворяют этому уравнению, могут находиться в первой и третьей координатных четвертях, так как синус и косинус имеют в них одинаковые знаки. Синус и косинус имеют одинаковые значения при углах х =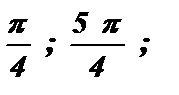 
… или х = 
.
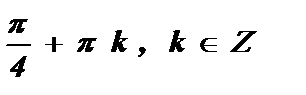Ответ: х = .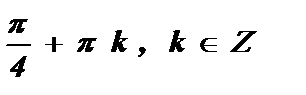
Определение: Простейшие тригонометрические уравнения - это уравнения вида: sin х = а , cos х = а , tg х = а , ctg х = а , где
а – данное действительное число.
Замечание: Решение любого тригонометрического уравнения сводится к решению простейших тригонометрических уравнений .
Так как тригонометрические функции являются периодическими функциями, достаточно найти корни уравнений на отрезке длиной равной основному периоду тригонометрической функции.
sin х = а
1. а > 1 , а < – 1 , sin х = а корней нет.
2. а = 1 , sin х = 1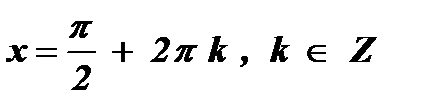 
.
3. а = 0 , sin х = 0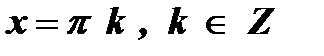 
.
4. а = – 1 , sin х = – 1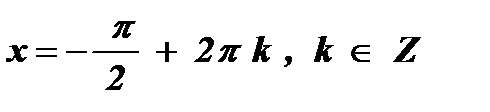 
.
5. – 1 < а < 1 , sin х = а х 1 = arcsin а + 2 p k , k Î Z
х 2 = p – arcsin а + 2 p k , k Î Z .
Или
х 1,2 = ( – 1 ) к · arcsin а + p k , k Î Z .
Пример: Решить уравнения:
№1. sin 3х = – 1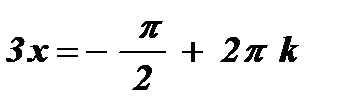 
.
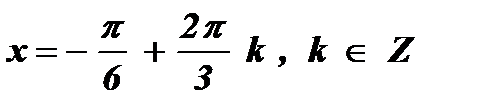№2. sin ( 2х –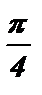 
) = 0 2х – 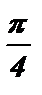= p k 2х = 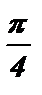+ p k 
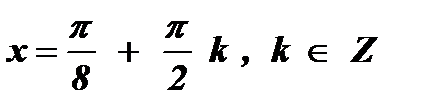
№3. sin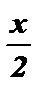 
= 
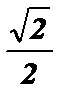
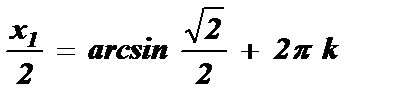
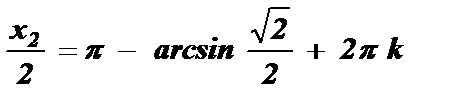
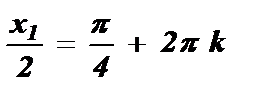
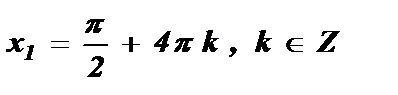
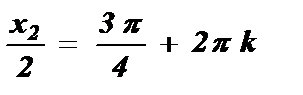
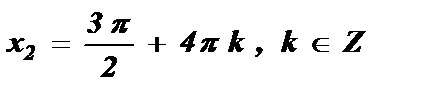
Ответ: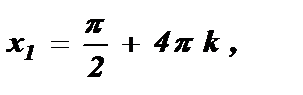 
.
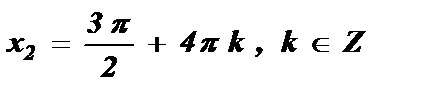cos х = а
1. а > 1 , а < – 1 , cos х = а корней нет .
2. а = 1 , cos х = 1 х =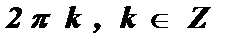 
.
3. а = 0 , cos х = 0 х =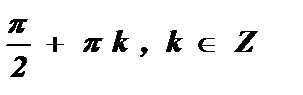 
.
4. а = – 1 , cos х = – 1 х =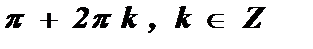 
.
5. – 1 < а < 1 , cos х = а х 1 = arccos а + 2 p k , k Î Z
х 2 = – arccos а + 2 p k , k Î Z .
Или
х 1,2 = ± arccos а + 2 p k , k Î Z .
Пример: Решить уравнения:
№1. cos ( 3х –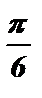 
) = 1 3х – 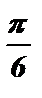= 2 p k 3х = 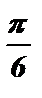+ 2 p k х = 
.
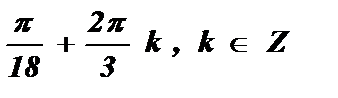№2. cos ( х –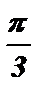 
) = 
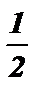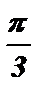х1 – = arccos 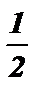+ 2 p k х2 – 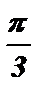= – arccos 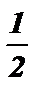+ 2 p k
х1 – 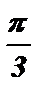= 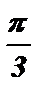+ 2 p k х2 – 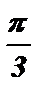= – 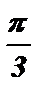+ 2 p k
х1 = 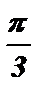+ + 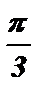2 p k х2 = – 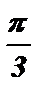+ + 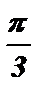2 p k
х1 =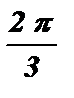 
+ 2 p k , k Î Z . х2 = 2 p k , k Î Z .
Ответ: х1 = 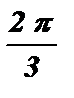+ 2 p k , х2 = 2 p k , k Î Z .
№3. cos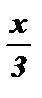 
= 
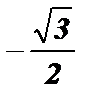
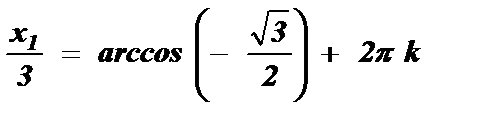
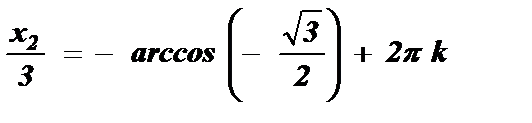
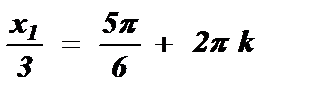
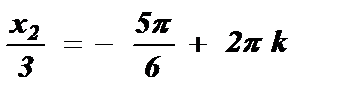
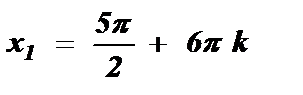, k Î Z 
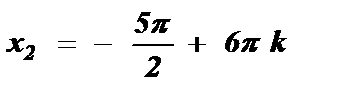, k Î Z .
Ответ: 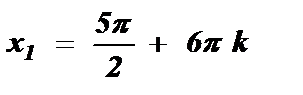, , 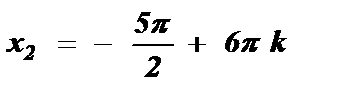k Î Z .
tg х = а , а - любое число, х = arctg а + p k , k Î Z
ctg х = а , а - любое число, х = arcс tg а + p k , k Î Z
Пример:
№1. tg 2х =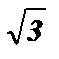 
2х = arctg 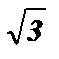+ p k 2х =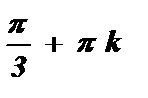 
.
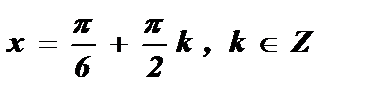№2. с tg 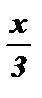= 7 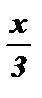= arcс tg 7 + p k x = 3 arcс tg 7 + 3 p k , k Î Z .
№3. с tg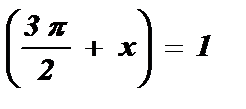 
tg x = - 1 x = arctg ( - 1 ) + p k x = 
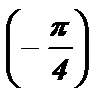+ p k , k Î Z .
3.2.Тригонометрические уравнения, приводимые к квадратному.
Замечание: При решении тригонометрических уравнений целого вида, содержащих синусы и косинусы, область допустимых значений не устанавливается, так как эти функции определены для любого действительного значения.
Пример №1: Решить уравнение: 8 sin 2 x - 6 sin x - 5 = 0 .
Решение:
Введем новую переменную у = sin x , получим квадратное уравнение:
8 у 2 - 6 у - 5 = 0; D = b 2 - 4 ac; D = ( - 6 )2 - 4 · 8 · ( - 5 ) = 196;
; 
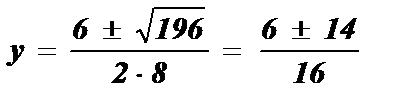; y 1 = 
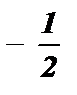; y 2 = 
;
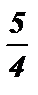sin x = 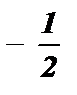; х 1,2 = ( – 1 ) к · arcsin 
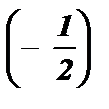+ p k ; х 1,2 = ( – 1 ) к · 
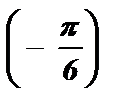+ p k ;
х 1,2 = ( – 1 ) к+1 ·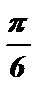 
+ p k , k Î Z ;
sin x = 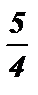корней нет , так как - 1 £ sin x £ 1 .
Ответ: х 1,2 = ( – 1 ) к+1 · 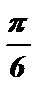+ p k , k Î Z .
Пример №2: Решить уравнение: 8 sin 2 3 x + 6 cos 3 x - 3 = 0 .
Решение:
Используя формулу cos 2 3x + sin 2 3x = 1 , заменим sin 2 3x = 1 - cos 2 3x .
8 (1 - cos 2 3x ) + 6 cos 3x - 3 = 0; 8 - 8 cos 2 3x + 6 cos 3x - 3 = 0;
- 8 cos 2 3x + 6 cos 3x + 5 = 0; 8 cos 2 3x - 6 cos 3x - 5 = 0;
Введем новую переменную у = cos 3 x , получим квадратное уравнение:
8 у 2 - 6 у - 5 = 0; D = b 2 - 4 ac; D = ( - 6 )2 - 4 · 8 · ( - 5 ) = 196;
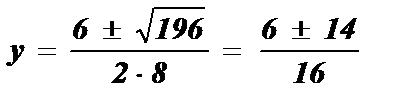; ; y1 = 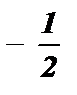; y2 = ;
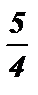cos 3x = 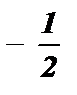; 3х = ± arccos 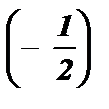+ 2 p k ; 3х = ± 
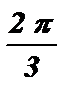+ 2 p k ;
.
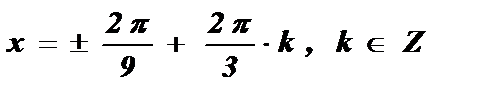cos 3 x = 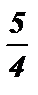корней нет , так как - 1 £ cos 3 x £ 1 .
Ответ: .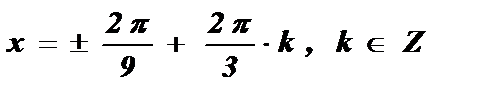
Пример №3: Решить уравнение: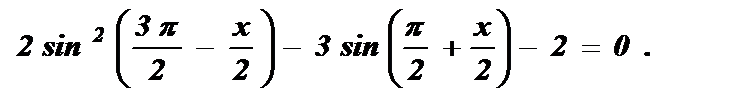 
Решение:
Воспользуемся формулами приведения:
; 
;
; 
;
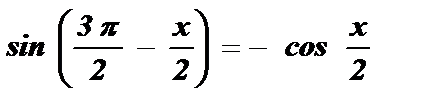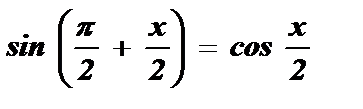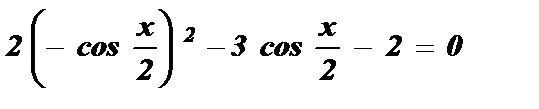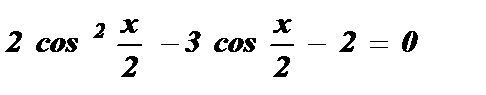Введем новую переменную у = cos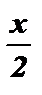 
, получим квадратное уравнение:
2 y 2 - 3 y - 2 = 0; D = b 2 - 4ac; D = ( - 3 )2 - 4 · 2 · ( - 2 ) = 25;
; 
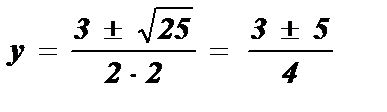; y1 = 
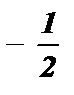; y2 = 2;
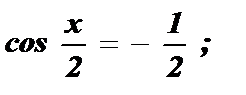
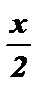= ± arccos 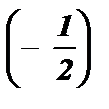+ 2 p k ; 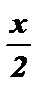= ± 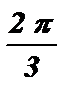+ 2 p k ;
x = ±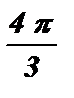 
+ 4 p k , k Î Z .
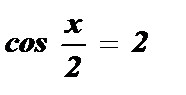корней нет , так как - 1 £ cos 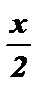£ 1 .
Ответ: x = ± 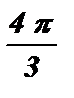+ 4 p k , k Î Z .
Пример №4: Решить уравнение: 3 cos 2 x = 7 sin x .
Решение:
Воспользуемся формулой cos 2x = 1 - 2 sin 2 x :
3 ( 1 - 2 sin 2 x ) - 7 sin x = 0; 3 - 6 sin 2 x - 7 sin x = 0;
Введем новую переменную у = sin x , получим квадратное уравнение:
- 6 y 2 - 7 y + 3 = 0; 6 y 2 + 7 y - 3 = 0; D = b 2 - 4ac; D = 7 2 - 4 · 6 · ( - 3 ) = 121;
; 
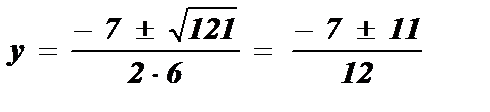; y1 = 
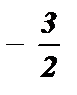; y2 = 
;
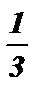sin x = 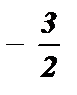корней нет , так как - 1 £ sin x £ 1 .
sin x = 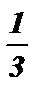х 1,2 = ( – 1 ) к · arcsin 
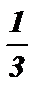+ p k , k Î Z .
Ответ: х 1,2 = ( – 1 ) к · arcsin 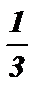+ p k , k Î Z .
3. 3. Однородные тригонометрические уравнения.
Определение: Тригонометрическое уравнение вида a sin x + b cos x = 0
( a Î R , b Î R , a ¹ 0 , b ¹ 0 ) называется однородным первой степени относительно sin x и cos x .
Определение: Тригонометрическое уравнение вида a sin 2 x + b sin x cos x + с cos 2 x = 0
( a Î R , b Î R , с Î R , a ¹ 0 , b ¹ 0 , с ¹ 0 ) называется однородным второй степени относительно sin x и cos x .
Способ решения: Значения аргумента х, при которых sin x = 0 или cos x = 0 , не являются корнями тригонометрического уравнения однородного n-ой
степени относительно sin x и cos x , так как если sin x = 0
(cos x = 0), то из данного уравнения следует равенство cos x = 0
(sin x = 0), а из основного тригонометрического тождества следует, что косинус и синус не могут быть одновременно равными нулю. Поэтому чтобы решить тригонометрическое уравнение однородное n-ой степени относительно sin x и cos x , можно обе части уравнения разделить на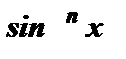 
или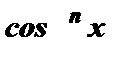 
.
Пример №1: Решить уравнение: sin x + 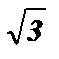cos x = 0 .
Решение:
Данное тригонометрическое уравнение является однородным первой степени относительно sin x и cos x .
Разделим обе части этого уравнения на cos x ¹ 0, получим:
tg x + 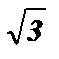= 0 ; tg x = 
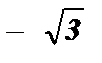; x = arctg ( 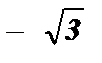) + p k ; x = 
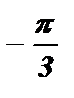+ p k , k Î Z .
Ответ: x = 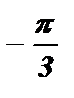+ p k , k Î Z .
Пример №2: Решить уравнение: 5 sin 2 x + 3 cos 2 x = 4 sin 2 x .
Решение:
Воспользуемся формулой sin 2 x = 2 sin x cos x :
5 sin 2 x + 3 cos 2 x - 8 sin x cos x = 0 ;
Полученное тригонометрическое уравнение является однородным второй степени относительно sin x и cos x . Разделим обе части этого уравнения на cos 2 x ¹ 0, получим: 5 tg 2 x - 8 tg x + 3 = 0;
Введем новую переменную у = tg x , получим квадратное уравнение:
5 y 2 - 8 y + 3 = 0; D = b 2 - 4ac; D = ( - 8 ) 2 - 4 · 5 · 3 = 4;
; 
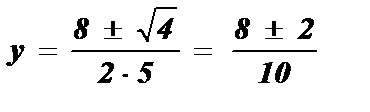; y1 = 
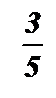; y2 = 1 ;
tg x = 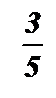; x = arctg 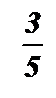+ p k , k Î Z .
tg x = 1 ; x = arctg 1 + p k ; x = 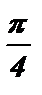+ p k , k Î Z .
Ответ : x = arctg 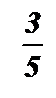+ p k , x = 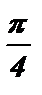+ p k , k Î Z .
Пример №3: Решить уравнение: 3 sin 2 x - 4 sin x cos x + 5 sin 2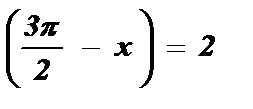 
.
Решение:
Воспользуемся формулой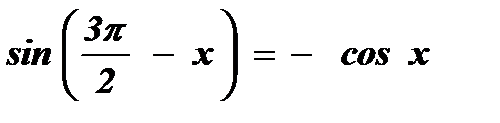 
.
C помощью формулы sin 2 x + cos 2 x = 1 выполним замену
2 = 2 ·1 = 2 (sin 2 x + cos 2 x ) .
3 sin 2 x - 4 sin x cos x + 5 ( - cos x ) 2 = 2 (sin 2 x + cos 2 x );
3 sin 2 x - 4 sin x cos x + 5 cos 2 x - 2 sin 2 x - 2 cos 2 x = 0;
sin 2 x - 4 sin x cos x + 3 cos 2 x = 0;
Дата: 2018-12-21, просмотров: 432.
